The Shanghai Tower Is The Tallest In China. But The Chinese Are Flocking To It For Another Reason
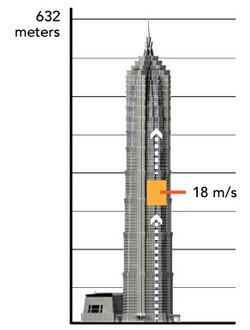 The Shanghai Tower is the second tallest in the world, and has an architectural height of 632 meters. It is equipped with the world’s fastest elevator, which can travel at 18 m/s. Several newspapers reported that it will reach the top in just under 36 seconds, which isn't true due to physical limitations.
The Shanghai Tower is the second tallest in the world, and has an architectural height of 632 meters. It is equipped with the world’s fastest elevator, which can travel at 18 m/s. Several newspapers reported that it will reach the top in just under 36 seconds, which isn't true due to physical limitations.
Firstly, the top floor of the building is only 557 meters high. Secondly, in order to prevent accidents to pregnant women, the maximum allowed acceleration is 1.25 m/s 2 . Thirdly, for passenger comfort, the maximum jerk (rate of change of acceleration) is 2.50 m/s 3 .
Based on these measurements, what is the shortest time that it would take an elevator to reach the top floor?
Details and assumptions
It actually takes the elevator 55 seconds to ascend 565 meters, due to further physical limitations. You can read more in the Mitsubishi Elevator Technical Paper .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
When you reach the max speed of 18m/s, your accelleration still must decrease from its max (1.25m/s^2) to 0. But you can't slow down immediately. The accelleration also needs 0.5s because of the same max jerk that caused the 0.5s at the very start. So there is only 13.9s to reach max speed and still reduce the accelleration. This happens also (mirrored) near the end. With this I get 45.8618s.
Log in to reply
A friend of mine showed a still better answer.
The accelleration graphic is: linear ramp up+horizontal at max 1 . 2 5 m / s 2 followed by a linear ramp down until reaching the (constant) max speed of 18m/s. Each ramp durates 0.5 seconds with a max jerk of ( + o r − ) 2 . 5 m / s 3 . Both ramps can be combined so that the total area beneath the accelleration graphic (= total gained speed) is identical to a constant accelleration at max speed with duration 0.5s more.
The duration is 1 . 2 5 m / s 2 1 8 m / s = 1 4 . 4 s . Including the jerk, the duration will then be: 1 4 . 4 + 0 . 5 = 1 4 . 9 s .
The accelleration graphic (from zero to start of max speed) is symmetrical, thus the mean speed in this traject is 18/2 or 9m/s.
A similar approach holds for the deceleration near the top floor. Distance risen during both accelleration and deceleration is then 9 ∗ 1 4 . 9 ∗ 2 = 2 6 8 . 2 m . This leaves 5 5 7 − 2 6 8 . 2 = 2 8 7 . 8 m to rise with constant (max) speed, taking 2 8 7 . 8 / 1 8 = 1 6 . 0 0 4 4 4 s . Total time is then 1 4 . 9 + 1 6 . 0 0 4 4 4 + 1 4 . 9 = 4 5 . 8 0 4 4 4 s .
With thanks to Erwin van Beek.
Log in to reply
But, like I said on previous comment: During the 'jerk' works the speed also increase/ decrease and also there is a distance that's covered by elevator during that process. Luckily, the time taken for the jerk works only 0 . 5 s , if more than that your solution seems flaw.
Log in to reply
@Tunk-Fey Ariawan – I don't see the flaw. The jerk works 4 times 0.5s: to start accelleration, to stop accelleration at max speed, to start deceleration and to stop deceleration.
During jerk nr 1 and 2, the accelleration increases, resp. decreases linearly from 0 to max 1.25m/s^2 resp from 1.25m/s^2 to 0. Both jerk nr 1 and 2 amount to the same increase of speed. Added together, the jerks nrs 1 and 2 amount to exactly the same increase of speed as if you had 0.5s of constant max accelleration, instead of 0.5s of linear increase of accelleration + 0.5s of linear decrease of accelleration. If you draw the graph of the accelleration during jerk nr 1and 2, you see that the areas beneath the two triangles are mirrorred.
Something similar happens during jerks nrs 3 and 4.
You also should consider that while 'jerk' works the speed also increased/ decreased & there is a distance that's covered by elevator during that process. I solve this problem using 7 frames of time from elevator starts to move until rest at the top.
Hi Tunk-Fey, I did consider that while 'jerk' works, the speed also increased/decreased & there is a distance that's covered by elevator during that process.
Let's see when the 'jerk' works in (your) frames. These are frames 1, 3, 5 and 7. Let's see what happens in frames 1 and 3. (A similar argument will hold for frames 5 and 7).
While the 'jerk' works in frame 1 to get the acceleration at its highest as fast as possible, it takes 0.5 seconds. With that acceleration, the speed is not yet at its max. Otherwise the 'jerk' should have stopped sooner to prevent passing the max speed, and consequently the max acceleration wouldn't have been reached. The max speed will be reached nearly in frame 2 and exactly at the end of frame 3, this is because the jerk will work to reduce the acceleration neatly.
Now, we don't know (yet) how much distance the elevator has covered during this 'jerk' at work, but we know this: the time spent is 0.5 seconds in frame 1 (and also 0.5 s in frame 3), the acceleration has increased (decreased) linear and the speed has decreased progressively in frame 1 (degressively in frame 3). Now you can calculate the distance covered during this 0.5 seconds in frames 1 and 3 (identical to the distance covered in frames 5 and 7), but this is not necessary.
Let's see what happens in frames 1 and 3 exactly: = 'jerk': frame 1 has constant +2.5 m/s^3; frame 3 has constant -2.5 m/s^3 = acceleration: frame 1 increases linear from 0 to its max at 1.25 m/s^2; frame 3 decreases linear from its max at 1.25 m/s^2 = speed: frame 1 increases from 0 to some speed X; frame 3 increases from some speed Y to its max of 18 m/s. The 'problem' is that the graphic is convex (concave).
Now the interesting part, learned from my friend Erwin, is that we don't need to calculate the X and Y (and subsequently the involved distances). Notice that X equals the area in the 'acceleration-graphic' during frame 1. And Y is equal to the area in the 'acceleration-graphic' during frames 1 and 2. The total speed / total area during framed 1, 2 and 3 is 18 m/s. The surprising thing is that, since the acceleration is linear during frames 1 and 3, that X is equal to the speed increase during frame 3, or X = 1 8 m / s − Y .
If we want to know what X (or 18-Y) is, we can calculate, but, again, we don't have to. What suffices is that X (and 18-Y) equals the area beneath the acceleration graphic, which is a triangle (idem for 18-Y). And both triangles can be combined in one square: a constant acceleration during 0.5 seconds will amount to the same increase of speed and amount to the same amount of distance covered as 0.5 s in frame 1 + 0.5 s in frame 3. So, we make the calculation much easier. In other words: the distance and time covered with 'jerk' at work is computationally equivalent to the distance and time covered when removing the jerk, acceleration instantly at maximum 1.25 m/s^2 and instantly at 0 when the maximum speed is reached, albeit with 0.5 s less.
Simplifying like this, we get a 'speed-graphic' that is now linear also. So we can compute the mean speed, and have to correct the 0.5 seconds to go back to the situation where 'jerk' is at work.
So, my calculation is exact and not an approximation.
Log in to reply
Hi Mr. Ron Van den Burg, I've checked your approach to solve this problem and I admit it that there is no wrong in it and your solution, also your friend of course, is simpler than mine. It never crossed in my mind to solve this problem by using graphical method like you did, instead I used calculus (integration) method which I found it was very complicated. I apologize to you for my mistake.
Log in to reply
There is nothing to apologise. Also, you made no mistake. Your calculus was correct. My explanation was just too terse. You just thought that I 'forgot' to take the jerk into account. Thanks to your comment, I realised that my comment wasn't clear enough. Thank you for commenting.
we don't know if ω² is equaled to x² because it's actually just s². So. 5 - s²(x - 1)(x + 2).
The most efficient motion for the elevator is to use maximum jerk for some period of time (say, a seconds) to get up to maximum acceleration. Then, maintain this maximum acceleration for some period of time (say b seconds) until the elevator is almost at maximum speed, and then use maximum negative jerk to reduce to zero acceleration as the elevator hits top speed. Then, maintain this top speed for some period of time (say c seconds) until the elevator is approaching the top, at which time repeat the process in reverse.
This suggests that the jerk function will be a piecewise constant function. J ( x ) = ⎩ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎧ 2 . 5 , 0 , − 2 . 5 , 0 , − 2 . 5 , 0 , 2 . 5 , 0 , for for for for for for for otherwise 0 ≤ a ≤ a + b ≤ 2 a + b ≤ 2 a + b + c ≤ 3 a + b + c ≤ 3 a + 2 b + c ≤ x x x x x x x < a < a + b < 2 a + b < 2 a + b + c < 3 a + b + c < 3 a + 2 b + c < 4 a + 2 b + c where a , b , c are positive constants to be determined. The limitations on the elevator can be expressed as the following system of equations: A ( x ) V ( x ) D ( x ) ∣ A ( x ) ∣ ∣ V ( x ) ∣ ∣ D ( x ) ∣ = ∫ J ( x ) d x = ∫ A ( x ) d x = ∬ J ( x ) d x = ∫ V ( x ) d x = ∭ J ( x ) d x ≤ 1 . 2 5 ≤ 1 8 ≤ 5 5 7 This is a straightforward, if very tedious, system of equations to solve, with 3 equations in 3 unknowns. Doing this by hand is arduous, but a CAS or similar can do this easily, yielding the required solution.
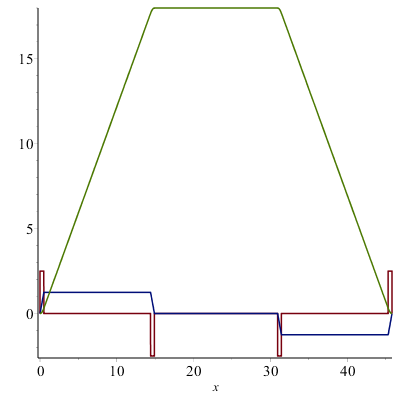
Here's a plot of the jerk (red), acceleration (blue), and velocity (green). Note that the velocity is actually continuously differentiable and has subtle curves instead of sharp edges.
 Here's a plot of the elevator's displacement.
Here's a plot of the elevator's displacement.
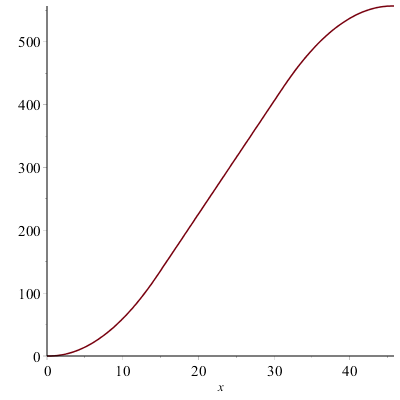 The answer to the problem is simply the value of
x
for which the maximum displacement is achieved, which is
4
5
2
0
6
3
≈
4
5
.
8
.
The answer to the problem is simply the value of
x
for which the maximum displacement is achieved, which is
4
5
2
0
6
3
≈
4
5
.
8
.
It ll take 0.5 seconds to reach the top acceleration of 1.25. Use integral calculus to find formula for s in jerk situation ( function of time cubed). It takes another 14.15 seconds to reach the top speed of 18. Overall this process has to replicated while stopping. This will give us the time taken in this process as well as distance covered. The rest of the distance is covered at a steady speed of 18.
I used pure physics to solve this problem; this should be put somewhere in Mechanics
Ok, but once you reach the top acceleration what happens? Do you immediately set your acceleration to 0, effectively giving you infinite jerk? Shouldn't the equation of motion be required to be a smooth, continuous function?
Oh right the lift has to stop at the top floor ...I forgot all about that. No wonder I couldn't get the answer
Yeah, I was literally stuck for an hour on this problem, and then I remembered that the elevator must slow down. The time it takes for the elevator to slow down is just symmetrical to the time it takes for the elevator to reach 18m/s.
the calculations were tedious and I wanted to have my dinner.So I just clicked I would like to see others approach and was glad to say that I was right. However I would like to ask, is there a simple method to do it or we just have to go through with the drudgery. Because squares aren't pretty when decimals come into play and I would really like to know a elegant answer to this.
Take a momment to think about the 'jerk' and how it works (in both ways). The solution to this problem is reached by assuming that the elevator goes from acceleration zero to 1 . 2 5 in 0 . 5 s e c then keeps a constant acceleration of 1 . 2 5 for 1 4 . 1 5 s e c to reach it's top speed of 1 8 m / s , then stays at top speed until it's time to decelerate... this methode spits out the answer 4 5 . 8 s e c , but i think this is wrong, here is why :
After the period of constant acceleration we can't directly jump to zero acceleration once we hit the limit speed because then we wouldn't be obeing the 'jerk', so insead we should give time for the system to decrease it's acceleration (not decelarate! here we are still speeding up) from 1 . 2 5 m / s 2 to 0 m / s 2 . That would give us, from the start, a 0 . 5 s e c time to reach a distance of 0 . 1 5 6 2 5 m with a speed of 0 . 3 1 2 5 m / s , then a periode of 1 3 . 9 s e c of constant acceleration in wich we travel 1 2 0 . 7 5 6 2 5 m and reach the speed of 1 7 . 6 8 7 5 m / s , then a period of 0 . 5 s e c of negative 'jerk' that will allow the acceleration to go from 1 . 2 5 m / s 2 to 0 m / s 2 while in accord with the limitations, and the speed to hit its limit at 1 8 m / s . After this we should account for the periode of constant speed, and finally mirror the first 3 steps for the deceleration phase. This would yeld a final answer of 4 7 . 3 s e c .