Who Stays Where?
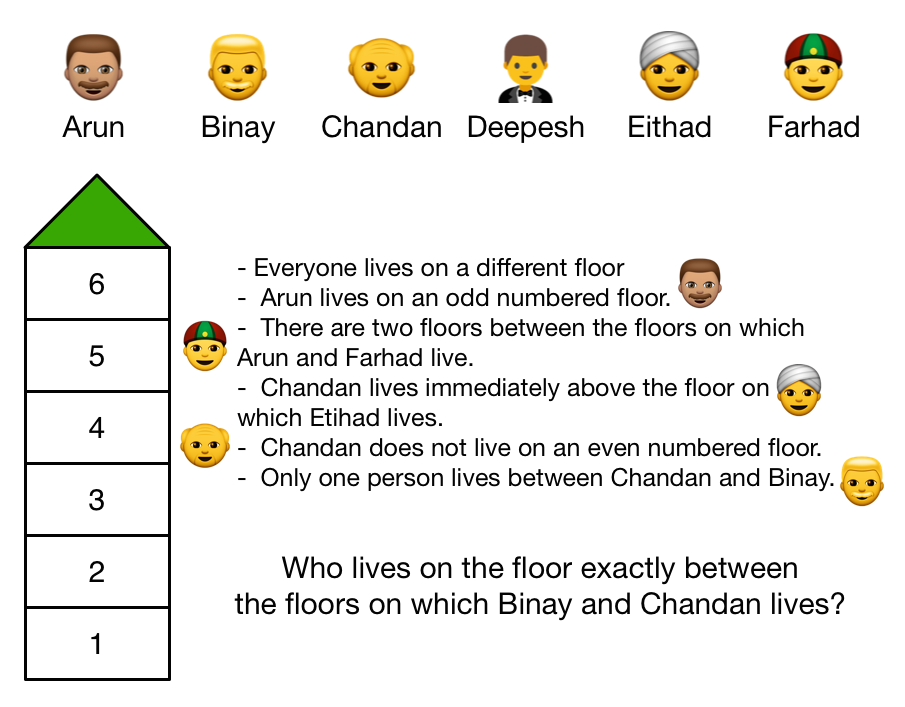
Arun, Binay, Chandan, Deepesh, Etihad and Farhad live on different floors in the Nariman Point building in Mumbai. They live on six floors numbered one to six (the ground floor is numbered 1, the floor above it, number 2 and so on and the topmost floor is numbered 6). They live according to the following conditions:
- Arun lives on an odd numbered floor.
- There are two floors between the floors on which Arun and Farhad live.
- Chandan lives immediately above the floor on which Etihad lives.
- Chandan does not live on an even numbered floor.
- Only one person lives between Chandan and Binay.
Who amongst the following lives on the floor exactly between the floors on which Binay and Chandan lives?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

Let A , B , C , D , E , F represent the floor each of the tenants (as listed) resides on. From the first and fourth conditions we know that A and C can only be one of 1 , 3 or 5 . Then from condition 5 we see that B must also be odd, (as it must differ from C by 2). So ( A , B , C ) must be some ordering of the three odd-numbered floors, but as B and C must differ by 2 we see A cannot be 3 , as this would result in B and C differing by 4. Thus the possible orderings for ( A , B , C ) are ( 1 , 3 , 5 ) , ( 1 , 5 , 3 ) , ( 5 , 1 , 3 ) and ( 5 , 3 , 1 ) .
The third condition implies that C = E + 1 , which in turn implies that C > 1 , thus eliminating ( A , B , C ) = ( 5 , 3 , 1 ) . This also means that E must be one of 2 or 4 .
The second condition implies that ∣ A − F ∣ = 3 , so since A can be one of 1 or 5 we see that F must be one of 2 or 4 . Also, since none of A , B , C , E or F can be 6 we have by default that D = 6 , (with none of the given conditions contradicting this conclusion).
We then have that ( E , F ) is one of either ( 2 , 4 ) or ( 4 , 2 ) . So, with C = E + 1 we have that ( A , B , C , D , E , F ) is one of ( 1 , 3 , 5 , 6 , 4 , 2 ) , ( 1 , 5 , 3 , 6 , 2 , 4 ) or ( 5 , 1 , 3 , 6 , 2 , 4 ) . But then as we require that ∣ A − F ∣ = 3 we are left with one possible option satisfying all the given conditions, namely ( A , B , C , D , E , F ) = ( 1 , 5 , 3 , 6 , 2 , 4 ) .
Finally, with B = 5 , C = 3 and F = 4 the person living on the floor between those occupied by Binay and Chandan is F a r h a d .