The Sunset
You are watching a beautiful sunset and decide to measure the time that the sun needs to hide itself behind the horizon. The sunset lasts Δ t = 2 min 1 7 s.
How hot is the sun's surface?

Give the result in Kelvin with 4 significant numbers.
Assumtions & Hints:
1) If you google the result, you will get the correct answer. But there is a brilliant approach to this problem.
2) It seems that some information is missing in the problem statement... but you don't need any other values! If you know that a day is 2 4 × 6 0 × 6 0 seconds and that the temperature of the Earth's surface is approximately 1 5 °C = 2 7 3 , 1 5 + 1 5 K , you should be able to solve this problem.
3) To solve this problem, you have to consider that the Earth and the Sun are black bodies. Knowing that, you can apply Stefan-Boltzmann's law : P = σ A T 4 , which gives you a relationship between radiated power P of a black body and its surface A and surface temperature T .
4) To get the exact result use Δ t = 2 min 1 6 , 7 9 6 8 s.
5) Neglect the refraction of the atmosphere (more information in the solution section)
The answer is 5778.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
I did exactly same, but my answer came 5774.9928. 😔
I already discussed the problem with you in the report section ;) You used T E a r t h = 2 8 8 K instead of T E a r t h = 2 8 8 , 1 5 K . Now I changed that in the description, sorry for that again!
I heard that refraction of the light from the sun in the atmosphere is greater at sunset and could prolong the duration of the sunset. how much of a difference would this make?
Log in to reply
Hi @Justin Travers ! Your question is pretty interesting, so I tried to "model" the refraction of the atmosphere with simple model, to give you an idea of how we could consider that.
Let's consider an atmosphere with radius R E + h and a single refraction coefficient n A . In reality, the coefficient depends on the height of the atmosphere, so we should integrate the influence of it over the height (this would complicate the problem a lot).
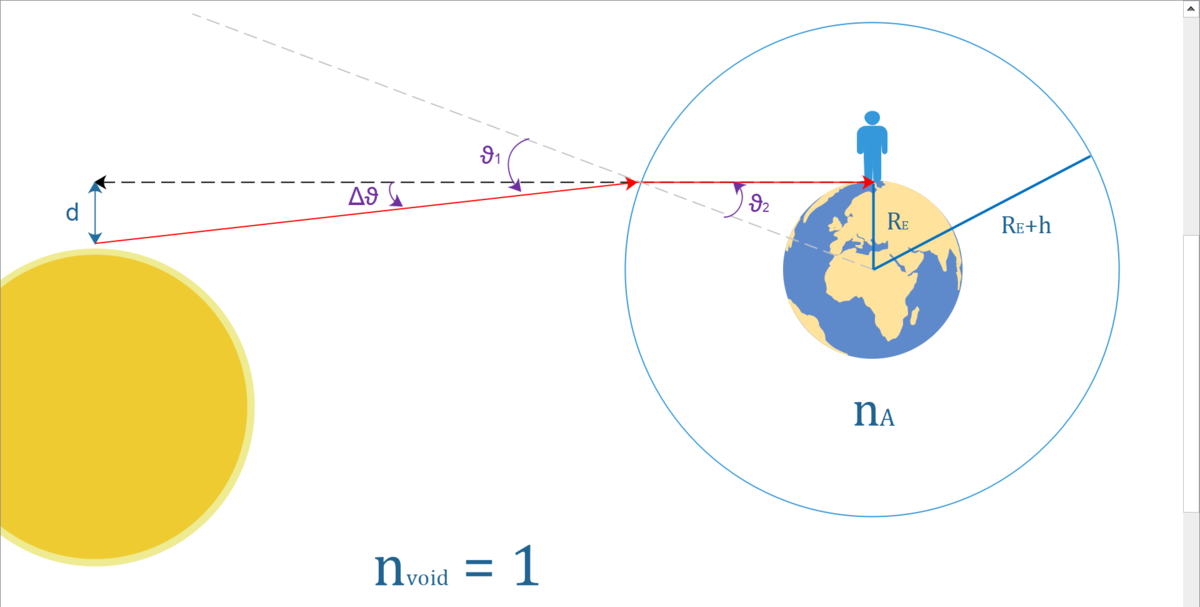
Now that we have a model and a drawing, we can use Snell's Law (https://brilliant.org/wiki/snells-law/) to relate the angle of incidence θ 1 = θ 2 + Δ θ and the angle of refraction θ 2 :
n v o i d sin θ 1 = n A sin θ 2
( n v o i d = 1 )
Using some geometry, we can determine the sine of the angle of refraction: sin θ 2 = R E + h R E . The expression simplifies to:
θ 1 = sin − 1 [ n A R E + h R E ]
...so the angle Δ θ = sin − 1 [ n A R E + h R E ] − sin − 1 [ R E + h R E ]
With this angle, we can now determine the distance of the sun under the horizon d :
d ≈ ( D E S − h ) ⋅ Δ θ ≈ D E S ⋅ Δ θ .
So back to the solution of the original problem, during the measured time Δ t the sun travelled 2 R S + d :
2 π τ Δ t = D E S 2 R S + D E S Δ θ ⟹ D E S R E = π τ Δ t − D E S Δ θ
and we get then finally for the temperature of the sun:
T S = 2 π τ Δ t − 4 1 ( sin − 1 [ n A R E + h R E ] − sin − 1 [ R E + h R E ] ) T E
I want to say it again: this is an oversimplified model, but is a good way to maybe get an estimation. If we only consider the Troposphere, then n A ≈ 1 . 0 0 0 3 and R E + h ≈ 6 3 7 0 + 1 2 km . Considering this, we get Δ θ = 5 1 0 − 3 rad and T S = 8 1 9 2 K .
Wow! This result surprised me. I am not a physicist, so I didn't expected the influence of refraction to be that big. For this problem I calculated a Δ t to get exactly T S = 5 7 7 8 K as a result. I think that a real sunset lasts more than 2 min and 17 s.
I added as an assumption to the problem that the refraction has to be neglected, even if in reality it has a big influence. Considering refraction would make this problem extremly hard ;)
If there is an error in my argumentation, I am interested in your opinions!
Log in to reply
Wow Daniel, thank you for taking my brief comment and really exploring it! I agree with you that considering refraction makes the problem hard. I don't know how to do the calculations myself. My guess is that refraction might increase the duration of the sunset slightly resulting in a slightly smaller corrected delta t. The quantity 2 Rs + d does not include the distance that refraction "moves" the sun at the start of the sunset so might overestimate the effect. Perhaps something like 2 Rs + d(end of sunset) - d(start of sunset) would be closer?
Log in to reply
@Justin Travers – You are right, this might be a better approximation. Considering this, the distances d(end) and d(start) in this simple model could even cancel out. Maybe considering a "multilayered" atmosphere to solve this problem would be a better option. This is a quite complex (and interesting) effect, unfortenatly I am not an expert in this domain. So if any astronomist reads this problem, he/she might give us a better estimate! ;)
@Justin Travers , take a look at my new problem, "the Sunrise". This problem might sound familiar to you ;)
Log in to reply
Yes, familiar! Great idea to turn it into a problem. The distance d is surprisingly large.
What is D subscript ES? Is it the radius in which the earth orbits the sun or the distance of centre of the sun from the pole Shouldn't these two distances be very different from each other?
Log in to reply
Hi @raj abhinav , Both distances are almost the same. With D E S I meant "Distance earth-sun". The radius of the Earth is neglectable compared to the distance between both bodies, so the distance earth-sun ist almost equal to the distance sun-'earth's pole'. You can check that with some pythagorean geometry:
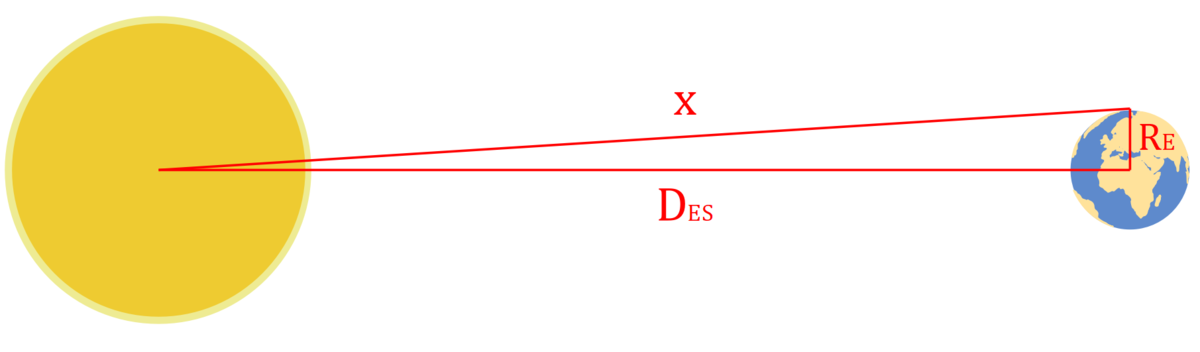
Where x is equal to the distance from the pole to the sun. Pythagoras tells us that: x 2 = D E S 2 + R E 2 . But R E = 6 , 3 7 1 ⋅ 1 0 3 km while D E S = 1 4 9 , 6 0 ⋅ 1 0 6 km So x 2 ≈ D E S 2 .
I hope this answers your question! If I missunderstood you, let me know.
Log in to reply
Thanks for clarifying. I appreciate your work, but the result you got when in the reply to JUSTIN TRAVERS isn't digestible to me. Also I am not a physicist but if you have some clue what could have went wrong in your beautiful way of modelling the refractive index addition to the problem please let me know.
Log in to reply
@Raj Abhinav – Hi Raj, I didn't saw your question! I think that nothing went "wrong" in my argumentation, but the approach I took to model the atmosphere was too simple. On the one hand, in reality the refraction coefficient changes over the height, so you should do some complicated calculus, to maybe get a better result. On the other hand, I hadn't considered the distance "moved" by the refraction at the beginning of the sunset.
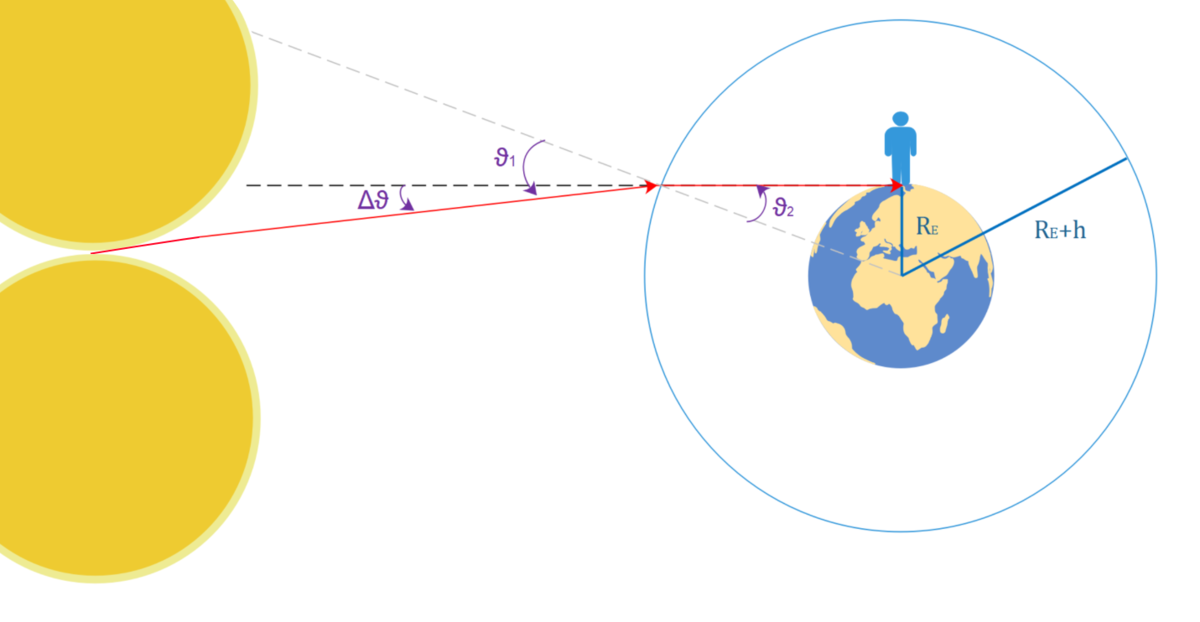
Looking at this picture, we see that the refraction effect at the start of the sunset cancels out with the effect we get at the end of the sunset. I didn't considered that in my argumentation.
My conclusion: I am not sure, if the refraction has a big influence in the duration of the sunset and using this simple model, we are not able to conclude. However, with this model we can estimate the distance d of the sun under the horizon at the end of the sunset.
I hope, this explanation answers your question!
Hey where are you? It's been a while?
You haven't replied to my question
Nice we want more
E : Earth S : Sun and D E S is the distance from the sun to earth
First of all, we know that the radiated power by the Earth and Sun is given by the Stefan-Boltzmann's law :
P E = σ A E T E 4 = σ 4 π R E 2 T E 4
P S = σ A S T S 4 = σ 4 π R S 2 T S 4
The radiation emitted by our planet comes from the absorbed radiation of the sun. The sun radiates radially heat radiation in all directions. If we imagine a sphere with radius D E S , then the ratio of the power absorbed by the earth to the power emitted by the sun is the equal to the ratio of the surface of earth cutting the sphere to the total surface of the sphere:
P S P E = A S p h e r e A E a r t h o n t h e s p h e r e = 4 π D E S 2 π R E 2 = 4 D E S 2 R E 2
⇔ σ 4 π R S 2 T S 4 σ 4 π R E 2 T E 4 = 4 D E S 2 R E 2
⇔ ( T S T E ) 4 = 4 1 ( D E S R S ) 2
Now the only unknown is the the ratio between the sun's radius and the earth-sun's distance. We can use now the information about the sunset.
To simplify the problem, let's observe the sun from the earth. Doing so, the sun orbits the earth with an angular velocity ω = τ 2 π , where τ = 2 4 × 6 0 × 6 0 s . During a sunset, the sun travels the distance 2 R S . So the angle θ travelled during a sunset (considering a circular orbit) is:
θ = D E S 2 R S
The angular velocity of the sun is constant so:
ω Δ t = 2 π τ Δ t = D E S 2 R S
⇔ D E S R S = π τ Δ t
Inserting this result in the equation above we get the following relation:
( T S T E ) 2 = 2 π ( τ Δ t )
⇔ T S = 2 π τ Δ t T E = 5 7 7 8 K