The time before they met

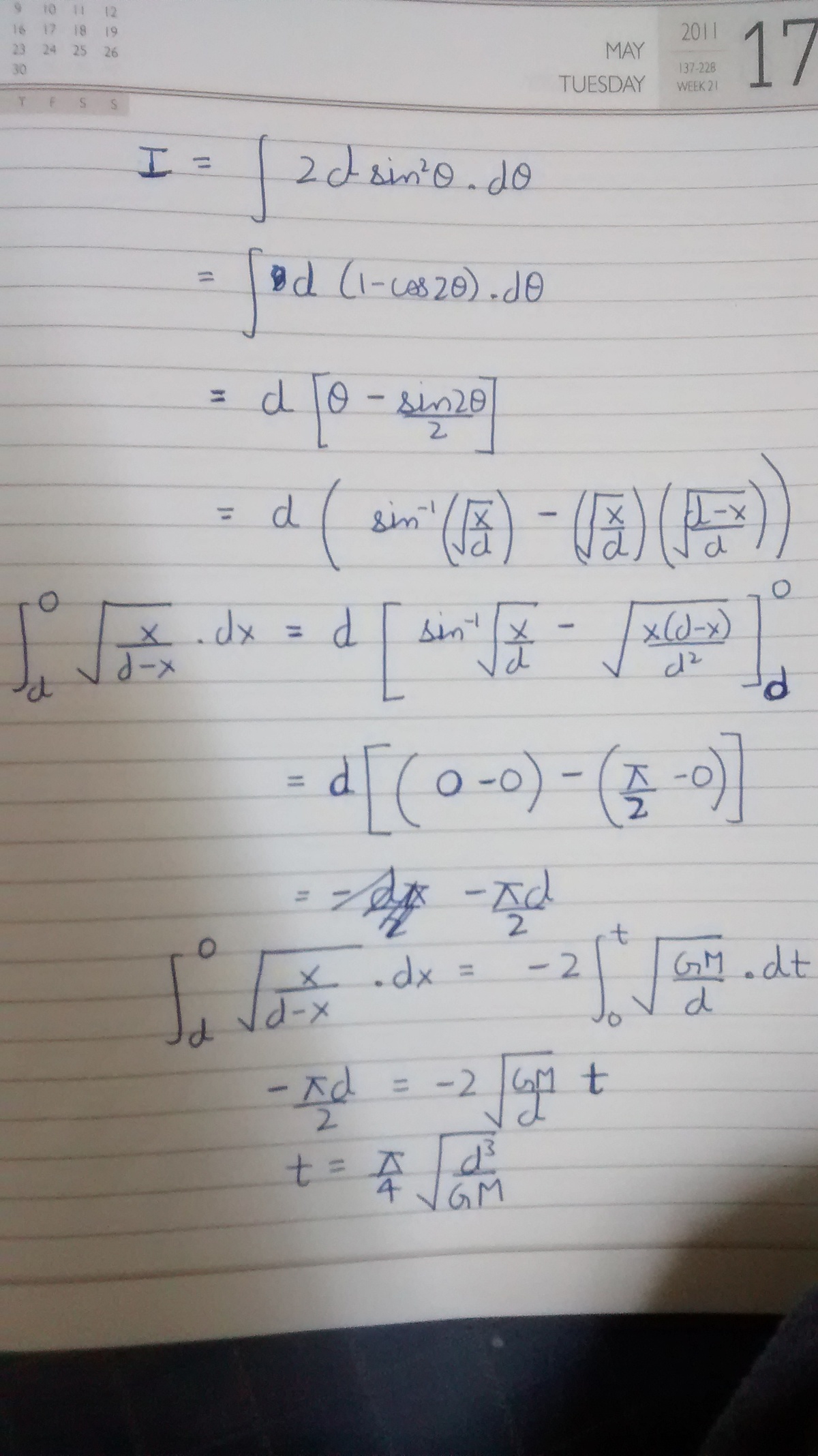
Firstly, There are two ways to start. You could either start with forming the differential equation involving acceleration and Force , Second way is by writing equation for conservation of energy. We obtain $-\dfrac{GM.M}{d^{2}}=Mv^2-\dfrac{GM.M}{x^2}$ where x is the separation between the masses. Now rearranging the terms and we obtain the expression for v. We obtain $v= \sqrt{MG\dfrac{d-x}{dx}}$ Now, $2v=\frac{dx}{dt}$ as both the bodies are approaching each other with velocity v so RELATIVE VELOCITY becomes 2v. Hence $\sqrt{\frac{dx}{d-x}}dx=\sqrt{MG}$

Integrating both sides $\displaystyle\int_{d}^{0}\sqrt{\frac{dx}{d-x}}dx=2\displaystyle\int_{0}^{t}\sqrt{MG}dt$ Now for simplicity put d=1. The definite integral can be calculated using trigonometric substitution. $2\displaystyle\int_{1}^{0}\sqrt{\frac{x}{1-x}}=\pi$

Finally , $T=\dfrac{\pi}{4}\sqrt{\dfrac{1}{MG}}$

Note---We had substituted d as 1m. Also the integral can easily be calculated by substituting $x=d\sin^2t$

A very simple technique to do this problem is using the pragmatic technique of degenerate ellipse. In mathematics, the eccentricity is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular. $e=c/a$ Being c is half of the focal length and a is half of the major axis of the ellipse. When the distance between the focus is zero $e=0$ (it’s a circle). When the distance between the focus is large, the figure becomes a straight ie $e=1$ So, we can apply Kepler's third law: $\frac{T^{2}}{R^{3}}=\frac{4\pi^{2}}{Gm}$ In this case we have e=1, c=a, m=2M because both masses are rotating virtually about their common centre. $R=a=d/2$ $T^{2}=\frac{d^{3}}{8}\frac{4\pi^{2}}{G(2M)}$ time for them to meet is $T/2=\frac{\pi}{4}\sqrt{\frac{d^{3}}{GM}}$