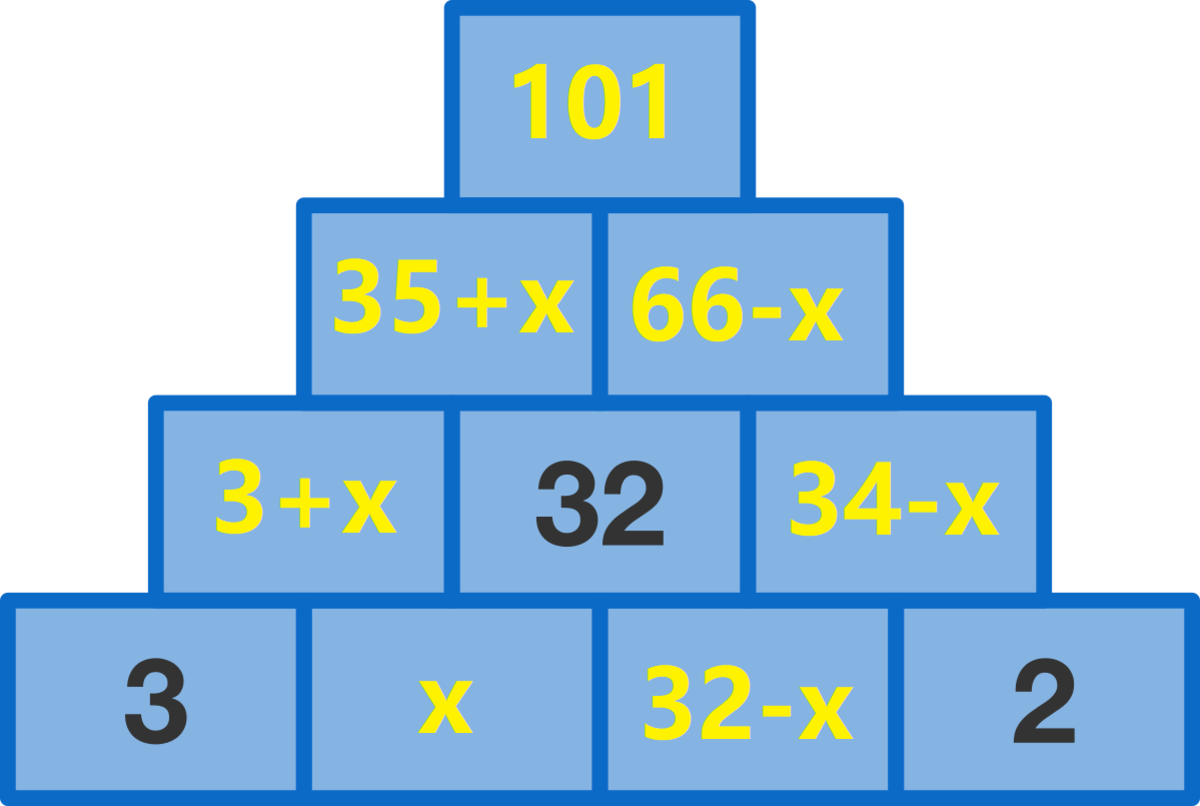
The Top Brick
The number on each brick is the sum of the numbers on the two bricks below it.
What number is on the top brick?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
18 solutions
Slightly neater algebra is obtained if you call the bottom two blocks x and 3 2 − x as in my solution
Log in to reply
Good idea. I was going for simplicity of thought rather than algebra.
Actually, Marta's is pretty simple if you skip directly from the bottom row to the top brick as a binomial expansion type of thing. This is basically a piece of a Pascal-like triangle upside-down.
Log in to reply
If you check my problems, there is another one there right after this one which is based on that general principle.
mmm why not just sum all bottom to 37 place it inside your 3+a block as 37, b+2 make as zero then place 3+a and a+b block inside 3+2a+b block as 69 and inside a+2b+2 block place a+b as 32 this way it makes everything so simple that it becomes almost funny to even call it a riddle. but don't mind me as it's my first time in here and I never do stuff like this maybe I am missing something? Just a cheeky kid :D
So why does the quiz mark 101 as incorrect?
Log in to reply
It does not.....
Please participate in my Question Game here
Love the way you explain this problem
Call the two bottom numbers x and 3 2 − x . Then perform the correct additions and the x s will cancel out, leaving the answer as 1 0 1 , as shown below
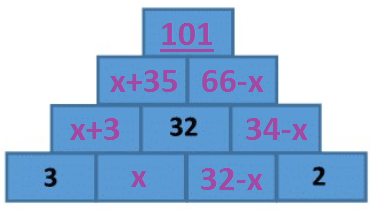
Excellent visual representation of the way I solved it (I did it in my head, mentally filling in values until I had an answer).
I did trial and error but this is a much more efficient way to get it
Please participate in my Question Game here
Fourth row: The two blanks add up to 3 2 .
Third row: The blanks left and right add up to 5 + 3 2 = 3 7 .
Second row: The blanks from the third row contribute 37, and the middle value of 32 contributes twice. This makes the total 3 7 + 2 × 3 2 = 1 0 1 .
First row: The top block is the total of the second row, i.e. 1 0 1 .
"blanks from third row contribute 37" *
Log in to reply
Luke -- Forgive me for asking this -- What does your post mean ? What is the meaning of the asterisk ?
Log in to reply
Luke posted a correction on my solution. Originally I wrote "32" instead of "37", and Luke notified me of that error. It has been fixed now.
Log in to reply
@Arjen Vreugdenhil – Okay. Thanks for the reply/info.
If there is a unique solution (and there must be), then it doesn't matter what numbers you put in the bottom row so long as they add to 32. In fact picking any two numbers and quickly adding up the pyramid may be faster than developing and solving the problem using the general algebraic approach shown in other solutions.
"IF there is a unique solution." That's the key. A solution to be valid should not only choose the correct option, it should show that there is a solution.
Please participate in my Question Game here
No matter what number you assign for the bottom 2 bricks, the final sum on for the block at the top is constant. This is because if you add +1 to one brick, you'll then have to subtract -1 away from the other one and therefore the overall effect is 0. So, we can just pick 2 random numbers and assign them for the 2 bricks and work it out all the way to the top as long as the 2 numbers add up to 32.
That's like "put one foot in front of the other" as a direction to a place. True, but not sufficient to let people know just what to do.
3 + 2 + 32 * 3 = 101.
The 3 and 2 are on the edge so they are carried up to the top as they are.
The 32 is used 3 times, once it is split and part of it makes up each brick to the left and right of it. It is then duplicated twice for the two bricks above it.
For these kinds of puzzles they can be solved by working out how many times the value for each brick is used, of course it's much harder to work out on larger puzzles.
You have given numbers of 32, 3, 2. Start by dividing 32 to get numbers that fill the entire bottom row. From there you add to get each sum.
32/2 = 16.
16+3=19. 16+2=18.
19+32=51. 18+32=50.
50 + 51 = 101
 The top brick is
3
+
3
(
a
+
b
)
+
2
=
3
+
3
×
3
2
+
2
=
3
×
3
3
+
2
=
9
9
+
2
=
1
0
1
The top brick is
3
+
3
(
a
+
b
)
+
2
=
3
+
3
×
3
2
+
2
=
3
×
3
3
+
2
=
9
9
+
2
=
1
0
1
This is actually a very simple puzzle, since you can insert any two numbers (a and b for example) to the bottom row, as long as a + b = 32.
This is true, but you don't show why you can put in any numbers.
Bottom row: 3, 32-x, x, 2 Second row: 35-x, 32, x+2 Third row: 67-x, 34+x Top row: 101
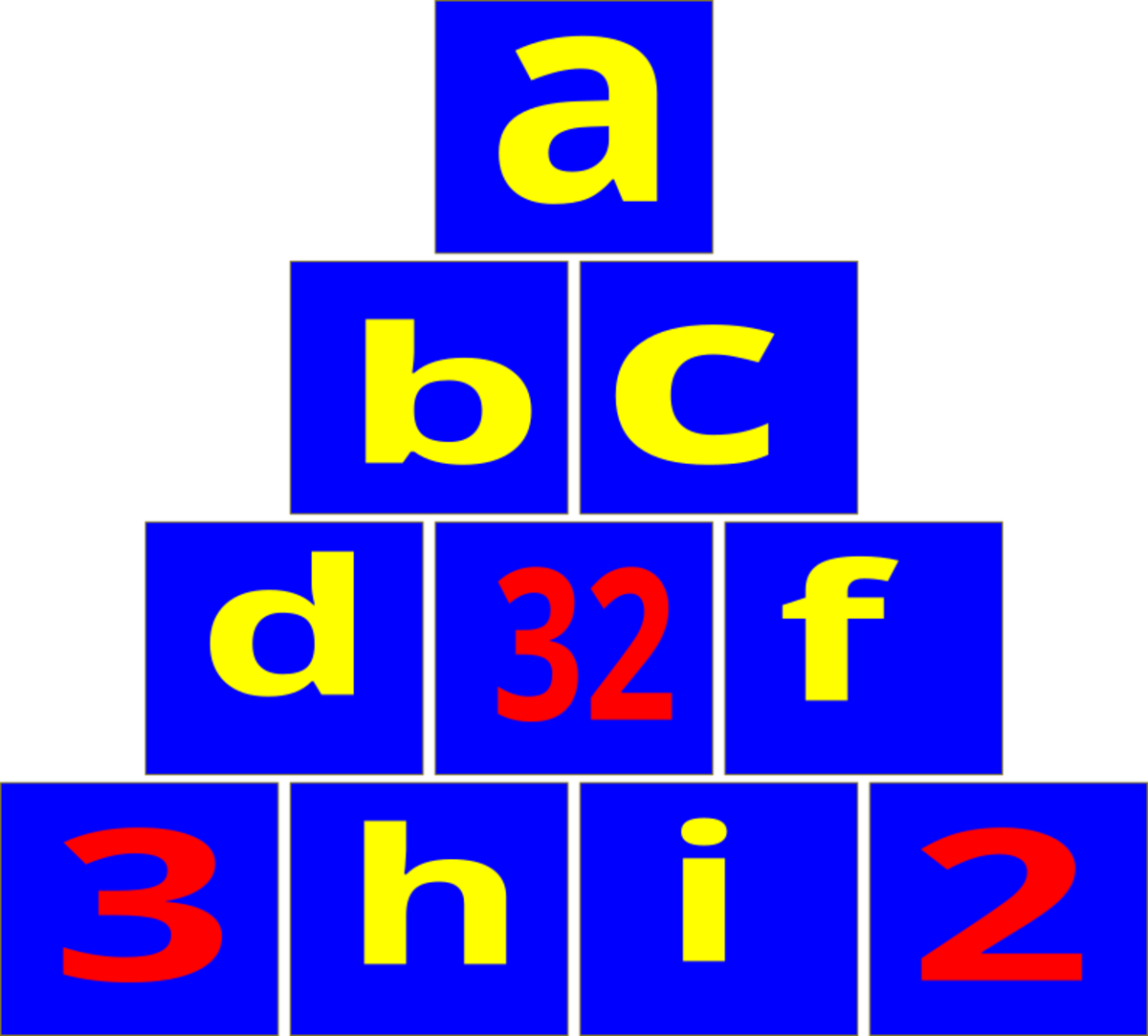
a = b + c
b = d + 3 2 , c = 3 2 + f
d = 3 + h , 3 2 = h + i , f = i + 2
a = 3 + h + 3 2 + 3 2 + i + 2 ⇒ ( 3 ∗ 3 2 ) + 5 = 1 0 1
Nice, but already posted by another person.
In the bottom line suppose the numbers are =a,b Here we get, a+b=32 So the number on the to would be =3+a+32+2+b+32 =a+b+69 =32+69 =101
Let the blanks in the bottom row be l and r for left and right, respectively.
The square to the bottom-left of the top is the sum of the ones below itself, namely ( 3 + l ) and 32, and the square below the top to the right is the sum of 32 and ( r + 2 ) . Add and simplify to find that the top square = l + r + 6 9 .
The square marked 3 2 is the sum of the two below it, so l + r = 3 2 .
We now have two equations. Let me add parentheses to give a hint: t o p = ( l + r ) + 6 9 ( l + r ) = 3 2
Substitute the quantity ( l + r ) into the first equation from the second: t o p = ( l + r ) + 6 9 = 3 2 + 6 9 = 1 0 1 .
I just kept splitting 32 in different ways until I found a way that worked.
Any split will work. That's the idea of it. And a solution should show that this is so.
Just in case somebody would like to feel it instead of solving it in algebraically, they should keep in mind that the first and foremost part of breaking the number 32 into two components would not depend on how you break it. It is because all numbers are being added in every successive step, so there is no loss of any existing unit in the process, and the answer comes out the same no matter how you break 32.
Pick any 2 numbers that add up to 32 and place them in either box below 32 and simply solve up .
That works for getting a choice between the numbers. But it assumes that the problem is well defined, in a sense that it does have a solution. It does not prove that the solution actually exists.
Log in to reply
I solved for the row below using whole numbers. 2 1 15 1 1 was the only whole number choice that seemed to fit.
Log in to reply
First of all, there is no row below. Second, if there were one, it could be 1 2 15 1 1 or 1 1 14 1 1 as well.
I figured that in order for this to have a solution, it wouldn't matter what the two missing numbers were as long as they added to 32. So tried 32 and 0 and then tried 16 and 16 and low and behold, 101...
That works fine for getting an answer based on the assumption that the problem does have a solution. It does not solve it in a general way, however. If there was an option of "it depends," you could not be so sure. Of course, the Brilliant staff makes sure the problems they select are okay.
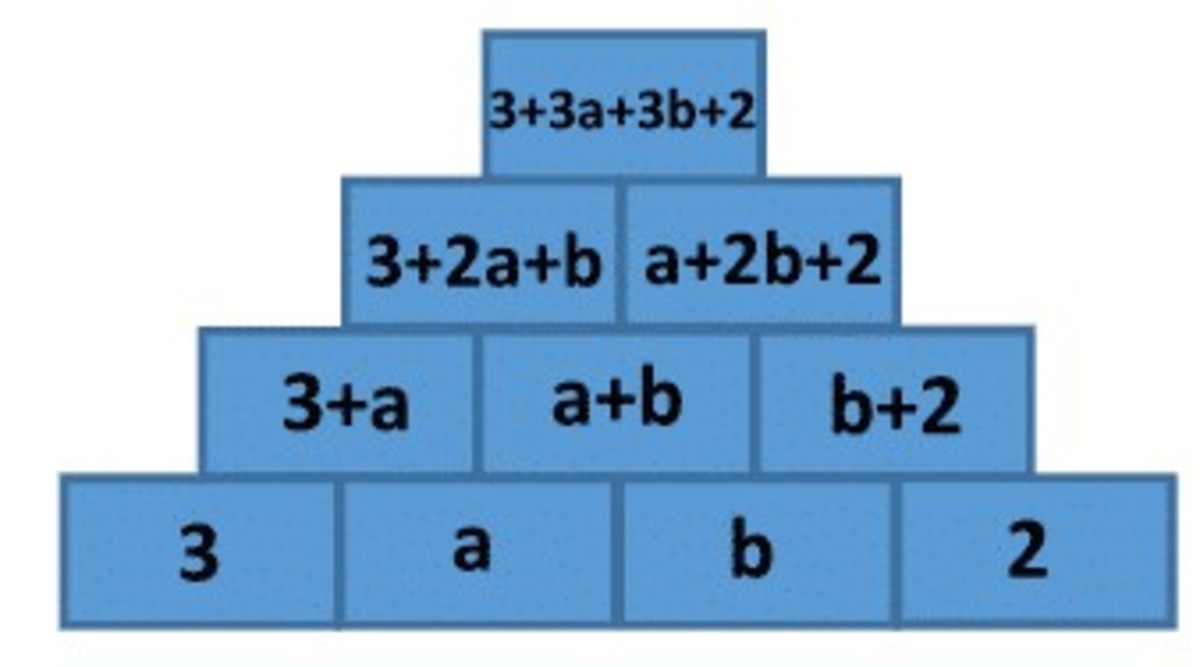
The top brick is 3 + 3 a + 3 b + 2 = 3 ( a + b ) + 5 .
But we know that the center brick in second row from the bottom is a + b = 3 2 .
So the answer is 3 ⋅ 3 2 + 5 = 1 0 1 .