The two moons
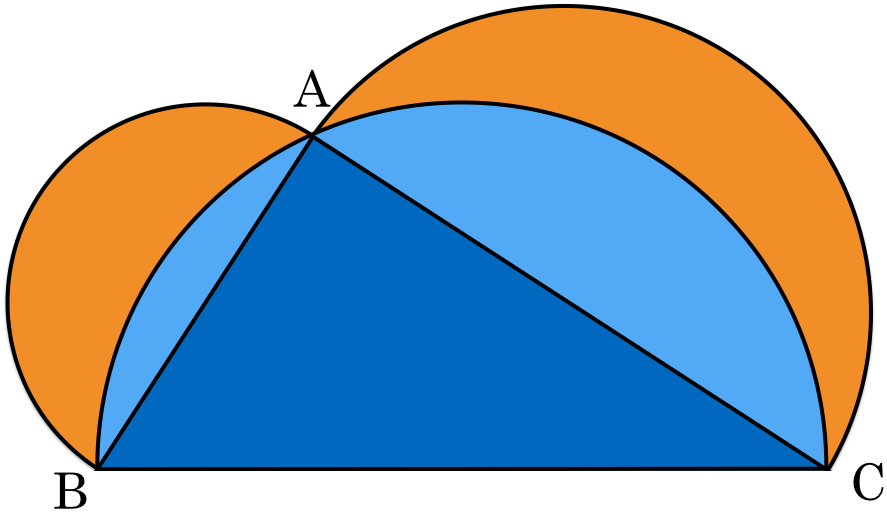 Consider a triangle
A
B
C
with right angle
A
,
B
C
=
5
and
A
C
=
4
.
Three semicircles are drawn as in the figure above. Find the sum of the areas of the orange shaded regions.
Consider a triangle
A
B
C
with right angle
A
,
B
C
=
5
and
A
C
=
4
.
Three semicircles are drawn as in the figure above. Find the sum of the areas of the orange shaded regions.
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Pythagoras’ Theorem says that if the three sides of a right angle triangle subtend similar figures, then the area of the largest equals the sum of the areas of the two smaller. Here the figures are semicircles. So area of (dark blue + light blue) = area of (orange + light blue). Thus area of orange = area of dark blue = 3x4/2 = 6.
You won't believe I did not see the values of the segments AC, BC; I started algebraic:
- Assume x = AB, y = AC and z = BC.
- Orange will be half circle area of radious x/2 + half circle area of radious y/2 minus difference of half circle area of radious z/2 and triangle area.
Hence:
[ π * (x/2) ² ] / 2 + [ π * (y/2) ² ] / 2 - { [ π * (z/2) ² ] / 2 - xy/2 }
Factorizing:
π / 2 * [ (x/2) ² + (y/2) ² - (z/2) ² ] + xy/2 = π / 2 * [ x²/4 + y²/4 - z²/4 ] + xy/2 = π / 2 * [ ( x² + y² - z² ) / 4 ] + xy/2 =
replacing "z" by its value in terms of X and Y: z = sq[ x² + y² ] , hence z² = x² + y² ; we get:
π / 2 * { [ x² + y² - ( x² + y² ) ] / 4 } + xy/2 = π / 2 * ( 0 / 4 ) + xy/2 = π / 2 * 0 + xy/2 = xy/2
And because the blue triangle's area happens to be xy/2; hence, *no matter what the segments measure is, the Orange area is always the same one than the blue triangle.
Nice! Thank you!
Thanks. I was shocked when I found the answer had no irrational portion left to it. I was going to brute force it out, but I see you already did.
Beautiful Application of Algebra! But can we find the individual areas of the two hemispheres? TIA.
Orange region is = Two small semicircles - (large semicircle - Triangle area) = Triangle area = 6.
I think you need to show why the two small semicircles = the large semicircle. It's not apparent. In fact, between A and B, the blue almond is much smaller than the orange moon. Conversely, between A and C, the blue almond appears to be bigger than the orange moon.
Log in to reply
it's similar to Pytagora's Theorem: in this case we have semicircles instead of squares:
http://oi67.tinypic.com/2cr0rpv.jpg
thats the famous blob-pythagorean theorem, which btw quite elegantly proves itself and thereby the regular one. https://www.youtube.com/watch?v=ItiFO5y36kw
Pythagoras’ Theorem says that if the three sides of a right angle triangle subtend similar figures, then the area of the largest equals the sum of the areas of the two smaller. Here the figures are semicircles. So area of (dark blue + light blue) = area of (orange + light blue). Thus area of orange = area of dark blue = 3x4/2 = 6.
 Image
Image
Log in to reply
 Image
Image
Log in to reply
FYI You have to link to the actual image, and not the url of the entire page. I've edited your comment.
Log in to reply
@Calvin Lin – Ok! thank you
Log in to reply
@A Former Brilliant Member – In future, please post it as your own solution, instead of as a comment. Thanks.
By Pythagoras AB=√5²-4²=3 cm
Sum of the orange is (area) ABsemicrc+ACsemicrc-(BCsemicrc-ABCtri)
ABsemicrc=½π(AB/2)²=9/8π cm²
(half the area of a circle is ½(πr²))
ACsemicrc=½π(AC/2)²=2π cm²
BCsemicrc=½π(BC/2)²=25/8π cm²
Area of ABCtri=½(3)(4)=6 cm²
We notice that ABsemicrc+ACsemicrc=BCsemicrc=25/8π cm²
So area of orange equals area of triangle Or by substitution in the equaution of the sum
Orange area = ABsemicrc+ACsemicrc-(BCsemicrc-ABCtri) =9/8π+2π-(25/8π-6)=6 cm²
Therefore area of orange area equals 6cm².
I like the way solve this question
The sum of the two orange regions = the sum of two orange semi-circles - [area of blue semi-circle - area of the triangle] =(1/2) pi (3/2)^2 + (1/2) pi (4/2)^2 - [(1/2) pi(5/2)^2 - (1/2) (3) (4)] =(pi/8) (9+16-25) +6 =6.Ed Gray
The Theorem of Hippocrates (ca. 430 B.C.) infers that the sum of the areas of such 'lunes' equals the area of the base triangle; along with Pythagoras' Theorem one arrives at 6 units squared.

Note that when a triangle is inscribed in a circle or semi-circle such that one of its side is the diameter of the circle or semi-circle, it is a right triangle. Since the hypotenuse is 5 and one of the legs is 4 , the other leg must be 3 (use pythagorean theorem). The area of the orange region is equal to the area of the inscribed triangle. We have, 2 1 ( 3 ) ( 4 ) = 6
Here is the proof.
Consider my diagram. Let x and y be the legs and z be the hypotenuse of the right triangle. The area of the orange region is equal to the area of the semi-circle with diameter x plus the area of the semi-circle of diameter y plus the area of the right triangle minus the area of the semi-circle with radius z . We have
A = 4 π x 2 + 4 π y 2 + 2 1 x y − 4 π z 2 = 4 π ( x 2 + y 2 − z 2 ) + 2 1 x y
But, by pythagorean theorem, we have, z 2 = x 2 + y 2
So, we have
A = 4 π ( z 2 − z 2 ) + 2 1 x y = 2 1 x y
Hence, proved.