The unending streak of circles and sticks
A large number of sticks (with mass density
ρ
per unit length) and circles
(with radius
R
) lean on each other, as shown in the figure below.
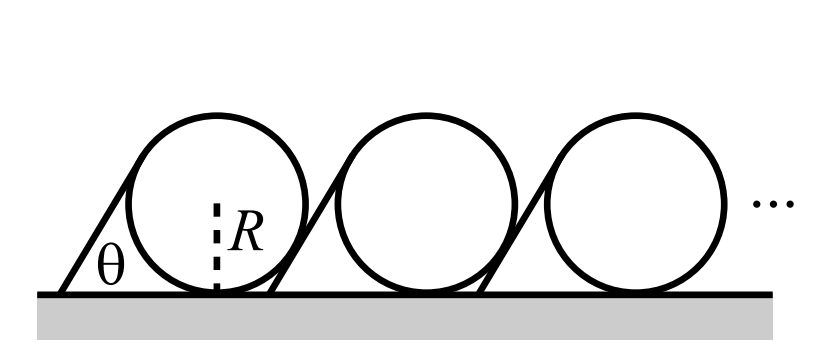
Each stick makes an angle θ with the horizontal and is tangent to a circle at its upper end. The sticks are hinged to the ground, and every other surface is friction less.
In the limit of a very large number of sticks and circles, what is the normal force between a stick and the circle it rests on, very far to the right? If you find result as S give the as [ S ] , where [.] represents the ceiling function.
Details and assumptions:
- The last circle, i.e. the circle at infinity is leaning against a wall (which has only the significance of stopping the whole system from moving)
- Take ρ = 1 , R = 1 5 , g = 1 0 m/s 2 , θ = 7 4 ∘ .
- Every value is given is S.I. system.
Hint: As always, generalize the result for any N and then take the limit as N tends to infinity .
The answer is 64.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
 please zoom in if you find it small, thanks !
please zoom in if you find it small, thanks !
I don't know much about the physics of this, but I do have concerns about "Prove the result for finite N with a wall, and then assume that the infinite case is the limit of the finite case". There are several claims which are not true in the infinite case by taking the limit.
Log in to reply
no sir, the question is exactly fine and it is the only thing needed for solving it as far as wall is concerned , i wrote in the question that it has only work of stopping the circles from moving and nothing else ! :) and the statement of taking limit was a hint as this is how we proceed in questions like this , we find for any "n" and then , if the limit converges,we find it , if it diverges , such physical position can't exist ! but in this case, since limit exists , this situation is obviously fine :) if you still do not believe me , we may hear sir @Josh Silverman
Log in to reply
I don't have a problem with the approach. At some point, a circle at the near end shouldn't be able to feel a difference from the far (large N ) end.
I would though highly discourage screenshot solutions.
@Harsh Shrivastava you were demanding a problem , here it is ! have fun bro :)
Log in to reply
Had fun! Nice problem.
I am happy that I solved it.
Now my turn to post a problem!
Will post a problem soon(buzy this week due to inmo)
From which book is this problem?
Log in to reply
Its from David Morin!!!
Log in to reply
@A Former Brilliant Member – Oh I see.thanks.
Log in to reply
@Harsh Shrivastava – Do you use this book?
Log in to reply
@A Former Brilliant Member – No.But I have a PDF of it.
Log in to reply
@Harsh Shrivastava – Its a nice book,but the main problem is answers to exercise questions are not avalaible.
Log in to reply
@A Former Brilliant Member – do you hve doubt in ny excercise uestion, i my be of some help :)
Log in to reply
@A Former Brilliant Member – Do you have answers of all questions?
@A Former Brilliant Member – The problem is I don't have doubts but I just want to verify answers.
Actually can you please help me,I have been solving the book by David morin,but the problems is where do I get the answers to the exercise questions?
Very nice problem and well written solution !
A minor suggestion: when numerically evaluating N ∞ , i find 63,48.
Do you agree ?
If so, could you specify in the problem that the result must be rounded up to the nearest integer ? Thank you
Log in to reply
oh , yes . i will write to give result as in ceiling function , i took theta as 4/5 .
You do not need to do the infinite series. Simply assume that N i = N i + 1 = N and solve for N . The torque equation for the rod is
N ℓ − N ′ ℓ ′ − m g 2 ℓ cos θ = 0
Here ℓ = R cot θ / 2 , ℓ ′ = R tan θ / 2 and m = ρ ℓ . From the balance of forces for the ring we get:
N = N ′
Solving for N yields:
N = 2 ρ R G cot θ / 2 − tan θ / 2 cos θ / tan 2 θ / 2 = 2 ρ R G sin θ / 2 cos 3 θ / 2 = 6 3 . 4 8 N