The Year in a Diagonal.
The numbers in the circles follow the pattern shown below.
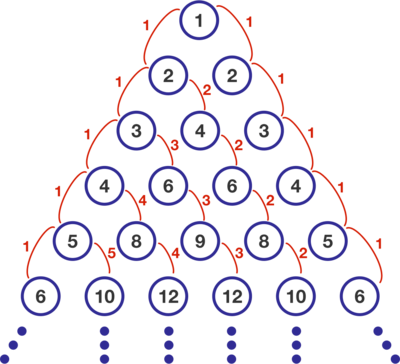
In which horizontal row of circles does the number 2 0 1 8 first appear?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
16 solutions
Thank you, nice solution.
2+3-1 = 4 ;-)
Brilliant really. Thanks
I simply observed the table, noted that 12 appeared for the first time in the sixth row, and that the biggest figures in the earlier rows were less than double the row number and decided on that basis that answer would the option closest to 2018/2, fortified in this opinion by the fact this is a basic level question.
Log in to reply
You got lucky. When does 2017 show up?
Log in to reply
Hehe... Though i would've gone in the other direction and asked "When does 2187 show up?" ;-) (or 2048)
since 2017 is prime it cant present itself in any of the tables that are embedded, so no chance until the 2017th row
The n th contains precisely all numbers of the form x ⋅ y where x + y = n + 1 . For instance, the 6th row contains 1 ⋅ 6 = 6 , 2 ⋅ 5 = 1 0 , 3 ⋅ 4 = 1 2 , 4 ⋅ 3 = 1 2 , 5 ⋅ 2 = 1 0 , 6 ⋅ 1 = 6 . To answer the question for a number A , we must therefore find two factors x ⋅ y = A with x + y = n + 1 minimal. This minimum is obtained when x , y are as close to each other as possible, and as close as possible to A ; if we list the factors of A from smallest to greatest, they will be the two factors in the middle of the list, or the one factor A in the middle if A is a perfect square.
The factors of A = 2 0 1 8 are: 1 , 2 , 1 0 0 9 , 2 0 1 8 Thus n + 1 = 2 + 1 0 0 9 = 1 0 1 1 and the answer is n = 1 0 1 0 .
Proof : If x ⋅ y = A , let f ( x ) : = x + y = x + A / x . Moreover, if we assume x ≤ y then 1 ≤ x ≤ A . The derivative is f ′ ( x ) = 1 − x 2 A ≤ 0 on the given domain, showing that f is a decreasing function there. Thus the closer we choose x to A , the smaller n = f ( x ) will be.
Arjen -- Is there a name for that kind of triangle (like another triangle is Pascal's triangle) ?
Log in to reply
It is a multiplication table, turned 45 degrees!
Log in to reply
And now I see that, having gained the benefit of your reply. Thanks much. As always, I am fascinated by your posted solution. Did you see the problem about weighing astronauts in space ? Pretty nifty apparatus, that thing.
Log in to reply
@Jesse Otis – Yes, the astronaut on the spring will vibrate with a frequency equal to f = 2 π 1 m + 3 1 m 0 k , where k is the spring constant and m 0 the mass of the spring (assuming that the spring's mass is homogeneously distributed along its length).
Log in to reply
@Arjen Vreugdenhil – Nice. I don't think that I have ever seen that particular 'rendition' of the f equation (with (1/3) m0 in the denominator under the radical).
The general expression for each row, where r is the row number and n is the term, is
n ( r − n + 1 )
Solving for r where this is equal to 2 0 1 8 , we get
r = n 2 0 1 8 − n + n 2
so that the mininum positive integer r is 1 0 1 0 .
Thank you, nice solution.
How would you get from r = n + 2018/n - 1 to "minimum of 1010"? -.-
Log in to reply
You can differentiate perhaps?
Log in to reply
Good point. Though that applies to continuous functions, so there would need to be a bit more checks and steps...
Still, imo, that's an important part of the solution that is missing from Michael's explanation.
How do you get the "general expression"?
Log in to reply
Look at how the triangle was constructed: each of the series going down and to the right is k n , and it starts on the k-th row. So on the r-th row, we have (going right-to-left): 1 ∗ r , 2 ∗ ( r − 1 ) , 3 ∗ ( r − 2 ) , ..., ( r − 1 ) ∗ 2 , and r ∗ 1 . Now numbering the values with n=1,...,r , we get n ∗ ( r − n + 1 ) . Also, it can be noticed that the values on each row are symmetrical, so numbering left-to-right will actually give the equivalent formula ( r − n + 1 ) ∗ n .
Each number is the product of the numbers at the tops of either diagonal that pass through it. For example on the above, 8 = 2 × 4 and 8 = 4 × 2 .
This means we can work out the row of a number by adding one of its cofactor pairs, then subtracting 1 (as both diagonals share the starting 1). Using the same example, 8 appears on the line 2 + 4 − 1 = 5 .
The factors of 2 0 1 8 are 1 , 2 , 1 0 0 9 & 2 0 1 8 . This means the number 2 0 1 8 will appear on rows 2 + 1 0 0 9 − 1 = 1 0 1 0 and 1 + 2 0 1 8 − 1 = 2 0 1 8 , the lower of which is 1 0 1 0 .
If we watch the numbers from left to right the first numbers is always the rows number(rn), the second number(x) is twice then the previous row number. Inversely: rn=(x/2)+1 now x=2018.
rn=(2018/2)+1=1009+1=1010
Did the same.
Taking the only one of two factors of 2018...1009.
2018 will now be just below 1009th row... i.e 1010th row
The expression "LCM of 2018" is quite meaningless... :-|
Also, how exactly is 1009 a multiple of 2018?!
We can simple divide 2018 by 2 and get 1009 and round it of to 1100 as this is a Pascal's triangle and two is the smallest factor of 2018 other than 1.
I just figured out that the first one it would show up in would be the one that would be around half of the end number as X 2 will be the earliest it can be seen other than in it's own row. Then by looking at the pattern I saw that the second number in each row was double the first number minus 2. From there, look at the options and 1010 X 2 = 2020 - 2 =2018. It will be the second number in the 1010th row.
Note that the second entry on each row is given by 2n -2 and are all multiples of 2. So if 2n - 2 = 2018, 2n = 2020, and n = 1010. Ed Gray
Deducing a formula by extending the series 7 12 15 16 15 12 7 8 14 18 20 20 18 14 8
R2 = x + (x-2) ; where R2 is the second element in the row from left and x is the row number. R2 = 2018; x = ?
Solving the equation 2x=2020; Thus x=1010
After I looked at this triangle I observed a simple pattern which only even numbers followed.
To find the row in which they first appeared just divide the number by 2 and add 1 to the answer.
For example :-
4 , 4/2 +1 row , 3rd row.
6 , 6/2 +1 row. , 4th row.
.....
2018, 2018/2 +1 row, 1010th row
First of all, the number 2018 cannot appear in the row whose value is the quotient of 2018 and 1,3,4 or 5. This is is shown by the answer choices. By this I mean 2018 divided by 1 is 2018 and so this number cannot be as it’s not in the list, and 2018 divided by 3, 4 or 5 does not give a whole number.
This division I’m doing may seem a little unclear. I’m dividing numbers because the each pattern is basically the 1, 2, 3, 4 or 5 times table, so dividing numbers finds how many times each number goes into 2018, and therefore the row number.
2 is the only number which goes into 2018; it goes 1009 times. But there’s no 1009th row you ask. Well the 2 times table doesn’t appear until the 2nd row, so you add one to 1009, giving the 1010th row.
Notice that each of the two sides increase by one, thus 2018 must appear on the 2018th row on either sides, but can it appear sooner? Well, what about the side that increases by two? with a simple division 2018/2 you get 1009, meaning that it will appear on the 1009th row (counting from the first row that has 2). Finally, you just add the first row that contains 1, and you get 1010th row (the right answer
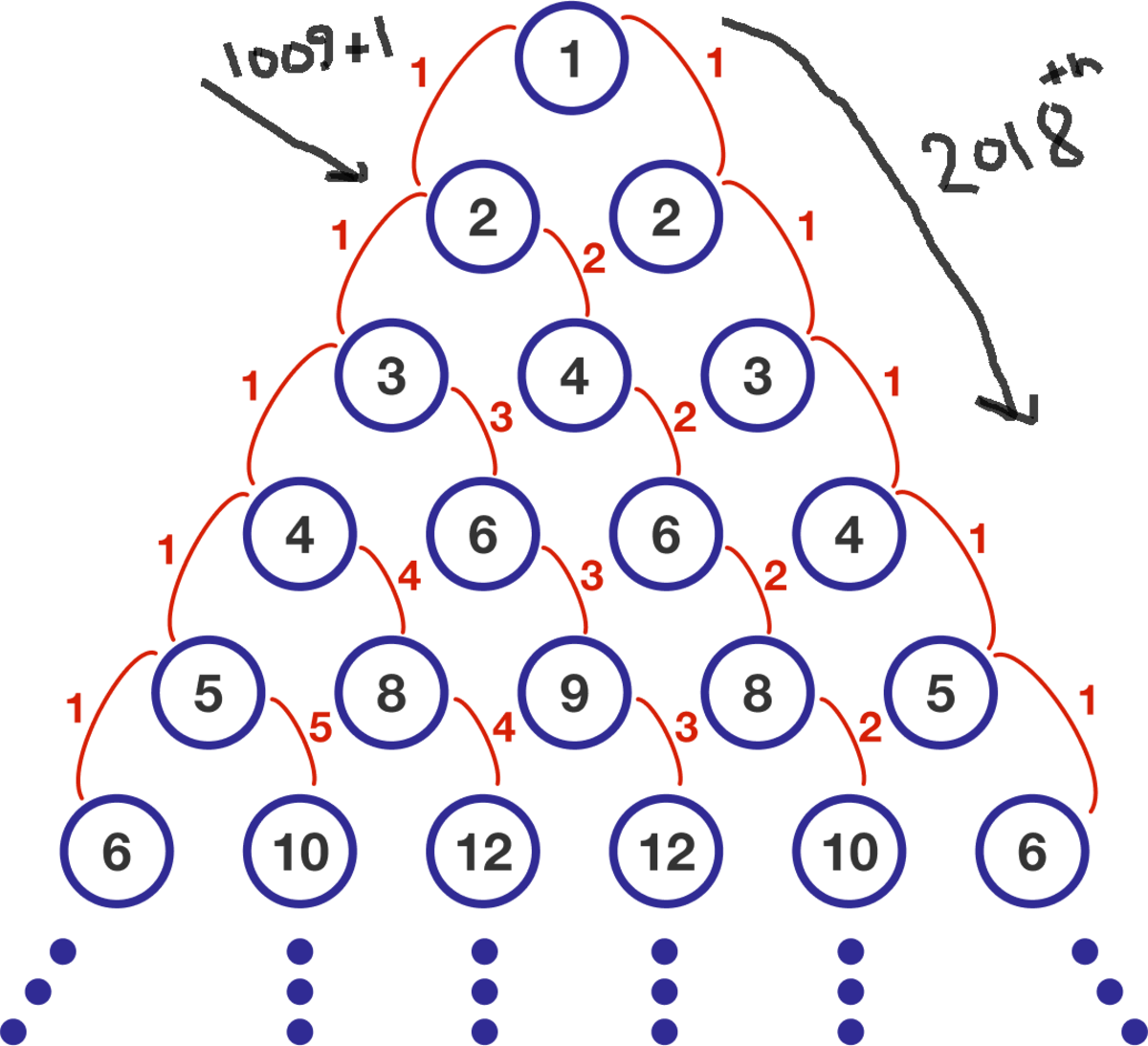 ).
).
This is what I noticed. I then stop trying to find the general formula and see if I could try each possible answer in turn. The first possible answer was 1010 row, so I thought 1010 * 1 is not that then, then I tried 1009*2 , which was it! Did our questioner take mercy on those who would go the exhaustive method? He He
Factors of 2018 are 2,1009 From symmetry, 3,5,....are prime numbers and their double i .e, (3×2)OR(5×2) appears at the the next of 3rd or 5th rows respectively. Such that ,2018 will appear to the next row of 1009 i .e, 1010 th row.
It is seen that every even no. (n) appears for the first time in the (n/2)+1 row. So, 2018 appears in the row: => (2018/2)+1 => 1009 + 1 = 1010
Each row is marked on the sides with its row number, and the sum of the two markers is always in the next row below. If 2018 is the result of two markers, that is 1009, and the row after that is the 1010th.
If a number n can be factored as x ⋅ y then n will appear in row x + y − 1 . For example the number 6 appears in row 1 + 6 − 1 = 6 but also row 2 + 3 − 1 = 4 .
2 0 1 8 has only two factorizations, so appears in rows 1 + 2 0 1 8 − 1 = 2 0 1 8 and 2 + 1 0 0 9 − 1 = 1 0 1 0