There are no side lengths!
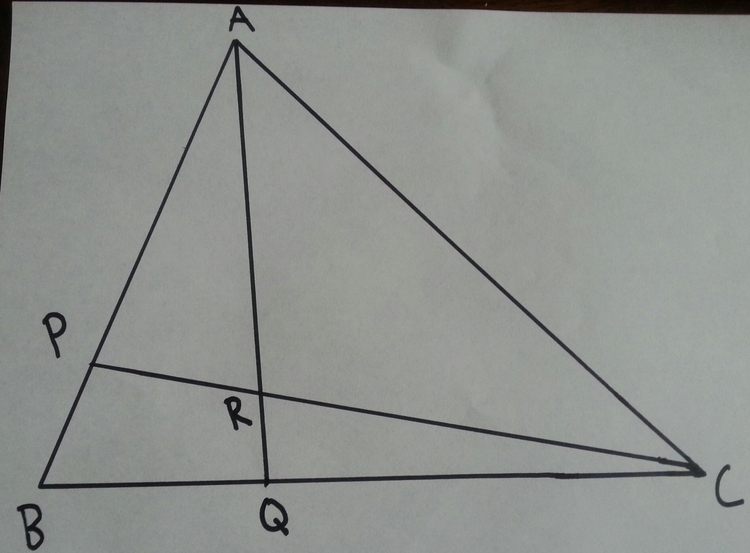Let
A
B
C
be a triangle with points
P
and
Q
respectively lying on line segments
A
B
and
B
C
, such that
P
B
A
P
=
3
and
Q
C
B
Q
=
2
1
.
If lines A Q and C P intersect at R , the ratio R Q A R can be expressed as b a where a and b are coprime integers. Find a + b .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Nice, this was my solution as well.
Did the same
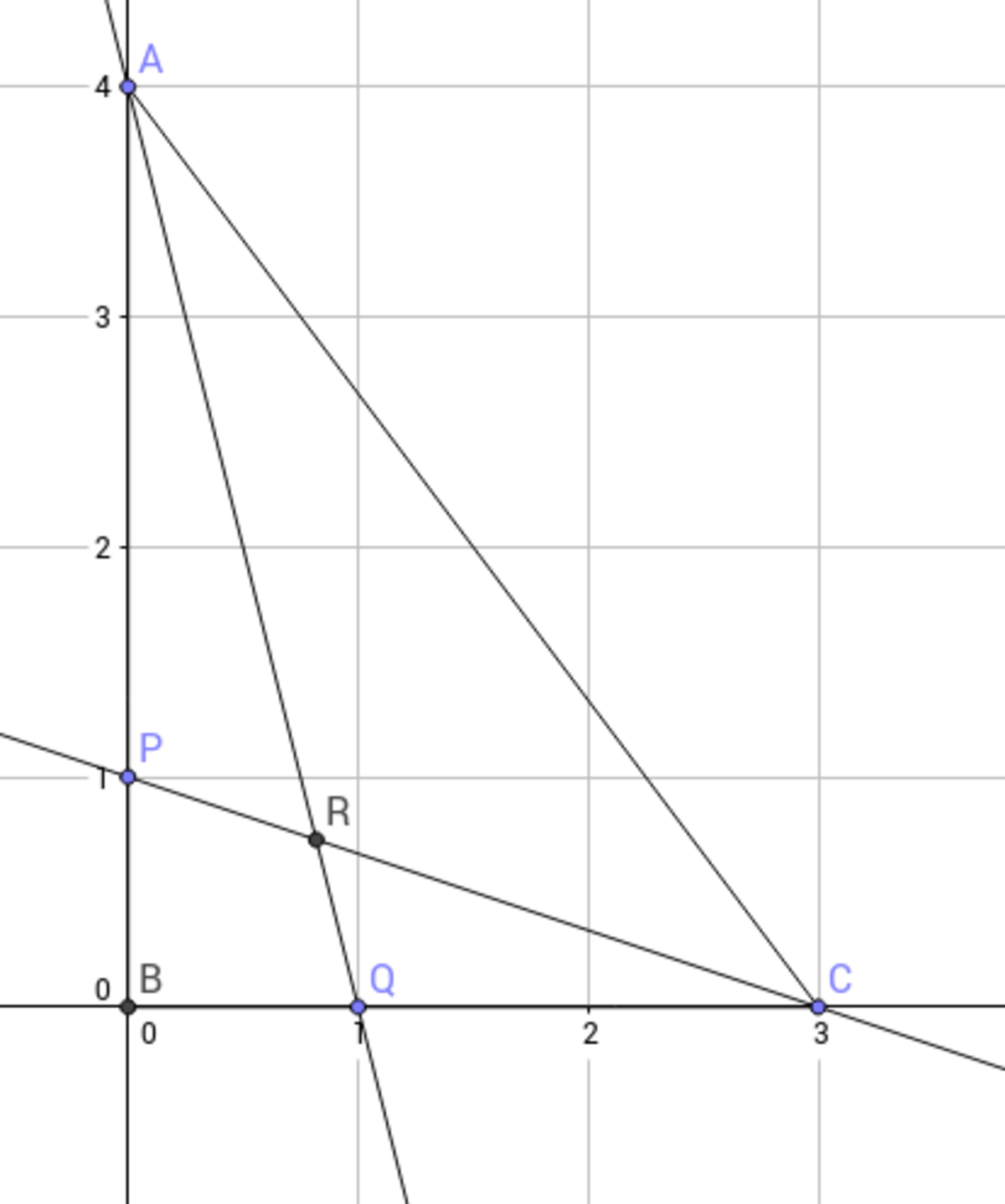Without lost of generality, we can take in a Cartesian plane, B(0;0) A(0;4) and C(3;0) so we can easily find that
R
(
1
1
9
;
1
1
8
)
and
R
Q
A
R
=
1
1
8
4
−
1
1
8
=
2
9
So a+b=11
Nice coordinate bash.
Mass Points!
Give A, B, C the weights 2, 6, 3 respectively. This means that Q has a weight of 9. Which means that R Q A R = 2 9 ⟹ 9 + 2 = 1 1
Weights? Can you explain
Log in to reply
The idea of mass points is basically by using a local coordinate system and identifying points by the ratios into which they divide line segments.
It involves systematically assigning "weights" or "masses" (they are interchangeable) to points using ratios of lengths relating vertices, which then you can use to find other lengths, using the fact that the lengths must be inversely proportional to their weight.
Imagine a lever of length 7. Denote the endpoints as A and B. If you put a mass of 4 on A and a mass of 3 on B, the balance point, C, must be three units away from A and four units away from B. Additionally, the balance point has a mass equal to the sum of the mass of both endpoints. So in this case, C would have a mass of 7.
An example of this is imagine segment XY. Let Z be on the segment such that XZ = 2 and ZY = 5. This means you can put a mass of 5 on X and a mass of 2 on Y.
Another example, a triangle with all of it's medians drawn.
Call the triangle ABC, and let D, E, F be the midpoints on BC, AC, AB, respectively. Let G be the centroid. Thus, if you label A with a mass of 1, since B and A are equidistant from F, B also has a weight of 1. And likewise, C has a weight of 1. The midpoints between ABC have weights of 2, because they are the sum of the two endpoint. Thus, we can deduce that the centroid splits the median into two parts with a ratio of 2:1 (since the weights are 2 and 1)
Using mass points with the fact that for any set of points, there is one unique center of mass, can be powerful.
Log in to reply
Then, how can you say that R is the balance point of AQ? Proof?
Log in to reply
@Kishore S. Shenoy – In any set of three points, the center of mass is unique.
Consequently, the center mass of the third point with the center of mass with the other two points is the center of mass of all three points.
Therefore, since C is connected to the center of mass of A and B, you know the center of mass must be on this segment.
Also, since A is connected to the center of mass of B and C, the center of mass lies on this segment.
Since the center of mass is unique, it must be the intersection of the segments, which is namely, R.
Really awesome method .loved it
JUST APPLY MENELAUS THEOREM FOR triangle ABQ
First we let P A = 3 x , P B = x , B Q = y , Q C = 2 y , A R = a and R Q = b . After it I drew a parallel line to B C passing through P , intersecting A Q at D . As A B Q ~ A P D we have P D = 4 3 y and A D = 4 3 ( a + b ) , but Q C R ~ D P R , so R D = 8 3 b . Therefore a − 8 3 b = 4 3 ( a + b ) = > 2 a = 9 b = > b a = 2 9 = > a + b = 1 1