There is a formula for this volume calculation
A solid polyhedron has two square parallel faces (bases) of side length 1 0 units, and the two squares have a skew angle between them of 4 5 ∘ . The other eight faces of the solid are planes passing through a side of one of the two bases and the opposite vertex of the other base. The vertical height of the solid (the vertical separation between the two bases) is 2 0 units. This is shown in the image below. Find the volume of this solid.
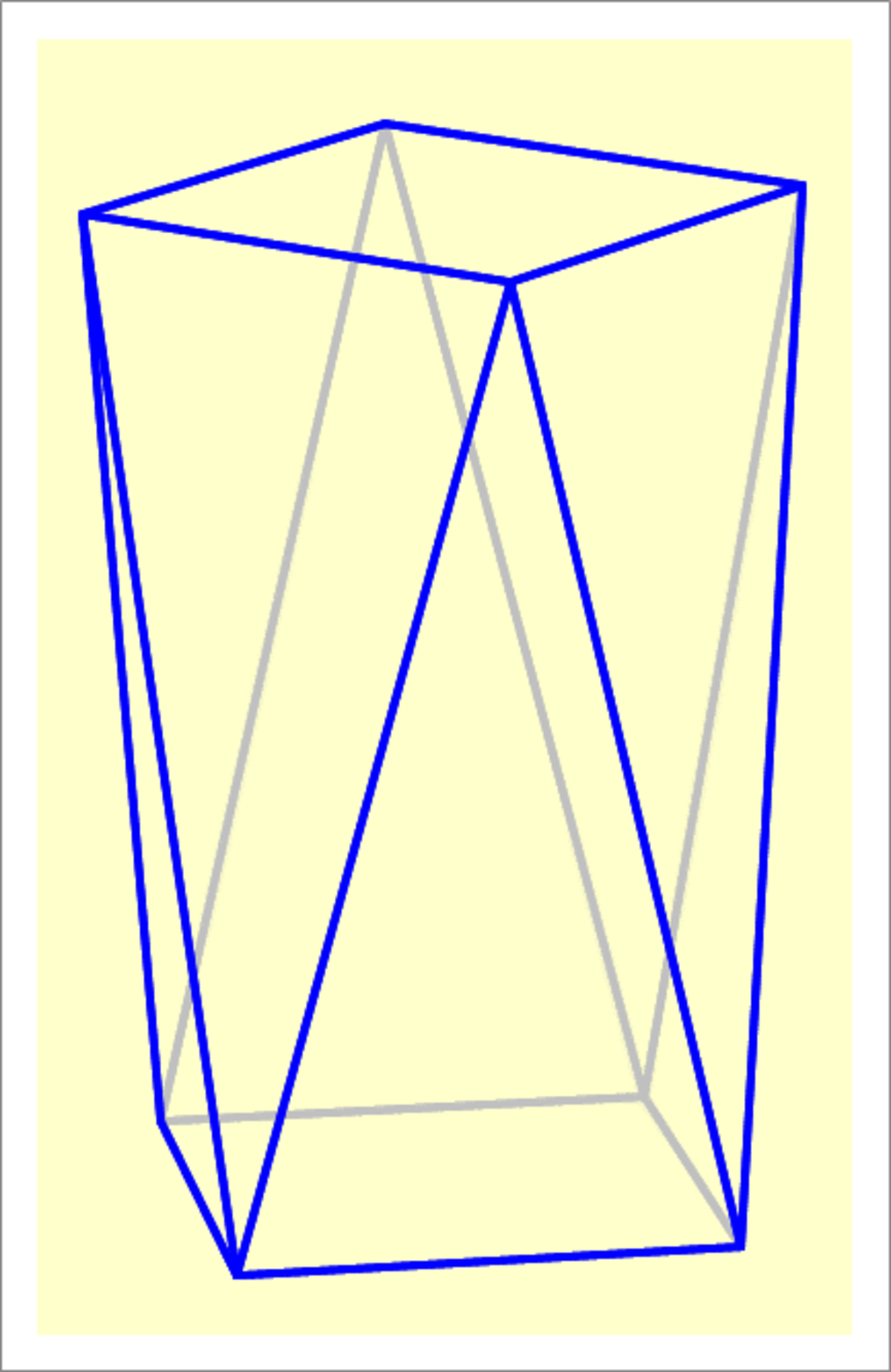
The answer is 2276.142375.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
My curiosity about this shape was greater than my efforts to research a formula. I tried a coordinate geometry approach.
From the definition of the shape, we can write down the coordinates of its eight vertices relative to an origin O at its centre:
| Point | x | y | z |
| O | 0 | 0 | 1 0 |
| A | − 5 2 | 0 | 1 0 |
| B | 0 | − 5 2 | 1 0 |
| C | 5 2 | 0 | 1 0 |
| D | 0 | 5 2 | 1 0 |
| E | − 5 | − 5 | − 1 0 |
| F | 5 | − 5 | − 1 0 |
| G | 5 | 5 | − 1 0 |
| H | − 5 | 5 | − 1 0 |
We can dissect the shape into two square pyramids O A B C D and O E F G H , and eight tetrahedra O A H E , O B E F , O C F G , O D G H , O A B E , O B C F , O C D G , O D A H .
The square pyramids each have volume V O A B C D = 3 1 0 0 0 .
To work out the volume of one of the tetrahedra (by symmetry, they all have the same volume), we use the absolute value of the determinant of the matrix of the coordinates of its three vertices (excluding the origin - this is analogous to the shoelace theorem in 2D):
V O A H E = ∣ ∣ ∣ ∣ ∣ ∣ 6 1 det ⎝ ⎛ − 5 2 − 5 − 5 0 5 − 5 1 0 − 1 0 − 1 0 ⎠ ⎞ ∣ ∣ ∣ ∣ ∣ ∣ = 6 5 0 0 ( 2 + 1 )
There are two square pyramids and eight tetrahedra; hence the overall volume is V = 2 × 3 1 0 0 0 + 8 × 6 5 0 0 ( 2 + 1 ) = 2 2 7 6 . 1 4 2 …
NB: a usable formula is here
By the way, if anyone could tell me how to format tables on here with internal column separators I'd really appreciate it!
Log in to reply
Like this? 1 6 2 7 3 8 4 9 5 1 0
Log in to reply
Yes - but is that using LaTeX or the table formatting option?
Oh, perhaps never mind - the table seems to be formatted OK now (though I don't know what changed - thank you if somebody edited it!)
Here's another idea - albeit with a hand-waving section. Using the coordinates above, the area of a cross-section of the solid parallel to the x y -plane is 5 0 ( 2 + 1 ) − 2 1 ( 2 − 1 ) z 2 where z ranges from − 1 0 to 1 0 . (These sections are square at the ends and octagonal in between.)
To find this area, note that the areas when z = ± 1 0 and z = 0 are easy to calculate. The area must be an even function in z , and - here's the hand-waving - must be a quadratic function - so this determines the function.
The volume is then found by integrating.
Thanks for the formula reference. I also agree with you that the area of the cross section is a quadratic function of the elevation z . And this leads to the formula, by direct integration. Thanks again for your insight.
The prismoidal formula for solids such as this (ruled frustra) tells us that the volume is V = 6 1 h [ A ( 0 ) + 4 A ( 2 1 h ) + A ( h ) ] where h is the highest of the solid and A ( z ) the cross-sectional area at height z . Thus A ( 0 ) = A ( h ) = 1 0 2 = 1 0 0 , while A ( 2 1 h ) is the area of a regular octagon of side length 5 , which is 5 0 ( 1 2 + 2 ) . Thus V = 6 2 0 [ 1 0 0 + 2 0 0 ( 1 + 2 ) + 1 0 0 ] = 3 2 0 0 0 ( 2 + 2 ) = 2 2 7 6 . 1 4 2 3 7 5
Imagine the solid as part of a square pyramidal frustum with 4 tetrahedrons lopped off. If the side of the top square is x , then by the properties of a right isosceles triangle the bottom side of one tetrahedron is 2 2 x , and the side of the bottom square of the frustum is 2 x .
Letting h be the height, the volume of the solid is then V = V frustrum − 4 V tetrahedron = 3 1 h ( x 2 + x ⋅ 2 x + ( 2 x ) 2 ) − 4 ⋅ 6 1 ⋅ 2 2 x ⋅ 2 2 x ⋅ h which simplifies to
V = 3 2 + 2 x 2 h
In this problem, x = 1 0 and h = 2 0 , so the volume is V = 3 2 + 2 ⋅ 1 0 2 ⋅ 2 0 = 3 2 0 0 0 ( 2 + 2 ) ≈ 2 2 7 6 . 1 4 2 3 7 5 .