There's infinitely many such polynomials!
Find a monic quartic polynomial with 4 distinct real roots, such that if we were to construct a triangle whose vertices are the polynomials' 3 turning points, the triangle formed is equilateral.
The area of this equilateral triangle can be expressed as 6 A , submit your answer as A .
The answer is 243.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
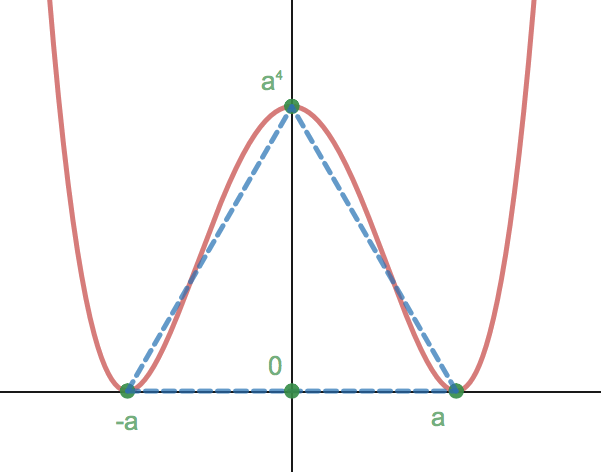 Consider, WLOG*, the monic quartic
y
=
(
x
2
−
a
2
)
2
.
Consider, WLOG*, the monic quartic
y
=
(
x
2
−
a
2
)
2
.
This quartic has turning points
(
±
a
,
0
)
,
(
0
,
a
4
)
.
For the points to form an equilateral triangle,
a
4
=
a
3
, i.e.
a
3
=
3
.
Area of triangle is given by
2
1
⋅
2
a
⋅
a
4
=
a
5
=
6
A
(given).
Hence
A
=
a
3
0
=
(
3
)
1
0
=
3
5
=
2
4
3
.
* This quartic has two real coincident roots at each of ( ± a , 0 ) but it can easily be converted to a monic quartic with four real distinct real roots with a simple vertical translation, and the analysis here would still hold.
But why must the monic quartic be y = ( x 2 − a 2 ) 2 ?
Log in to reply
It doesn't. It can be be any monic quartic that satisfies your conditions.
y
=
(
x
²
−
a
²
)
²
was chosen because it is symmetric and its turning points are obvious and simple. Imposing the equilateral triangle condition then determines the value of
a
, using which the the area can be calculated.
To satisfy the condition for four distinct real roots, the quartic is displaced negatively in the
y
direction. The relative positions of the three turning points (and hence the area of the triangle formed) remain unchanged.
Another way to think about it:
Set the three vertices of the equilateral triangle to be
(
±
a
,
0
)
,
(
0
,
a
3
)
.
Now find a quartic that has turning points at these vertices.
For
(
±
a
,
0
)
, we need coincident roots at these points, i.e.
y
=
(
x
−
a
)
2
(
x
+
a
)
2
=
(
x
2
−
a
2
)
2
, which is monic as required.
Fixing the third vertex gives
a
3
=
3
, and the rest of the solution follows.
Log in to reply
Beautiful!
Log in to reply
@Pi Han Goh
–
Thanks! :)
Nice question!
I have created an extension of it (sextic/pentagon) and posted it
here
.
Log in to reply
@Hypergeo H. – Yup, I saw your post and I'm already stumped!
Log in to reply
@Pi Han Goh – Try the second method above – fix the vertices first. To simplify things, choose the origin as the symmetrical vertex.
Log in to reply
@Hypergeo H. – Yup, I believed I got it. But I don't think my approach is rigorous. I'll continue to work on it until I'm sure it's rigorous.
This is a great problem! Looking forward to Symmetric Sextic. Thank you.
One example of a quartic polynomial with the given conditions is as follows:
The above graph can be shifted horizontally and vertically without changing the area of the triangle, so for convenient calculations, let's shift it so that the middle turning point is at the origin.
Then the quartic will have a double root at 0 and (since it must be symmetrical) two other roots at x = ± p , therefore giving it an equation y = x 2 ( x − p ) ( x + p ) = x 4 − p 2 x 2 for some real value of p .
The turning points are when its derivative is 0 , so 4 x 3 − 2 p 2 x = 0 , which solves to x = 0 and x = ± 2 2 p , and gives the turning points ( 0 , 0 ) and ( ± 2 2 p , − 4 1 p 4 ) .
Since the ratio of the height of an equilateral triangle to half its side is 3 , using the coordinates of the right turning point we have 3 = 2 2 p 4 1 p 4 , which solves to p = 6 2 4 .
Then the bottom side of the equilateral triangle is s = 2 2 2 p = 2 6 2 4 , so its area K = 4 3 s 2 = 4 3 ( 2 6 2 4 ) 2 = 6 2 4 3 . Therefore, A = 2 4 3 .