They look similar...(3)

You can use logarithms.

$x^{(x^x)}={(x^x)}^x\\x^x\log x=x\log(x^x)\\ x^x\log x=x^2\log x.$

If $x=1,\,\log x|_{x=1}=0$ . Supposing that $x\neq 1$ , where $x=1$ is one of the possible solutions, we have that

$x^x=x^2\Rightarrow x\log x=2\log x\Rightarrow x=2.$

Adding the solutions, we have that the answer of this question is $S=1+2=\boxed{3}.$

Plotting $y^x = x^y$ and $y = x^x$ produces only two solutions which can be quickly verified -- namely x = 1 and x = 2.

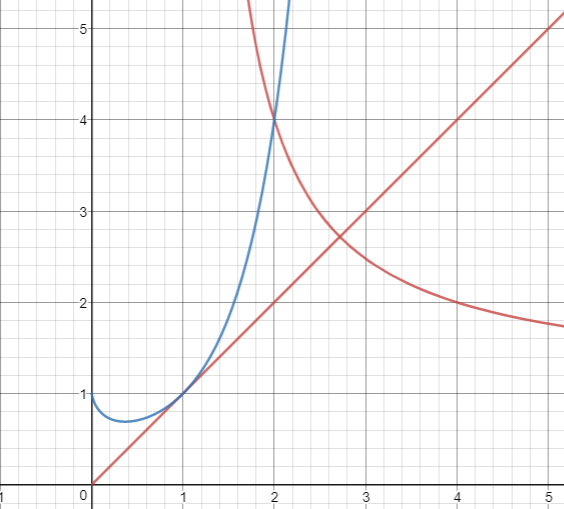
Hence the solution is 3.

$x^{(x^x)}=\left(x^x\right)^x$ $\implies x^{x^x}=x^{x^2}$ $\log_{x}x^{x^x}=\log_{x}x^{x^2} \begin{cases} \log_{x}x^{x^x}=\log_{x}x^{x^2} & ~x\not=0,~1 \\ \text{save for later} & ~x=0,~1 \\ \end{cases}$ $\implies x^x=x^2$ $\vdots$ $\implies x=2$

Now, take the two cases we excluded from the solution earlier and plug in 1 for $x$ : $1^{1^1}=1^{1^2}$ $1=1$

$0^0$ is undefined, so there's no point in checking. This gives the solution $1+2=3$ $~\beta_{\lceil \mid \rceil}$

$\begin{aligned} x^{x^x}&=(x^x)^x=x^{x^2} \\ x^x&=x^2 \\ x&=1,2 \end{aligned}$

Therefore, the sum of all $x$ 's is $3$ .

By the Desmos Theorem, the answer is 3.

If we observe then 1 holds.now if we do x^x^x=(x^x)^×then we get x^x^x=x^x^2.by comparing we get x=2.any thing greater than 2 will no hold.so sum of such x=1+2=3

Using common logic the condition can be satisfied only for the first two prime numbers and this can be easily be proved with logarithms When the equation is solved for x in the power the X =2 and then checking with x=1 also satisfies the condition... So 1+2= 3

Just intuition 😬

I don't see why x = -1 is not also a solution? So, why is it not 3 + 1 + (-1) = 2?

+1, -1 and 2 satisfy the criterion, therefore, 3=2+1 is the answer.

Answer=3

Since x>0 the only two possibilities are 1 and 2, hence their sum is 3 Apart from using logarithms and other solutions mentioned here, try plotting their graph and see the points of intersection for +be x........ just for fun:)

At first we shall take 1 as the possible value of x
So x=1
x^x^x=1^1^1=1;. x^x x=1^1 1=1;
If x=2;
x^x^x=2^2^2=2^4. 16.
x^x x=2^2 2=2^4=16
And if x=3
Then 3^3^3 is not equal to 3^3*3 hence
There is only 2 possible values of x that is 1 and 2 therefore there sum is 1+2 =3