Think!
n = 0 ∑ ∞ e n n 2
The value of above expression is in the form ( e − B ) C e ( A + e ) , where A , B and C are positive integers. Find A + B + C .
The answer is 5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
Log in to reply
Aah !! A very fast reply ! Thanks !!
By the way Nice problem !
Log in to reply
thanks :)
what are some tips for making more elegant solutions?
i'm not very good at that lol
Log in to reply
@Hamza A – You should check these Solution Writing Notes .
Log in to reply
@Akshat Sharda – thanks :)
and i hate why i can't just say thanks :)
you have to write more to publish it
and i did !:)
Nice solution!!
Great solution!
Consider:
n = 0 ∑ ∞ n 2 e − n x ⇒ n = 0 ∑ ∞ e n n 2 = n = 0 ∑ ∞ ∂ x 2 ∂ 2 e − n x See note. = ∂ x 2 ∂ 2 n = 0 ∑ ∞ ( e − x ) n Sum of infinite GP = ∂ x 2 ∂ 2 ( 1 − e − x 1 ) = ∂ x ∂ ( ( 1 − e − x ) 2 − e − x ) = ( 1 − e − x ) 2 e − x + ( 1 − e − x ) 3 2 e − 2 x Putting x = 1 = ( 1 − e − 1 ) 2 e − 1 + ( 1 − e − 1 ) 3 2 e − 2 = ( 1 − e − 1 ) 3 e − 1 + e − 2 = ( e − 1 ) 3 e ( e + 1 )
⇒ A + B + C = 1 + 1 + 3 = 5
Note: I learned this trick from Isaac Buckley . It is surely handy here.
Let the summation be equal to S then
S=0+ 1/e + 2^2 / e^2 + 3^3/e^3 + .......so on -(1) S/e= 1/e^2 + 2^2 /e^3 + .........so on - (2)
Subtract 1 from 2
S(1-1/e)= T = 1/e + 3/e^2 + 5/e^3........ (3)
Take LHS =T (new variable)
T/e = 1/e^2 + 3/e^3 ....... (4)
Subtract 3 from 4
T(1-1/e)= 1/e + 2[1/e^2 + 1/e^3 +........]
Then terms in square brackets can be solved by infinite GP formula ie a/1-r
====> (1/e^2)/(1-1/e) which is equal to 1/e(e-1)
Putting back and expressing T in terms of S we get on LHS S((e-1)^2/e^2)
And solving RHS we get (e+1)/(e.(e-1)) Equating We get
S= e(e+1)/(e-1)^3
A=1 B=1 C=3 A+B+C= 5
can you please use LaTeX?
Log in to reply
I don't actually know how to do it in latex . by the way I used algebra for it . you can try it .
Log in to reply
i can see that you did,i'm not noticing any errors so nice solution!
i may have the ability to see it(i used to be like you,not using LaTeX),but i found it very hard to write more advanced solutions on hard problems
i recommend this
https://brilliant.org/math-formatting-guide/
they have an app to download which converts equations to latex without you having to memorize it,i'm currently using it and it's really helpful
Log in to reply
@Hamza A – The guy above who has a Chinese name did it using latex his and mine is Same . The only thing being his is the more understandable one. But yeah thanks for the acknowledgement
I let you know how to use LaTeX in brilliant .
First, you have to use
\\\(\
, and `\)`.
If you want to use fractions, use this command,
\frac{numerator}{denominator}
.(Of course, you dont have to use {} if the one is one digit.)
Like 1 1 .
Next, if you want to use text, use
\text{write the text you want to write}
.
Third, other functions.
Like
\sin
,
\cot
,
\log_{base} number
,
\lim_{x \to number } the fraction expression
,
\infty
, etc.
Follow this link, How to format in brilliant .
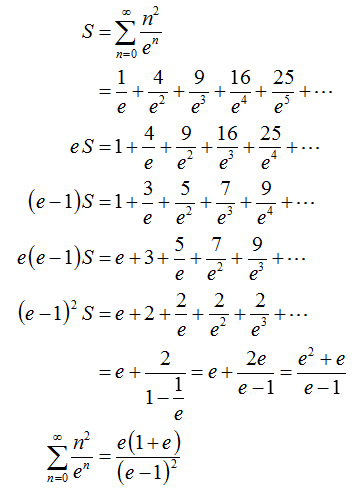
n = 0 ∑ ∞ x n n = 0 ∑ ∞ n x n − 1 n = 0 ∑ ∞ n x n − 1 n = 0 ∑ ∞ n 2 x n − 1 n = 0 ∑ ∞ n 2 x n − 1 = 1 − x 1 = d x d ( 1 − x ) − 1 = ( 1 − x ) 2 1 ⇒ n = 0 ∑ ∞ n x n = ( 1 − x ) 2 x = d x d x ( 1 − x ) − 2 = ( 1 − x ) 3 x + 1 ⇒ n = 0 ∑ ∞ n 2 x n = ( 1 − x ) 3 x ( x + 1 )
Placing x = e 1 ,
n = 0 ∑ ∞ e n n 2 = ( 1 − e 1 ) 3 e 1 ( e 1 + 1 ) = ( e − 1 ) 3 e ( e + 1 ) ⇒ 1 + 1 + 3 = 5