Think!
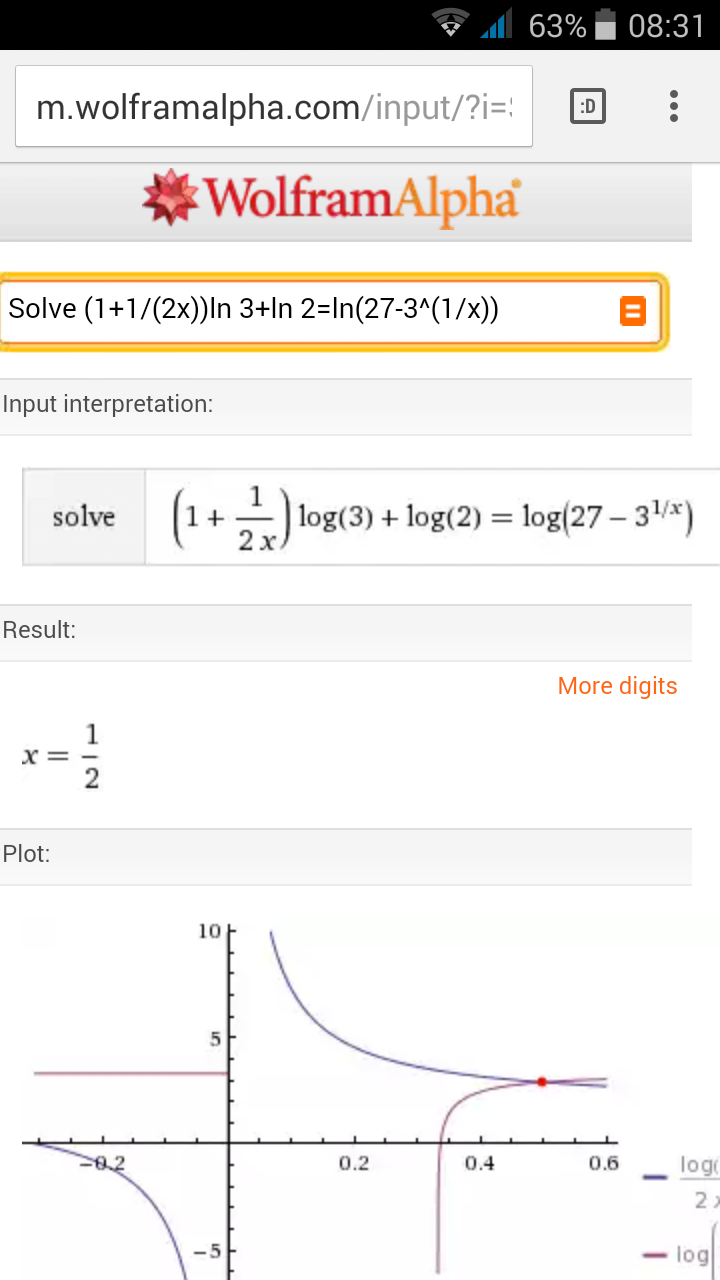
( 1 + 2 x 1 ) lo g 3 + lo g 2 = lo g ( 2 7 − x 3 )
Find the number of value(s) of x satisfying the equation above.
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
(May 30, 2021)
because x y = 1 / y x
1 / 2 3 = 3 1 / ( 1 / 2 ) = 3 2 = 9
So x = 2 1 is a solution.
Well x = 1 / 2 satisfy the given eqn.. So I guess you should make some edits in your solution and mention regarding the eqn having one solution.
Log in to reply
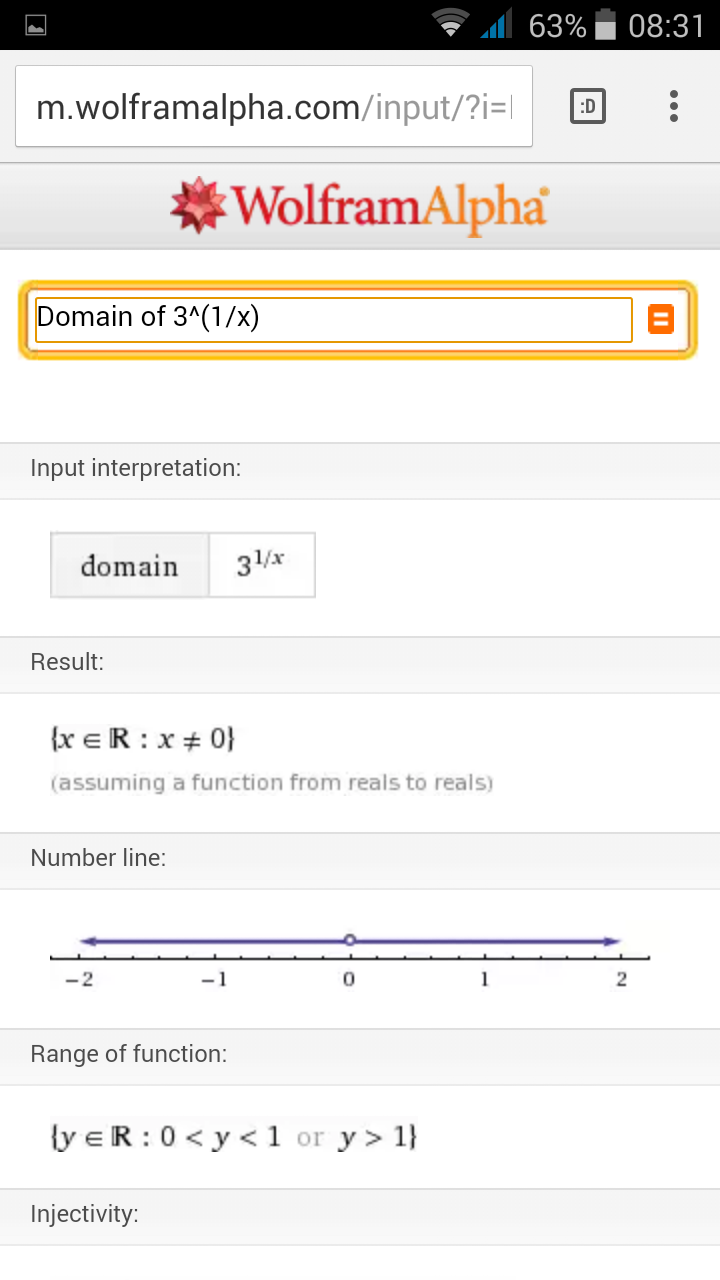
x 3 ⇒ x ∈ N , hence no solution!
Log in to reply
What??
Log in to reply
@Rishabh Jain – Although x 3 = 3 x 1 but still in our first expression we are given x 3 ⇒ x ∈ N .
If the question had ( 1 + 2 x 1 ) lo g 3 + lo g 2 = lo g ( 2 7 − 3 x 1 ) then 1 solution would be x = 2 1 .
Log in to reply
@Akshat Sharda – For a x , the exponential function for any a ∈ C , we don't have any restrictions like x ∈ N . If x is of form y 1 then this simply converts to y a .
If that is true, then why x a and a 1 / x are not synonymous to each other regarding the solutions for x .
I'm not sure I consider this a math question or a question about understanding notation. When I worked on the problem I converted the radical sign to 1/x and found there would be one solution without finding the solution. I wasn't aware that when using the radical symbol, the index needed to be a natural number. It does make sense. I decided to Google this. It took a long time to find a definition that said the index had to be a natural number. A lot implied it but didn't say it and many didn't mention it at all.
( 1 + 2 x 1 ) l o g ( 3 ) + l o g ( 2 ) = l o g ( 2 7 − ( 3 ) 1 / x ). Subtract l o g ( 2 ) from both sides and divide by l o g ( 3 )
( 1 + 2 x 1 ) = l o g 3 l o g ( 2 7 − 3 1 / x ) - l o g ( 3 ) l o g ( 2 )
l o g 3 l o g 2 = 1 . 5 8 5 ;
2 . 5 8 5 = l o g 3 l o g ( 2 7 − 3 1 / x ) - 2 x 1 ;
2 . 5 8 5 = l o g 3 ( 2 7 − 3 1 / x ) - 2 x 1 ;
2 . 5 8 5 = l o g 3 ( 3 3 ( 1 − 3 ( 1 / x ) − 3 )) - 2 x 1 ;
2 . 5 8 5 = 3 ( 1 − 3 ( 1 / x ) − 3 ) - 2 x 1 ;
From here, we can tell that there is no Natural value that satisfies the equation or there are 0 values in set N.
Moderator note:
(May 30, 2021)
because x y = 1 / y x
1 / 2 3 = 3 1 / ( 1 / 2 ) = 3 2 = 9
So x = 2 1 is a solution.
We have ( 1 + 2 x 1 ) × lo g 3 + lo g 2 = lo g ( 2 7 − x 3 )
lo g 3 + 2 x 1 × lo g 3 + lo g 2 = lo g ( 2 7 − x 3 ) lo g 6 + lo g 2 x 3 = lo g ( 2 7 − x 3 )
Put 2 x 3 = a , so x 3 = a 2
lo g 6 a = lo g ( 2 7 − a 2 ) a 2 + 6 a − 2 7 = 0 a 2 + 9 a − 3 a − 2 7 = 0 ( a + 9 ) ( a − 3 ) = 0 a = − 9 , 3 , but a = − 9 as a > 0 ⟹ x = 2 1 but x ∈ N for x 3 to be defined
Hence , The equation has no Solutions