Think Infinite
If the acceleration of topmost block is k g , find k .
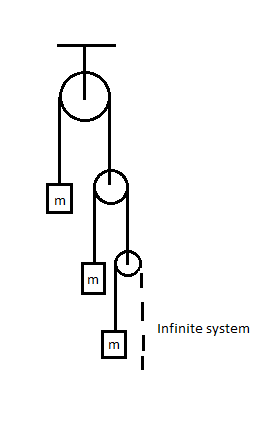
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution

Please explain your third line i.e T a 1 + 2 T a 2 + 4 T a 3 = . . . . = 0 ???
Log in to reply
That's something called the Virtual Work Method .
Log in to reply
You have posted a note i think .
Log in to reply
@Chirayu Bhardwaj – Yup, I had. I did not much from the note, but I reshared some problems whose solutions contained virtual work method.
Will you please explain it.
Log in to reply
@A Former Brilliant Member – I'm on tab, so I can't type LaTeX. But I'll surely take the opportunity to help you. Please view the solution to the following question.
Log in to reply
@Swapnil Das – The solution is of finite pulley system and I did it the same way Satvik Pandey has done but it didn't help me in this question How can we solve questions involving infinite pulley system
Log in to reply
@A Former Brilliant Member – I think the solution is enough for understanding. Where are you getting stuck?
Log in to reply
@Swapnil Das – I can't understand why T a 1 + 2 T a 2 + . . . . . is zero
Log in to reply
@A Former Brilliant Member – 1)For the topmost block, the forces acting are
Mg downwards and Tension T upwards...also it is moving with acceleration a1. a1=(T/m) - g
2) For the second block, the forces acting are
Mg downwards and Tension T/2 upwards...moving with acceleration a2. a2=(T/2m) - g ... ... ... This process continues infinitely... (I.e. Tension for third block is T/4, fourth block is T/8.......)
That's why the terms T/2, T/4, T/8... in the expression...
In pulley system, the sum of the product of acceleration and their respective tension is zero.....
Putting those values in the expression and solving with the help of infinite G.P., we get a1= g/2
Hope, this explanation is much clearer than what I had posted before..
@A Former Brilliant Member – That's virtual work for an infinite number of strings!
The "Rao IIT Academy" Symbol !!! This problem came in one of the recent Rao tests and I presume the problem's picked up from there!
Log in to reply
You're probably right. Therefore, the solution isn't original :P
Log in to reply
Actually, even I had written the test.
Log in to reply
@Miraj Shah – Yeah, I took It from the tests only... This question has a flavour of both Maths and physics..and interesting too.. That's why posted it..:)
Log in to reply
@Ganesh Iyer – Ya..its a good question!
@Ganesh Iyer – This question was famously posted by David Morin, in his perhaps, weekly physics challenges. Nice to relive the moment.