In square units, what is the area of this ellipse?
Here are the coordinates of three points on the ellipse:
( 3 . 1 5 6 7 4 , ( 2 . 1 9 1 5 7 , ( 2 . 8 0 6 5 4 , 3 . 4 9 6 6 5 ) 3 . 3 4 3 7 8 ) 2 . 5 8 4 3 5 )
You want the ellipse that passes through those three points which has the minimum area. That is the ellipse of which you want the area. Before you say that that is impossible to solve, please, read Steiner Ellipse, Minimal Area Through Three Points .
In the solution, I will demonstrate that the problem is a special case and therefore solve this problem two different ways.
2020-10-06T17:18Z : Texts of the commands that can used in Wolfram|Alpha Online added to the end on the solution.
The answer is 1.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Nice solution,btw pls give a solution for this .........(I think you have solved just now)
This reply is separately to both Chew-Seong Cheong and to Srijan Singh.
To Chew-Seong Cheong: the conversion factor you used comes from the ratio of the area of the enclosing circle to the area of the enclosed equilateral triangle that lays at the Steiner Ellipse problem.
To Srijan Singh: the answer is 0 . 5 Ω . It can be seen by inspection. The AD resistor is paralleled by the other five resistors, which are a balanced Whetstone bridge and therefore, there is no voltage across the CD resistor. This means that effectively the CD resistor is not there. Therefoer, the effective resistance of the Whetstone bridge is 1 Ω . Two paralleled 1 Ω is .... Of course, the problem gets much harder, if the resistors are not all the same.
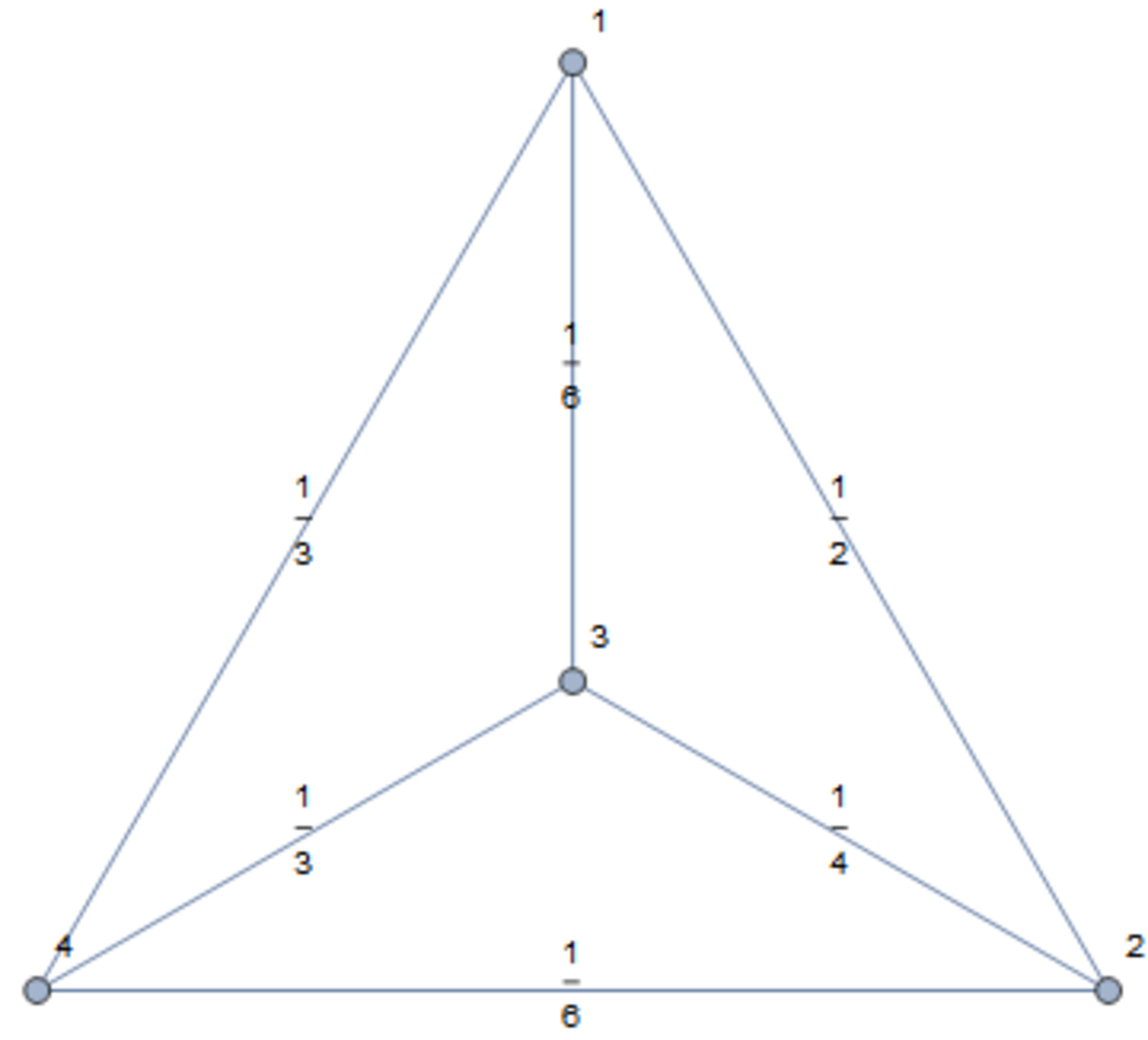
The graph's vertices are labeled by integers, instead of letters. The edges are labeled by the conductances (that is, the reciprocal of the resistance).
Using this method, writing in Wolfram Mathematica language: resistance = With [ { Γ = PseudoInverse [ With [ { wam = WeightedAdjacencyMatrix [ $#$1 ] } , DiagonalMatrix [ Tr /@ wam T ] − wam ] ] } , Outer [ Plus , Diagonal [ Γ ] , Diagonal [ Γ ] ] − Γ − Γ T ] & ; . The reistance matrix matrix is (yes, the output is in the reciprocal of the input):: ⎝ ⎜ ⎜ ⎛ 0 8 0 1 1 1 8 0 1 5 9 1 6 2 7 8 0 1 1 1 0 2 0 3 9 2 0 3 9 8 0 1 5 9 2 0 3 9 0 5 9 1 6 2 7 2 0 3 9 5 9 0 ⎠ ⎟ ⎟ ⎞ ≈ ⎝ ⎜ ⎜ ⎛ 0 . 1 . 3 8 7 5 1 . 9 8 7 5 1 . 6 8 7 5 1 . 3 8 7 5 0 . 1 . 9 5 1 . 9 5 1 . 9 8 7 5 1 . 9 5 0 . 1 . 8 1 . 6 8 7 5 1 . 9 5 1 . 8 0 . ⎠ ⎟ ⎟ ⎞
First, showing that this is a special case.
The Euclidean distances between the three points are equal and are 0.977205 each. Because it is an equilateral triangle, the Steiner ellipse is, in fact a circle. A circle is a special case of an ellipse, by the way. Therefore, the center of the triangle and of the circle is the average of the coordinates of the points' coordinates, { 2 . 7 1 8 2 8 , 3 . 1 4 1 5 9 } . Yes, I used π and e as the center's coordinates. The Euclidean distance to any of the points is 0 . 5 6 4 1 9 . The answer is π 0 . 5 6 4 1 9 2 ≈ 1 . 0 0 0 × 1 0 0 . See, that was easy! T M S t a p l e s
Ok, say that you did not see that the triangle was equilateral. Now, we will use the method in the wiki page mentioned in the problem statement. For the explanation of what is happening see that wiki page and the Singular Value Decomposition wiki page. o = ⎝ ⎛ 3 . 1 5 6 7 4 3 . 4 9 6 6 5 1 2 . 1 9 1 5 7 3 . 3 4 3 7 8 1 2 . 8 0 6 5 4 2 . 5 8 4 3 5 1 ⎠ ⎞ . n = ⎝ ⎛ 1 0 1 − 2 1 2 3 1 − 2 1 − 2 3 1 ⎠ ⎞ . a = n o − 1 = ⎝ ⎛ 1 . 3 7 7 4 6 − 1 . 1 1 5 4 4 0 1 . 1 1 5 4 4 1 . 3 7 7 4 6 0 − 7 . 2 4 8 5 7 − 1 . 2 9 5 3 2 1 . ⎠ ⎞ . Inverse of a gives the transformation function: ⎝ ⎛ 0 . 4 3 8 4 5 8 0 . 3 5 5 0 5 6 0 . − 0 . 3 5 5 0 5 6 0 . 4 3 8 4 5 8 0 . 2 . 7 1 8 2 8 3 . 1 4 1 5 9 1 . ⎠ ⎞ . The last column, first two rows, gives the center of the ellipse.
Doing the singular value decomposition of the first two rows and columns of the transformation function gives: u = ( − 1 . 0 . 0 . 1 . ) , σ = ( 0 . 5 6 4 1 9 0 . 0 . 0 . 5 6 4 1 9 ) , v ∗ = ( − 0 . 7 7 7 1 4 6 0 . 6 2 9 3 2 0 . 6 2 9 3 2 0 . 7 7 7 1 4 6 ) . From u , one can see that affine transform is considered to be a reflection. From σ , one can see the radii and that they are equal to each other and are 0 . 5 6 4 1 9 . From v ∗ , one can see, because it is a rotation matrix, that the rotation angle is 3 9 ∘ . Therefore, the area of the ellipse is π × 0 . 5 6 4 1 9 × 0 . 5 6 4 1 9 ≈ 1 . . ∴
The special case solution ought to be accessible to an advanced placement 9 t h or 1 0 t h (American) grade student. The general solution is second year or later university mathematics for a undergraduate student majoring in mathematics.
Clearly, this is not for 7~10th graders, right?
Log in to reply
Nope. This is university level kind of math.
Log in to reply
@Pi Han Goh @Half pass3 - it's a good challenge, though, right? Is there a way to explain the solution to this specific problem in a way that would be accessible?
Grades vary a bit by country but is it fair to say in grades 7-10 you've seen some coordinate geometry, including the equation of a circle, but no vectors/matrices or calculus? And I guess you'd know the area of an ellipse with semi-axes a and b is π a b .
Log in to reply
@Chris Lewis – Yes, if one spotted the special case nature of this problem. Therein, lies "the rub."
When one can find all of the "machinery" in Wolfram Alpha, yes. By the way, I was doing my baby sitter's math homework for her when I was in third grade and she was in ninth grade and that included multiple equations in multiple unknowns algebra problems. I did not understand why she found it so hard. I did not know that I was not supposed to be able to do that then. Oops.
Log in to reply
What exactly would you enter into Wolfram|Alpha to find this if you weren't familiar with matrices? I'm genuinely curious if there's a way to use Alpha like this. Typing in "smallest ellipse through three points" I get "Using closest Wolfram|Alpha interpretation: three points", which isn't very helpful!
Google gets you straight to the article you linked, but again, without familiarity with matrices it's pretty opaque.
There have been a few problems on here lately using Steiner ellipses (and Steiner inellipses) - it would be interesting to know (as per my reply above) whether there is a more elementary way to get at this question, especially in this equilateral case.
Log in to reply
If you are not familiar with matrices, then it would be difficult but possible in Wolfram|Apha as you would be redeveloping matrix algebra by yourself. Ouch.
Using Wolfram|Alpha online (so that I can cut-and-paste):
{1.,-0.5,-0.5},{0.,0.866025,-0.866025},{1.,1.,1.}} inverse({{3.15674,2.19157,2.80654},{3.49665,3.34378,2.58435},{1,1,1}})
which gives ⎝ ⎛ 1 . 3 7 7 4 6 − 1 . 1 1 5 4 5 0 1 . 1 1 5 4 4 1 . 3 7 7 4 6 0 − 7 . 2 4 8 5 8 − 1 . 2 9 5 3 1 1 ⎠ ⎞
inverse({{1.37746, 1.11544, -7.24858},{-1.11545, 1.37746, -1.29531},{0, 0, 1}})
which gives ⎝ ⎛ 0 . 4 3 8 4 5 6 0 . 3 5 5 0 5 6 0 − 0 . 3 5 5 0 5 3 0 . 4 3 8 4 5 6 0 2 . 7 1 8 2 8 3 . 1 4 1 5 9 1 ⎠ ⎞
singular value decomposition({{0.438456,-0.355054},{0.3550564`,0.438456}})
which gives M = U . Σ . V † where M = ( 0 . 4 3 8 4 5 6 0 . 3 5 5 0 5 6 − 0 . 3 5 5 0 5 4 0 . 4 3 8 4 5 6 ) U = ( 0 . 4 3 0 5 1 1 0 . 9 0 2 5 8 5 0 . 9 0 2 5 8 5 − 0 . 4 3 0 5 1 1 ) Σ = ( 0 . 5 6 4 1 8 9 0 0 0 . 5 6 4 1 8 7 ) V = ( 0 . 9 0 2 5 8 5 0 . 4 3 0 5 1 1 0 . 4 3 0 5 1 1 − 0 . 9 0 2 5 8 5 )
Then, go look at the general solution.
The Steiner ellipse is an ellipse with the least area that touches a triangle at its three vertices. And its area is A S = 3 3 4 π A △ , where A △ is the area of the triangle.
To find A △ from its three vertices A ( 3 . 1 5 6 7 4 , 3 . 4 9 6 6 5 ) , B ( 2 . 1 9 1 5 7 , 3 . 3 4 3 7 8 ) , and C ( 2 . 8 0 6 5 4 , 2 . 5 8 4 3 5 ) , we use the formula below:
A △ ⟹ A S = ∣ ∣ ∣ ∣ 2 A x ( B y − C y ) + B x ( C y − A y ) + C x ( A y − B y ) ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ 2 3 . 1 5 6 7 4 ( 3 . 3 4 3 7 8 − 2 . 5 8 4 3 5 ) + 2 . 1 9 1 5 7 ( 2 . 5 8 4 3 5 − 3 . 4 9 6 6 5 ) + 2 . 8 0 6 5 4 ( 3 . 4 9 6 6 5 − 3 . 3 4 3 7 8 ) ∣ ∣ ∣ ∣ ≈ 0 . 4 1 3 4 9 4 7 5 9 = 3 3 4 π A △ ≈ 1 . 0 0