Point In Square
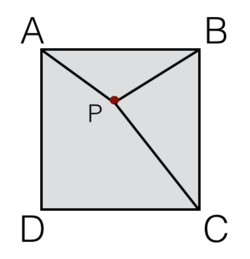A
B
C
D
is a square that contains point
P
such
that
P
A
:
P
B
:
P
C
=
1
:
2
:
3
. Find
∠
A
P
B
in degrees.
The answer is 135.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
There's a typo in here. Actually, lCPl=3 (Not BP) and CP²=(CP')²+(P'P)² which makes angle CP'B = 90°.
can u provide picture or diagram of ur solution?
Let the side is "S", and angle CBP = θ, then angle PBA = 90 - θ.
To make it simple, we take PA = 1, PB = 2, PC = 3.
Using cosines law, we find
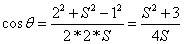and
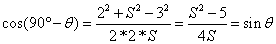
And then because
,
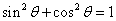we can find
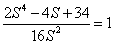(Sorry for typo in equation !)
We get
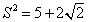
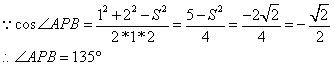
Brilliant method!
When you calculate S 2 , why can't S 2 = 5 − 2 2 ?
Log in to reply
I think he made a mistake in his calculation. It should be 1 6 S 2 2 S 4 − 4 S 2 + 3 4 .
Let A = S 2 , therefore, 1 6 A 2 A 2 − 4 A + 3 4 = 1 . Then you can obtain the result of A = 5 ± 2 2 = S 2 by solving the quadratic equation.
Log in to reply
I realized that part. But which one do you pick?
Log in to reply
@Thinula De SIlva – Oops... I read the question incorrectly... :(
5 − 2 2 < 3 means that the side length S is not going to be 5 − 2 2 .
Assume point P to be at (a,b) with A:(0,0), B:(s,0) & C:(s,s). Now we can say: a² + b² = p², (s-a)² + b² =4p² and (s-a)²+(s-b)² = 9p² which yield p=a√(7-4√2) & s=(3√2 -1)a. So we've PA=a√(7-4√2), PB=2a√(7-4√2) and AB=(3√2 -1)a. Apply cosine rule to triangle PAB to get /_APB=135°
how can you say a^2 + b^2 = p^2?
Log in to reply
This is just an application of the distance formula which is nothing but the Pythagoras Theorem.
Let's take point P' out of the square such that triangle APB is congruent to triangle CP'B. So we get angle ABP= angle CBP' => angle PBP'=90 => the traingle PBP' is a isosceles right triangle => |PP'|=2root2 and |CP'|=1 and |BP|=3 => angle CP'P=90=> angle CP'B= angle APB=90+45=135