This should be easy! Right?
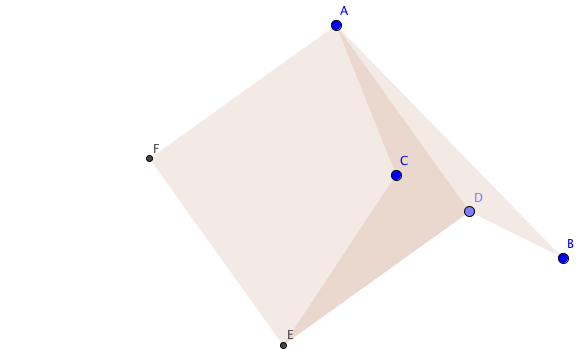
△ A B C is a triangle such that A C = 1 3 units, A B = 2 0 units and B C = 1 2 units. D is a point on BC such that B D = D C . A square A D E F is drawn with a side A D .
If the area of the triangle C D E is equal to H G unit 2 , where G and H are coprime positive integers, find G + H .
The answer is 239.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Akshay Yadav , do you want me to put the image in the problem? Popular problem often have pictures!
Log in to reply
Ok. You can do that.😁
Log in to reply
Done! How does it look now?
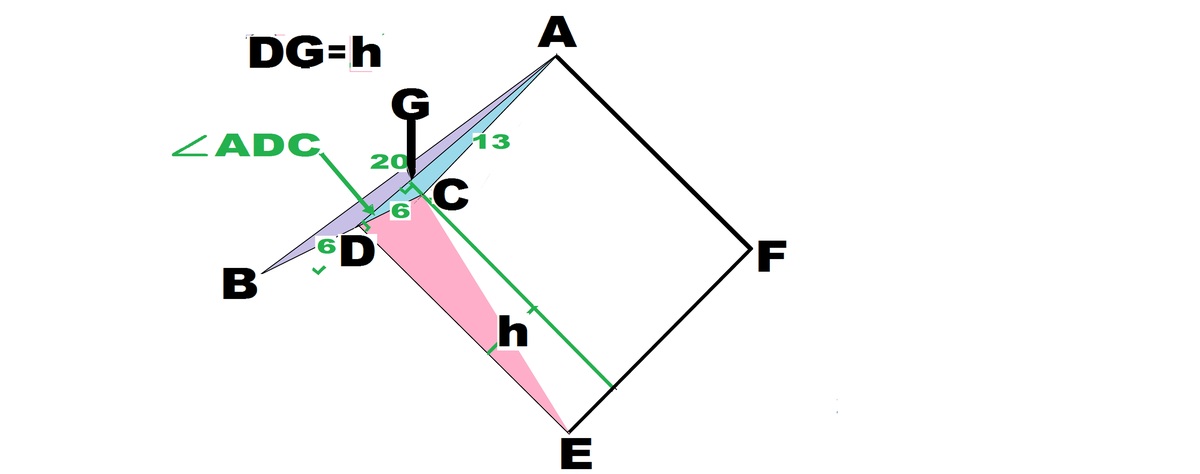
First we find the median A D using the formula A D = 2 2 ( A C 2 + A B 2 ) − B C 2 .
Then A D = 2 2 ( 1 3 2 + 2 0 2 ) − 1 2 2 = 2 9 9 4 . Now let θ = ∠ A D C , then ∠ C D E = 9 0 ∘ − θ , also A D = D E .
Using Law of cosines we get cos θ = 2 ⋅ C D ⋅ A D C D 2 + A D 2 − A C 2 = 2 ( 6 ) ( 2 9 9 4 ) 6 2 + ( 2 9 9 4 ) 2 − 1 3 2 = 4 9 9 4 7 7 .
Finally, [ C D E ] = 2 1 C D ⋅ D E ⋅ sin ( 9 0 ∘ − θ ) = 2 1 ( 6 ) ( 2 9 9 4 ) ( 4 9 9 4 7 7 ) = 8 2 3 1 .
So the answer is 2 3 1 + 8 = 2 3 9 .
I did it the same way.
A D 2 = 4 1 ∗ ( 2 ∗ A B + 2 ∗ A C 2 − B C 2 ) = 2 4 9 7 . B D = D C = 6 . C o s A D C = 2 ∗ A D ∗ 6 A D 2 + 6 2 − 1 3 2 A r e a o f Δ C D E = 2 1 ∗ A D ∗ h . B u t h = D C ∗ C o s A D C . A r e a Δ C D E = 2 1 ∗ A D ∗ D C ∗ 2 ∗ A D ∗ 6 A D 2 + 6 2 − 1 3 2 . A r e a Δ C D E = 2 1 ∗ 6 ∗ 2 ∗ 6 2 4 9 7 + 6 2 − 1 3 2 = 8 2 3 1 . A r e a Δ C D E = H G . ∴ G + H = 2 3 9
Refer to the image above.
We deduce that B D = D C = 6 .
by the cosine law 2 0 2 = 1 2 2 + 1 3 2 − 2 ∗ 1 2 ∗ 1 3 cos ( C ) ⟹ cos ( C ) = 1 0 4 − 2 9 Let the lenght of the sqare be a Consider it to be a lenght of the triangle 6 , 1 3 , a .It has the same angle as the big triangle! By the cosine law: a 2 = 6 2 + 1 3 2 − 2 ∗ 6 ∗ 1 3 cos ( C ) = 2 4 9 7 ⟹ a = 2 4 9 7 Consider the angle opposite to the side 13 in the small triangle. let it be A .Using the cosine law again: 1 3 2 = 6 2 + 2 4 9 7 − 2 ∗ 6 2 4 9 7 cos ( A ) ⟹ A = arccos ⎝ ⎜ ⎜ ⎛ 4 1 1 1 4 2 7 ⎠ ⎟ ⎟ ⎞ Since a square makes 2 π angle between each sides, the angle adjacent to A is 2 π − A . We know the value of the two sides required for the formula of the area(the sides of a square are equal) area = 2 1 ∗ 6 ∗ 2 4 9 7 ∗ sin ⎝ ⎜ ⎜ ⎛ 2 π − arccos ⎝ ⎜ ⎜ ⎛ 4 1 1 1 4 2 7 ⎠ ⎟ ⎟ ⎞ ⎠ ⎟ ⎟ ⎞ = 2 1 ∗ 6 ∗ 2 4 9 7 ∗ cos ⎝ ⎜ ⎜ ⎛ arccos ⎝ ⎜ ⎜ ⎛ 4 1 1 1 4 2 7 ⎠ ⎟ ⎟ ⎞ ⎠ ⎟ ⎟ ⎞ = 2 1 ∗ 6 ∗ 2 4 9 7 ∗ 4 1 1 1 4 2 7 = 8 2 3 1 2 3 1 + 8 = 2 3 9