This triangle is arbitrary so how do we determine the circumradius?

Let D and E be the centers of circles $\Gamma_1$ and $\Gamma_2$ .

and F be the center of circumscribed circle of $\Delta ABC$ .

We can see that triangles $\Delta AFD$ and $\Delta AEF$ are similar.

then: $\frac {AD}{AF} = \frac {AF}{AE}$ so that $R^2 = AF^2 = AD \times AE = 12 \times 15 =180$

Freehand Diagrams for the win!

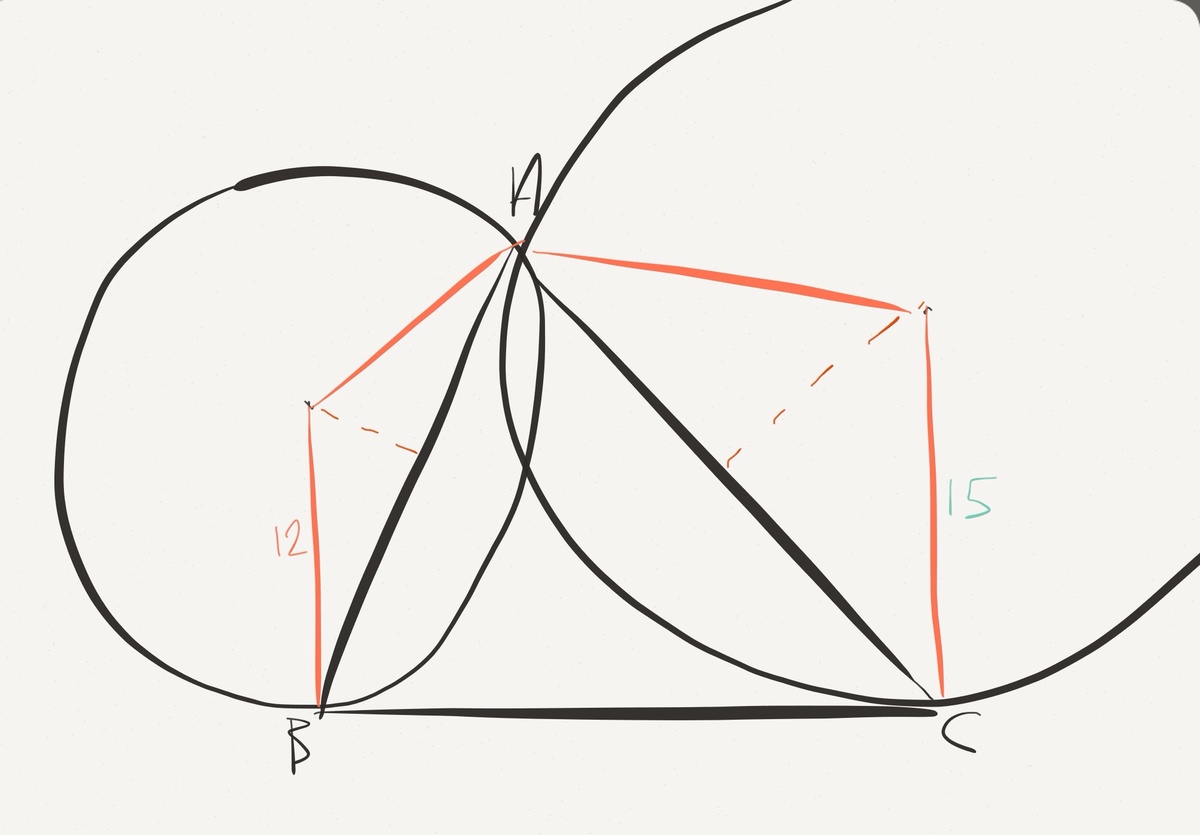
Split the isosceles triangles as shown in the diagram and we find that the angles are $90-B$ and $90-C$ . Therefore $b=2\times 15\sin C$ and $c=2\times 12 \sin B$ . Multiply the equations together and rearrange giving: $\frac{b}{2\sin B}\times \frac{c}{2\sin C}= 180$

But $\frac{b}{2\sin B}=R$ and $\frac{c}{2\sin C}=R$ so $R^2=180$ , $R=6\sqrt{5}$ and therefore the answer is $\boxed{11}$ .