This year is always better than last year?

The number of intersection points of the diagonals in a regular $n$ -sided polygon is based on $\dbinom{n}{4}$ , because every set of four vertices determines six edges and/or diagonals, but only one pair of those six lines intersects inside the polygon (see example in left image below.)

The problem with this simple count is that it is possible for more than two diagonals to intersect at one point, as the octagon on the right above shows. It turns out this only happens with even $n$ , so for odd $n$ the number of intersections is exactly $\dbinom{n}{4}$ . For even $n$ there are several correction factors, depending on whether the numbers $2, 4, 6, 12, 18, 24, 30, 42, 60, 84, 90, 120$ and/or $210$ are factors of $n$ . A very long formula and an even longer proof are given in this MIT paper . $\\ \\$

Since the only prime factors of $2018$ are $2$ and $1009$ , there is only one correction factor, which turns out to be $\dfrac{-5n^3 + 45n^2 - 70n + 24}{24}$

For $n=2018$ , this works out to be $-1704443159$ . So

• $f(2017) = \dbinom{2017}{4} = 687574403880 \\$
• $f(2018) = \dbinom{2018}{4} - 1704443159 = 687235550401 \\$

Thus $f(2017) > f(2018)$ .

It seems reasonable that with 2017 being prime that it might have more crossings because there will be fewer that coincide. It even happens for small primes: $f(12)<f(11)$ Some relevant lines of Number of intersections of diagonals in the interior of regular n-gon.

2016 684480896065

2017 687574403880

2018 687235550401

Note how small f(2016) is with all of its factors.

None of the mentioned solutions are sufficiently self contained, so here's a sufficiently self contained solution.

As Zico mentioned, solution is based on $n \choose 4$ because every quadruplet of points results in exactly one pair of intersecting diagonals. So, if we had to count the intersecting pairs of diagonals, we are done. But we have to count the intersections and the problem with that is different pairs of diagonals can intersect at the same point. But still, the above arguments shows that,

$f(n) \leq {n \choose 4}$

For the solution we need 2 facts -

1) For large primes (that is including 2017, which is a prime), this is an equality.

2) The correction for even sided polynomials is large enough to overcome the increase in $n \choose 4$ .

Roughly the argument will be that for large $n$ ,

${n \choose 4} \sim \frac{n^4}{24}$

so, ${(n+1) \choose 4} - {n \choose 4} \sim \frac{n^3}{6}$

We'll show that for large even $n$ ,

${n \choose 4} - f(n) \gtrsim \frac{5n^3}{24}$

So, for large enough even $n$ , the correction for even sided polynomials is large enough to overcome the increase in $n \choose 4$ .

For the first claim, that is for large primes (that is including 2017, which is a prime), this is an equality, I'm going to use notations from the figure 2 and corresponding analysis (which uses nothing more that similar triangles and basic properties of triangles and circles) in paper . The analysis I need out of the paper is VERY simple and I'm using that only to same myself some trouble of copying figure and analysis from there.

The equation we need is $\sin(u/2) \sin(v/2) \sin(w/2) = \sin(x/2) \sin(y/2) \sin(z/2)$ . Now it's clear that by writing $sin$ s in terms of exponential, for prime $p$ sided polygon, we can obtain a polynomial relation followed by the primitive $2p$ -th root of unity. Even without writing down the polynomial, we can see that it should be a non-constant polynomial with $<16$ terms, $<2p-3$ degree and rational coefficients. But by the irreducibility of cyclotomic polynomial $\Phi_{2p}(x)$ , for any $p \geq 17$ , we know such polynomial can't exist. So, $f(p) = {p \choose 4}$ for prime $p \geq 17$ . QED

In reality, as mentioned in the paper, this equality holds for all odd inputs but we don't need that.

For the second claim, for even $n$ , let's lower bound the number of triplets of diagonals intersecting at same point. In naive counting each triplet is 3 times, so correction factor will be double of number of triples. One trivial kind of solution to $\sin(u/2) \sin(v/2) \sin(w/2) = \sin(x/2) \sin(y/2) \sin(z/2)$ can be obtained by considering $u$ , $v$ and $w$ as permutations of $x$ , $y$ and $z$ . We can consider 2 cases -

1) one diagonal is passing through center - first choose a diagonal passing through center ( $\frac{n}{2}$ number of choices), now choose a point on one side of it ( $\frac{n-2}{2}$ number of choices), then point on other side which is not opposite or reflection to the point the first side (at least $\frac{n-6}{2}$ number of choices). The above two points makes the second diagonal and the reflection of it makes the third diagonal, note that because of reflection each triplet is counted twice,

Total trivial solutions in this case $\geq\frac{n(n-2)(n-6)}{16}$

So respective correction $\geq\frac{n(n-2)(n-6)}{8}$

2) no diagonal are passing through center - this is possible only if the circle is divided into $x,\ x,\ y,\ y,\ z,\ z$ arcs and $x$ , $y$ , $z$ are distinct. One example is shown in figure 3 in paper . Now splitting $\frac{n}{2}$ in 3 parts, not necessarily distinct, is ${{\frac{n}{2}-1} \choose {3-1}} = \frac{(n-2)(n-4)}{8}$ . And splits where at least 2 of $x$ , $y$ or $z$ are equal can't exceed $3(\frac{n}{2} - 1)$ . Now for the first vertex there are $n$ choices to make a triplet but every triplet will be counted thrice because of cycles of $x$ , $y$ , $z$ . So,

Total trivial solutions in this case $\geq\frac{n(n-2)(n-16)}{24}$

So respective correction $\geq\frac{n(n-2)(n-16)}{12}$

Adding the above two -

correction $\geq\frac{5n(n-2)(n-10)}{24}$

Which is, as mentioned earlier, $\sim \frac{5n^3}{24}$ .

Finally, by the above results,

As $2017$ is a prime greater than $17$ , so $f(2017) = {2017 \choose 4} = 687574403880$

And $f(2018) \leq {2018 \choose 4} - \frac{5*2018(2018-2)(2018-10)}{24} = 688939993560 - 1701900480 = 687238093080$

So, $f(2018) < f(2017)$

For comparison, as mentioned by Zico, $f(2018) = 687235550401$ so my approximation is off by $0.00037\%$ .

The polygon with $2017$ sides has $687574403880$ intersection points

The polygon with $2018$ sides has $687235550401$ intersection points

Sure isn't immediately obvious that $f(2n-1) > f(2n)$ , which is apparently true for all $n>8$

Here's the formula for $f(n)$ reprinted for the benefit of readers

$\dfrac { n! }{ 4!(n-4)! } +\frac { 1 }{ 24 } \left( -5{ n }^{ 3 }+45{ n }^{ 2 }-70n+24 \right) { \delta }_{ 2 }(n)$

$-\frac { 3 }{ 2 } n{ \delta }_{ 4 }(n)+\frac { 1 }{ 6 } \left( -45{ n }^{ 2 }+262n \right) { \delta }_{ 6 }(n)$

$+42n{ \delta }_{ 12 }(n)+60n{ \delta }_{ 18 }(n)+35n{ \delta }_{ 24 }(n)-38n{ \delta }_{ 30 }(n)-82n{ \delta }_{ 42 }(n)$

$-330n{ \delta }_{ 60 }(n)-144n{ \delta }_{ 84 }(n)-96n{ \delta }_{ 90 }(n)-144n{ \delta }_{ 120 }(n)-96n{ \delta }_{ 210 }(n)$

where $\delta_m (n)$ = $1$ if $n \; (Mod \: m)$ $=0$ , otherwise $\delta_m (n)$ = $0$

Once we have this formula $f(n)$ , it can be shown that $f(2n-1)>f(2n)$ for all $n>8$ . First, we find the difference
$f(2n-1)-f(2n)$ where we leave off all the correction factors $\delta_{m}$ for $m>6$ , setting up four equations for cases where $\delta_4,\delta_6$ each have a value of either $1$ or $0$ . The rest of the correction factors have a maximum value of $137 \cdot 2n$ which we subtract from this difference. Then we set each of the equations to $0$ and solve for $n$ , and find $n$ has the maximum value of $46.055$ , so that we know that $f(2n-1)>f(2n)$ for $n>46$ . Through checking the rest from $n=3$ to $n=46$ , we find that there are no counter examples after $n>8$ , and the rough proof is done.

A polygon with an odd number of sides will always have more diagonal intersections in respect to its number of angles. There's a good reason for this. With a polygon with and even number of sides, each point will always have exactly one other point directly across each other (cite this octagon to show how many each point connects to another here: 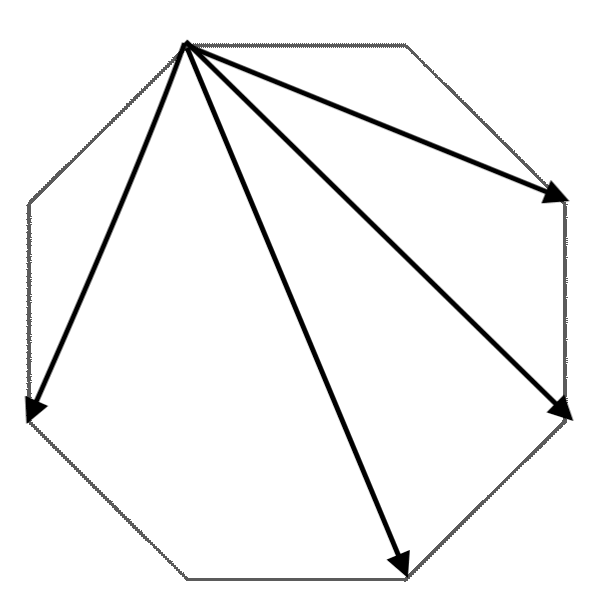). However, with an odd number of sides, one vertex will connect to one point more that the rest (See the heptagon here:

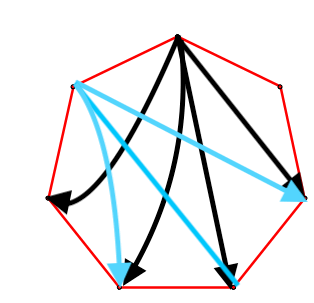
). This should mean the same for the dokiloheptdecagon and dokilooctdecagon (That's my guess as to what they should be called). Yes, I just imagine a heptagon and octagon.

I don’t usually resort to this kind of thinking, but it sometimes works for multiple choice questions. This involves no maths what so ever, and maybe using this method every now and then is useful when you’re utterly clueless as to what to do.

Essentially, it’s process of elimination. The answer can’t be ‘they are the same’ because adding more edges definitely changes the amount of intersections. Once this is out the way, your in game of luck, with a 50/50 chance of getting it right. But wait, there’s a catch. The person writing this question isn’t going to make the answer intuitive and obvious, because why would they write the question otherwise. At first I was thinking ‘surely it’s the second one’, but then I thought ‘no, can’t be. Too obvious’. And so I thought it has to be the non-intuitive answer: the first choice.

Try it sometime; you never know, it might work (don’t resort to this all the time though, becuase it’s not real maths!).