Three colors

Probability Level pending

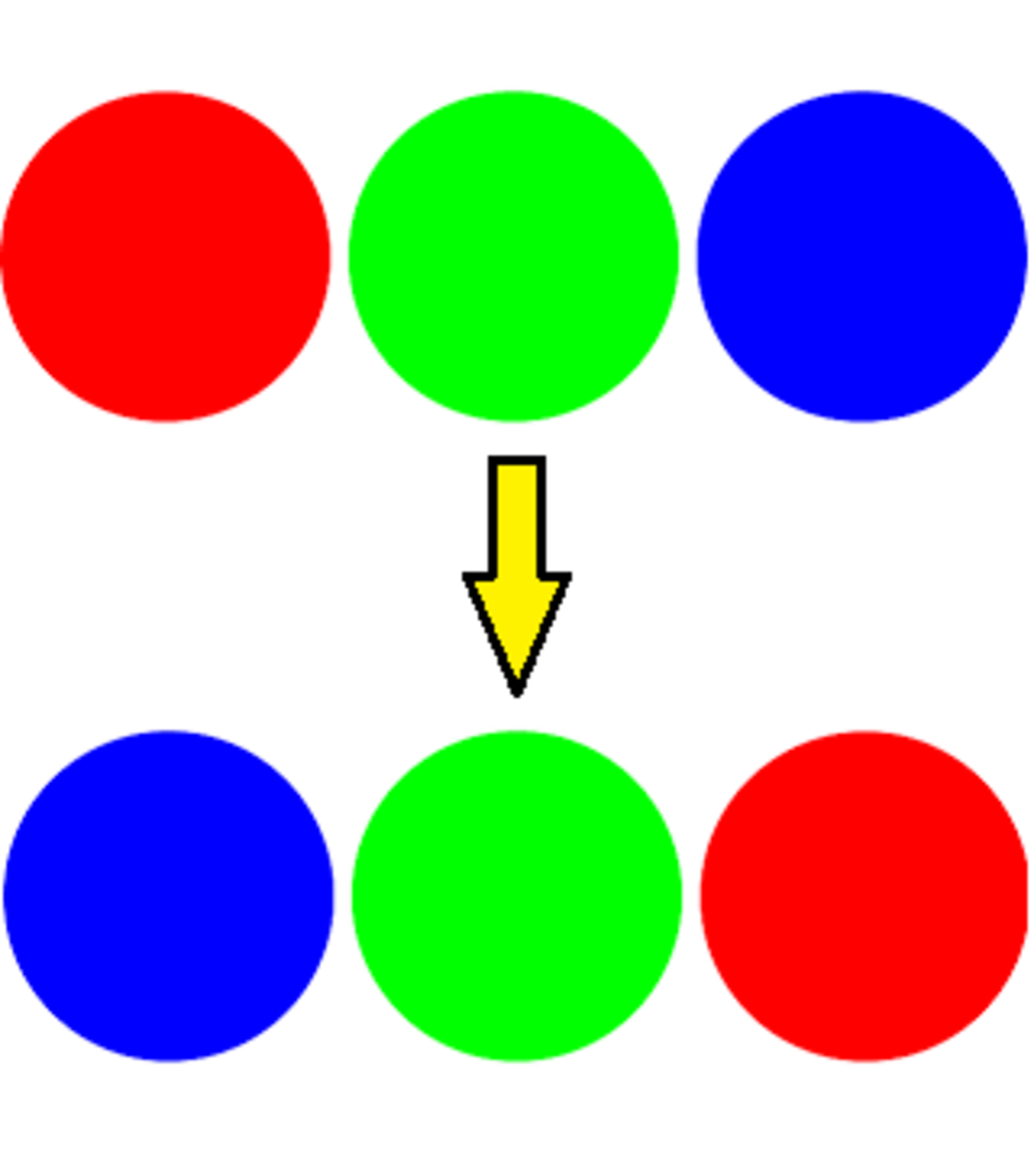
Three circles arranged in a row, start in the order $\color{#D61F06}red \color{#333333}\to \color{#20A900} green \color{#333333} \to \color{#3D99F6} blue$ .

Every move, two circles are randomly switched.

What is the expected number of moves before the circles are in the order $\color{#3D99F6} blue \color{#333333} \to \color{#20A900} green \color{#333333} \to \color{#D61F06} red$ .

1 None of these answers 7 5 6 4 2 3

1 solution

Geoff Pilling
Mar 6, 2017

There are three states to consider:

1) All the circles in the final order ( $blue \to green \to red$ )
2) One circle in the right place
3) None of the circles in the right place

Let $E_n =$ The expected number of moves to get from state $n$ to state 1

If you are in state 2, you have a $\frac{2}{3}$ chance of going to state 3 and a $\frac{1}{3}$ chance of going to state 1.

So, $E_2 = 1 + \frac{2}{3}E_3$ .

If you are in state 3, the next move you will be in state 2, so,

$E_3 = 1 + E_2$ .

Solving, $E_2 = \boxed5$

Great problem and solution. I started with $3! = 6$ states, one of which was the final state, and thought I was going to end up solving a system of 5 equations/5 unknowns, but found the system collapsed down to the same one you have. If I had to make a quick guess before doing the math I would have guessed 5, (and 6 if none of the circles were in the right place), so for once intuition lined up with reality.

Now if we were to add a yellow circle .... :) I guess we would have to add the state where two circles were in the right place, giving us a system of three equations. I'll give this a try when I have the time.

Brian Charlesworth - 4 years, 3 months ago

Interesting... Also with a fourth color it seems that there are a couple of ways to have no colors in the right place. Two switched and the other two switched, or a cyclic rotation... Hmmmm...

Geoff Pilling - 4 years, 3 months ago

Yes, that would be the complicating factor. For a given starting sequence, there are (i) 6 sequences that have two circles out of place compared to the original, (ii) 8 sequence that have three circles out of place and (iii) 9 sequences that are derangements of the original. The sequences in (i) and (ii) respectively can be dealt with in the same way, but as you point out, the derangements come in two flavors: pair-switching, of which there are 3, and the other 6 which are cyclic. So would we then have a system of 4 equations to deal with, or would there be further complications? And this is just with 4 circles; I can't even imagine trying to generalize this for $n$ circles. :p

Brian Charlesworth - 4 years, 3 months ago

@Brian Charlesworth – Haha... Generalizing for n circles, now there's a thought... But where to begin? Hmmmmmm... Is there a simpler way to do this than counting loop combinations etc... Perhaps a recursive way?

Geoff Pilling - 4 years, 3 months ago

@Geoff Pilling – Also, (going back to 4 circles), can all four way cycles be treated equally? (i.e. as one state)

Geoff Pilling - 4 years, 3 months ago

Three colors

1 solution

0 pending reports