Three of a kind!
Three friends, Slim, Jim, and Tim, each hold three cards—an ace, a two, a three—in a random order.
There are three turns and, on each turn, they simultaneously flip over a card face up, as illustrated below (without returning the card to their hands).
The probability that there's a three-way match on at least one of the flips is b a , where a and b are coprime positive integers.
What is a + b ?
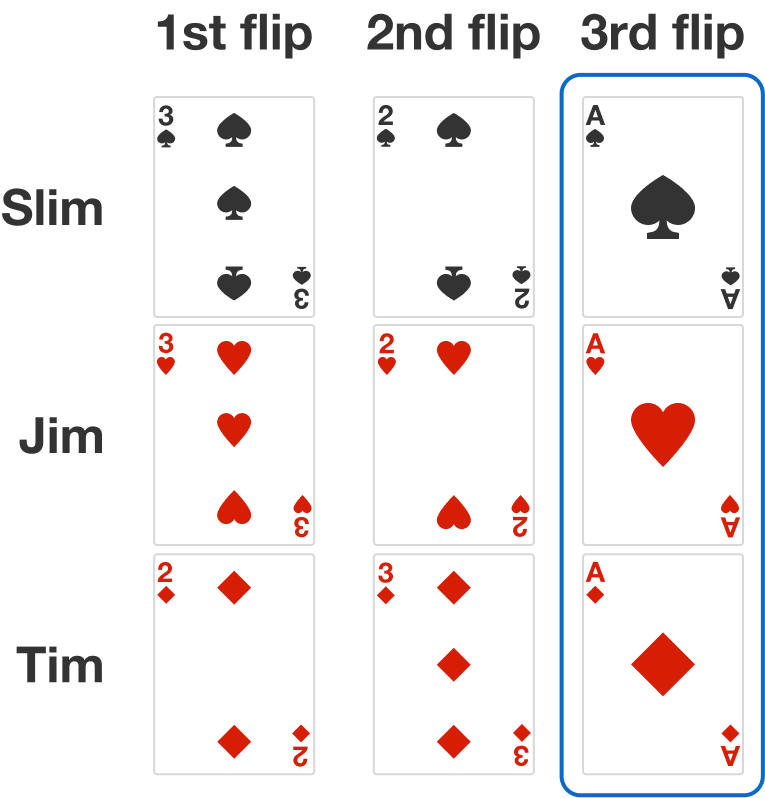 The three-way match can be on any of the flips, and can be on more than one flip. In this example, there is a three-way match on the third flip.
The three-way match can be on any of the flips, and can be on more than one flip. In this example, there is a three-way match on the third flip.
The answer is 23.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Thanks for the problem! Even with 3 cards I really had to think it through carefully, (I got it on my second attempt). I actually just fixed Slim's sequence at A-2-3 and looked at the 3!*3! = 36 possibilities for how Jim and Tim laid down their cards, and then found the complement, i.e., how many ways there were no three-way matches and then subtracted that tally from 36, (for some reason I found that easier). Now on to the general case for n cards......
Log in to reply
Yup... I was quite surprised that even the n = 3 case was non-trivial. Would love to find an elegant solution for n cards!
Possibly recursion?
Log in to reply
Yes, I think recursion is part of the method. For n = 4 I'm getting
P 3 ( 4 , 0 ) = 5 7 6 4 5 3 = 1 9 2 1 5 1 ≈ 0 . 7 8 6 5 , P 3 ( 4 , 1 ) = 5 7 6 1 0 4 = 7 2 1 3 ≈ 0 . 1 8 0 6 , P 3 ( 4 , 2 ) = 5 7 6 1 8 = 3 2 1 = 0 . 0 3 1 2 5 and P 3 ( 4 , 4 ) = 5 7 6 1 ≈ 0 . 0 0 1 7 4 .
I find that, for example, P 3 ( n , m ) = ( m ! ) 2 × ( m n ) P 3 ( n − m , 0 ) for m = 1 , 2 , . . . , n − 2 . (Clearly P 3 ( n , n ) = ( n ! ) 2 1 for all n ≥ 1 .)
In a similar way, once we establish the P 3 ( n , 0 ) 's, we can quickly calculate the other P 3 ( n , m ) 's, but a general formula for P 3 ( n , 0 ) is elusive.
Edit: Aha! The P 3 ( n , 0 ) 's are based on coincidence-free 2-tuples of length n . So I'm getting P 3 ( 7 , 1 ) ≈ 0 . 1 2 1 , from P 3 ( 6 , 0 ) ≈ 0 . 8 6 8 3 .
Other OEIS entries can deal with the P k ( n , 0 ) 's for k > 3 . From small acorns grow mighty oaks. :)
Log in to reply
@Brian Charlesworth – Whoa.. So if I read this correctly then, this could give us a mechanism for calculating all P k ( m , n ) ?
Log in to reply
@Geoff Pilling – Yup, I think so, at least for k = 3 , 4 , 5 , 6 , 7 , (which were the only OEIS sequences I could find). Once we have the P k ( n , 0 ) 's we can get the rest. I'm not sure how it was derived yet, but the link provides the recursive formula
P 3 ( n , 0 ) = n 2 P 3 ( n − 1 , 0 ) + n ( n − 1 ) P 3 ( n − 2 , 0 ) + ( − 1 ) n .
Apparently we've tumbled into the realm of topological coincidence theory. :)
@Brian Charlesworth – Hmm, I don't follow... How is P k ( n , m ) defined?
Inclusion Exclusion principle is your friend.
Actually, interestingly, calculating the expected number of matches is much easier. Here is a problem for your edification :)
I tried that too, but I am missing something. My count of how many ways there is to avoid any three-way matches isn't that much... the permutations I calculated are:
3 * 2 * 1 ways for Slim, 3 * 2 * 1 for Jim, then 2 * 1 * 1 for Tim
For example: A B C -> 6 ways to arrange A B C -> 6 ways to arrange B C A -> only 2 ways, 2 for the first card, then only 1 possible way to arrange the last 2 to avoid the match...
What am I missing?
How are 5 and 18 coprimes???
Log in to reply
Two positive integers are coprime if their greatest common divisor is 1. This is the case for 5 and 1 8 = 2 × 3 2 .
Counterintuitive probabilities like this are always fun to work out just because they're so surprisingly likely. I mean, your odds are a percentage between 1/4 and 1/3.
Log in to reply
I must not be reading the problem the same way. If each person turns up a card with three possibilities, then there are 27 ways the cards can come up, of which 3 match. Thus the probability of a non-match on any turn is 8/9. The probability of a non-match in three turns is (8/9)^3 = 512/729. Therefore, the probability of at least one match in three turns is 1 - 512/729 = 217/729. I also ran a simulation, three guys flipping a card valued 1, 2, or 3, and counting the number of times we got at least one match. My proportion of success matched my prediction to the third decimal place (over 1M trials).
Log in to reply
Did you see Binky's solution?
"The probability of a non-match in three turns is (8/9)^3 = 512/729."
No. The three flips are not independent, after someone has flipped (say) a 2 on round one, only the ace and three are available for the next flip, and the third flip is determined by the second. Your solution would work if they were rolling a die and outputting the value mod 3, but here we are talking about cards without replacement.
The problem was not stated clearly. It does not say they have to use up all 3 of their cards. I was assuming they were randomly using 1 of the 3 cards on each try. On each try, there are 3 out of 27 ways they could match or 1/3. If you repeat this experiment 3 times, the probability of at least once is 1 - (1 - 1/3)^3 = 19/27. 19+27=46. It should have said "they simultaneously flip over one of their remaining cards".
I have trouble with choosing the remaining cards. 2! 2! 2! I think. what i missed?
Log in to reply
You are correct that after the first flip their are 8 ways the remaining cards can be flipped.
Regardless of the order of Slim's cards, the probability of the other cards matching Slim's is the same. (Consider, even if Slim's cards are not in order A 2 3 , we can change the flip order so this is the case, and the number of matches will be the same).
There are 6 ways of ordering 3 cards. This means there are 6 × 6 = 3 6 ways of ordering Jim & Tim's cards in relation to Slim's cards.
If there is exactly 1 matching flip, there are 3 possible ways to order the remaining 4 cards without resulting in more matches. as there are 3 flips, the total number of permutations of exactly 1 matching flip is 3 × 3 = 9 .
There cannot be exactly 2 matching flips. If 2 flips are matching, the remaining cards are all the same.
There is only 1 way of having 3 matching flips.
This gives us a total of 1 0 permutations with at least one matching flip, out of a total 3 6 permutations. As such, the probability of this happening is 3 6 1 0 which cancels down to 1 8 5 , giving us our answer of 5 + 1 8 = 2 3 .
WLOG*, Slim turns over ( 1 , 2 , 3 ) in order. There are 3 cases based on what Tim turns over
-
With probability 1 / 6 , Tim also turns over ( 1 , 2 , 3 ) in that order. In this case Jim matches at least one of the three with probability 2 / 3 .
-
With probability 1 / 2 , Tim matches exactly one of the three cards: ( 1 , 3 , 2 ) or ( 3 , 2 , 1 ) or ( 2 , 1 , 3 ) . In this case Jim matches the same card with probability 1 / 3 .
-
With probability 1 / 3 , Tim doesn't match any of the three: ( 2 , 3 , 1 ) or ( 3 , 1 , 2 ) . In this case no match is possible.
Thus the probability of at least one match is ( 1 / 6 ) ∗ ( 2 / 3 ) + ( 1 / 2 ) ∗ ( 1 / 3 ) + ( 1 / 3 ) ∗ 0 = 5 / 1 8 . Thus a = 5 and b = 1 8 and a + b = 2 3 .
*WLOG = Without loss of generality
what is this WLOG. can you elaborate on this.
The permutation group S3 contains six elements: in cycle notation, (), (A2),(23),(A3),(A23) & (A32). So there is one cycle of length 0 (the identity), three cycles of length 2 & two cycles of length 3.
There is a 13/18 probability that there is no three-way match: we can show this using a probability tree with three branches, and only a depth of two.
We can let Slim’s cards come up in any order.
I) Jim’s cards have a 1/6 probability of turning up the same as Slim’s, with the identity permutation (). Then the permutation to Tim’s cards, for all of his to be different, would have to be a cycle of length three, (A23) or (A32), adding up to a 1/3 probability. So the joint probability of no match with this starting case would be 6 1 * 3 1 = 1 8 1 .
II) Jim’s cards have a 1/2 probability of turning up one the same and two different from Slim’s, with the length-two cycles (A2),(23) or (A3). At the turn where the two previous players’ cards were the same, Tim’s card would have to be different (the other turns don’t matter), and that would happen with a 3 2 probability. So the joint probability of no match with this starting case would be 2 1 * 3 2 = 3 1 .
III) Jim’s cards have a 1/3 probability of turning up all different from Slim’s—with the length-three cycles (A23) or (A32)—in which case Tim’s cards could come up in any order and there would be no three-way match. So the probability of a match not happening this way is 3 1 * 1, so also 3 1 .
The total probability of a three-way match not happening, since the three cases above are independent, is 3 1 + 3 1 + 1 8 1 = 1 8 1 3 . So the probability of the match happening is 1 8 5 , and the answer, 5+18, is 2 3 .
There are three possible cases for the first flip:
• Jim's and Tim's card will both match Slim's, with a 9 1 probability. This is a 3-way match already. It doesn't matter what happens on the subsequent flips.
• Jim's and Tim's card will both be different from Slim's, with a 9 2 probability. This leaves zero probability of a 3-way match on either of the subsequent flips.
• Exactly two of the three cards match. The possibility of this is the residual 1 – 9 1 – 9 2 = 3 2 .
In the third case, the players hold two cards each, and within those three pairs there is only one matching set. There are 2 x 2 x 2 = 8 possible plays, and 2 of those include a 3-way match (on the second flip, or on the third flip). So, given the third case for the first flip, the chance of a subsequent 3-way flip is 8 2 = 4 1 .
Therefore the total probability of getting a 3-way match is the sum of this happening by the first case or the third case:
9 1 + 3 2 • 4 1 = 9 1 + 6 1 = 1 8 2 + 1 8 3 = 1 8 5 .
The answer is therefore 5 + 18 = 23.
There are 2 possibilities. Either you get a match on all three turns, or on only one of them.
If its all three, then there are six ways to do it. 3 permutations on the order of Ace, two and three.
If its just one then there are 54 ways to do it:
3 ⋅ 3 ⋅ 6 + 6 = 6 0 ways
And there are 6 3 = 2 1 6 ways the cards could be played. (Each player has 6 permutations for their 3 cards)
2 1 6 6 0 = 1 8 5
5 + 1 8 = 2 3