Three Orthogonal Circles
If three circles with radii r 1 , r 2 , and r 3 are placed so that each one is orthogonal to the other two, and the triangle formed by their centers has an area of A = r 1 r 2 r 3 , then:
r 1 2 1 + r 2 2 1 + r 3 2 1 = k
for a constant k . Find k .
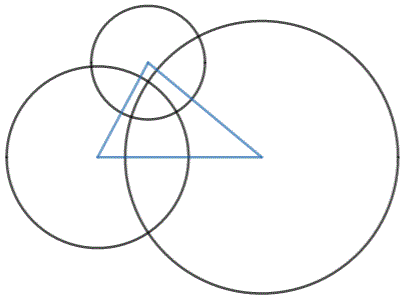
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Sorry, I did not understand your 2nd step. Nice solution by the way. I started with the same approach but was stuck at this step only. Using Heron's formula was tedious
Log in to reply
I used Heron's formula for that step. There are different versions of Heron's formula you can use to made it less tedious, like A = 4 1 ( a 2 + b 2 + c 2 ) 2 − 2 ( a 4 + b 4 + c 4 ) (instead of the traditional A = s ( s − a ) ( s − b ) ( s − c ) ).
Log in to reply
So that means:
r 1 r 2 r 3 = 4 1 ( ( r 1 2 + r 2 2 ) + ( r 2 2 + r 3 2 ) + ( r 3 2 + r 1 2 ) ) 2 − 2 ( ( r 1 2 + r 2 2 ) 2 + ( r 2 2 + r 3 2 ) 2 + ( r 3 2 + r 1 2 ) 2 )
On circles with radii r 1 and r 2 , the following red triangle can be drawn, which shares a side with the original blue triangle:
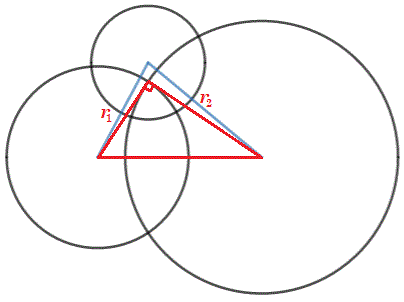
Since one vertex of the red triangle is at the intersection of the two orthogonal circles, it is a right triangle, and since two of the legs are the radii r 1 and r 2 , by the Pythagorean Theorem the hypotenuse (and the side of the original blue triangle) is a = r 1 2 + r 2 2 .
By a similar argument, b = r 1 2 + r 3 2 and c = r 2 2 + r 3 2 .
By a version of Heron's formula, the area of the original blue triangle is A = 4 1 ( a 2 + b 2 + c 2 ) 2 − 2 ( a 4 + b 4 + c 4 ) , which after substituting a = r 1 2 + r 2 2 , b = r 1 2 + r 3 2 , and c = r 2 2 + r 3 2 , becomes A = 4 1 ( ( r 1 2 + r 2 2 ) + ( r 1 2 + r 3 2 ) + ( r 2 2 + r 3 2 ) ) 2 − 2 ( ( r 1 2 + r 2 2 ) 2 + ( r 1 2 + r 3 2 ) 2 + ( r 2 2 + r 3 2 ) 2 ) , and simplifies to A = 2 1 r 1 2 r 2 2 + r 1 2 r 3 2 + r 2 2 r 3 2
We are also given that A = r 1 r 2 r 3 , so A = r 1 r 2 r 3 = 2 1 r 1 2 r 2 2 + r 1 2 r 3 2 + r 2 2 r 3 2 , which can be rearranged to:
r 1 2 1 + r 2 2 1 + r 3 2 1 = 4
Therefore, k = 4 .
Let us call the distance between the centres of the circles of radii r 1 and r 2 as r 1 2 , and similarly the other two distances as r 2 3 and r 3 1 . Then
r 1 2 = r 1 2 + r 2 2 , r 2 3 = r 2 2 + r 3 2 , r 3 1 = r 3 2 + r 1 2 .
Then r 1 r 2 r 3 = 4 r 1 2 r 2 2 + r 2 2 r 3 2 + r 3 2 r 1 2
Implies r 1 2 1 + r 2 2 1 + r 3 2 1 = 4 .