Three Pentagons Cover a Fourth
In this diagram, three regular pentagons (red, blue, green) of side length 1 overlap to completely cover a fourth regular pentagon (black) of side length s .
What's the largest possible value of s ?
Give your answer as ⌊ 1 0 0 0 s ⌋ .
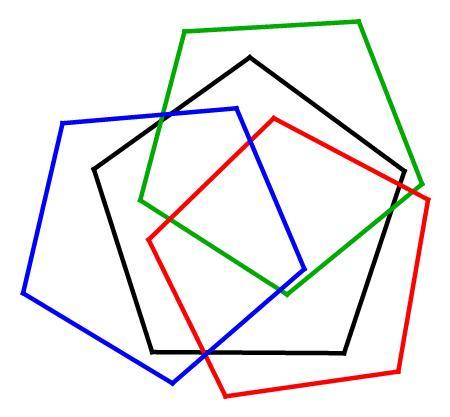
Note: You can rotate or place the pentagons however you want.
The answer is 1264.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
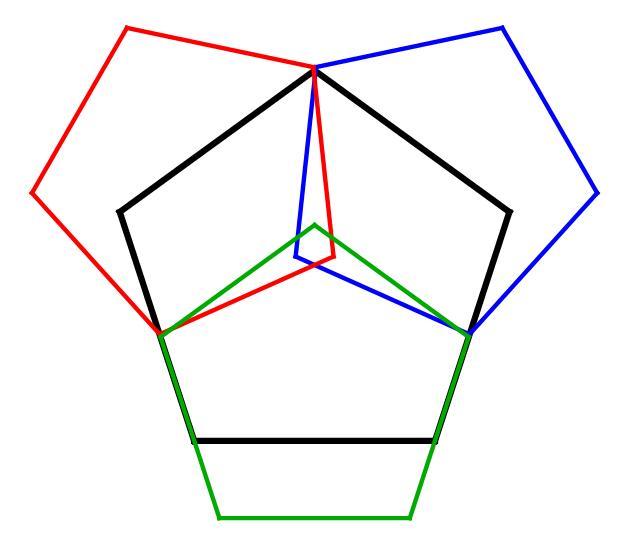
Actually, your solution looks to be correct, as simple as it is. Let me try to post a more accurate figure.
Log in to reply
What do you mean with 'misproportioned'? It's a precise GeoGebra construction.
And any comments on optimality? Is there maybe an even better solution?
I just don't want anyone else to look for a better solution (for 2 hours), even though he tried to enter the optimal one.
Log in to reply
Well I don't know what's going on with our figures. I'm using a ruler to measure the sides as they appear on the computer screen, and yours is just a bit off. I don't doubt that you've used something like GeoGebra to construct yours, but this is not a basis for arguing about whether or not your solution is valid.
Yeah, definitely the base of the green pentagon measures a bit short. Why that is, I have no idea.
As for optimality, well, we'll find out if anyone else can do better.
Log in to reply
@Michael Mendrin – We don't argue about the validity of my solution, my derivation shows that the solution is valid. Actually we argue about the validity of my figure; I would say that a precise GeoGebra construction speaks more for a precise figure than you checking it with a ruler speaks against it. The lines are very thick, that's probably why you fail with the ruler. (For me it's roughly correct with the ruler)
Ok, I'm not sure how the whole 'Problems of the week' system works, but I think that the 'correct solution' should never be wrong, otherwise people waste their time finding the correct 'correct solution', even though they have it already.
Log in to reply
@Yannick Ruffiner – I've already posted in "View Reports", so that Brilliant Staff can review the matter and get this resolved. As for "measuring with a ruler", I've been a draftsman for a lot of my earlier years. But, again, this is not any basis for any argument about your solution. We're not in dispute about that.
This is symmetrical.Symmetry is cruicial in some optimisation problem. There is symmetry in the problem. We expect the solution to be symmetrical. Just like maximum value of a+b+c given abc=constant. Here there is a symmetry. We know that maximum is attained.but how do you show that this gives the maximum s. I thought in this way but was not confident it will work.
I think if we solve the following problem we are done. Suppose we have two pentagons of side length 1 which are intersecting. How do you draw another pentagon of side length 1 such it encloses of pentagon of side s. How do you draw this pentagon so that s assumes the maximum possible value. If we have this in hand. We can focus on how to draw two interesting pentagons of side length 1. So that s assumes the maximum possible value.
Can we generalise this result to polygons with n sides.
Note: See Yannick Ruffiner's solution
For this lesser solution, refer to graphic at bottom for details
s
1
=
2
1
(
1
+
5
)
s
2
=
2
1
s
4
+
5
s
3
=
2
1
4
−
(
5
+
5
)
s
+
(
5
+
2
5
)
s
2
θ
1
=
5
3
π
−
A
r
c
S
i
n
(
s
2
s
1
S
i
n
(
5
2
π
)
)
θ
2
=
A
r
c
S
i
n
(
s
3
s
−
1
S
i
n
(
5
3
π
−
A
r
c
S
i
n
(
2
s
2
s
S
i
n
(
5
3
π
)
)
)
)
θ
3
=
5
2
π
−
A
r
c
S
i
n
(
s
3
1
S
i
n
(
5
3
π
)
)
Find by numerical means s such that
θ 1 + θ 2 + θ 3 = 5 2 π
which works out to s = 1 . 2 5 2 1 9 0 7 1 3 8 9 5 2 8 2 2 4 . . . .
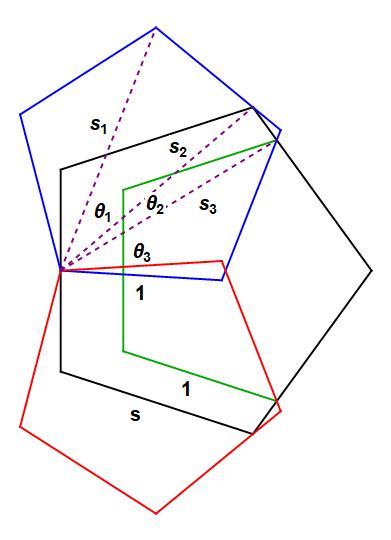
This is the configuration I found and got the same number with GSP. I focussed on the little triangle at the ends of s1 and s2 so if I get around to a solution it will look different.
I don't see how there could be a better configuration.
Log in to reply
Yes, that is the key, that real tiny triangle at the corner of the blue pentagon. It's just a question of finding the most convenient way to even approximate s , where the base of that triangle is s − 1 . No explicit expression for s seems possible. I thought this problem would be easier than this.
can you explain me why this configuration works?
I think I found a better solution, correct me if you find a mistake. How did you proof that your solution gives the largest s ?
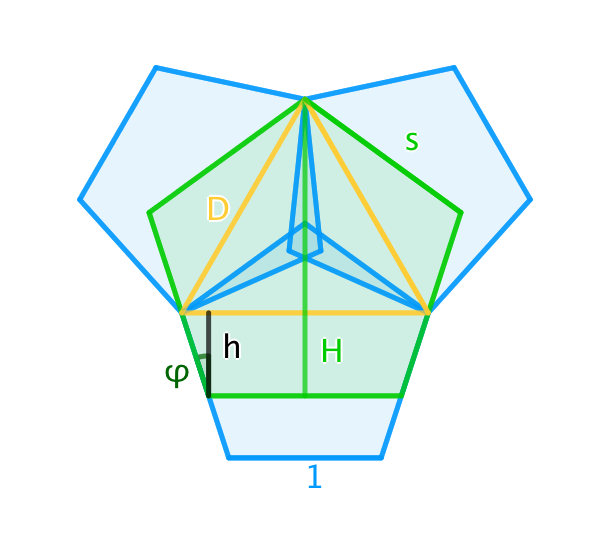
First D , H and φ can be described easily with basic pentagon geometry:
φ = 1 0 8 ∘ − 9 0 ∘ = 1 8 ∘ D = 2 1 ( 1 + 5 ) H = s ⋅ 2 1 5 + 2 ∗ 5
Now I describe the base of the yellow triangle and the height of the green pentagon in a different way:
D = s + 2 ⋅ h tan φ H = h + 2 3 ⋅ D
This gives a system of two equations and two unknowns h , s which solves to s = 1 . 2 6 4 3 1 3 . . .