'Tic-tac-toe' or 'cross & noughts'
 Two amateur people are playing a game of tic-tac-toe. Each person places his/her mark, either
or
. We do not know who started first.
Two amateur people are playing a game of tic-tac-toe. Each person places his/her mark, either
or
. We do not know who started first.
After the first player has placed his/her second mark, the players will always place his or her mark in a line that already contains
(a)
two of his/her own marks,
(b)
two of his/her opponent's marks,
(c)
giving priority to (a) over (b).
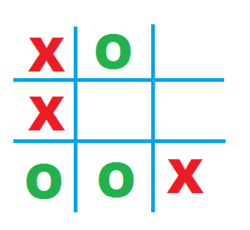
Only the last mark to be placed in the game shown in the figure has not been given. Who will win the game, or
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the no. in each block represent the location of a mark. Then, from rule 3, the seventh mark must be placed in block 5. And from rule 2, the seventh mark wins for both X and O.
Since lines 1-4-7 and 7-8-9 have 2 opponent marks, this tells us that the 6th mark must either be in block 7 or block 9. However, placing the 6th mark in block 7 would contradict rule 3c, where O would rather play it in block 5 and win the game. Thus, the sixth mark was placed in block 9 and it was 'X'.
Accordingly, the 7th or the final mark must be 'O' and O wins the game.