Tic Tac Toe Twist
In this example, Xavier begins by placing 2 Xs along a diagonal. Then, Olivia plays two Os along the right column.
Xavier and Olivia play a variation of tic-tac-toe on a 4 × 4 board in which they alternate placing 2 letters on each turn. The first player to get 4 of their letters in a horizontal, vertical, or diagonal row is the winner.
If Xavier goes first and both players play optimally, who will win?
Note : The image is an example of play, and does not necessarily represent optimal play for either player.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
If I go first and place 2 X in the center of one diagonal, then my opponent is forced to take the 2 corners of that diagonal (although I would win). After that I take the rest of the center of the grid and no matter which is the next move of my opponent I will have always a way to win in my next move...
Log in to reply
No sorry... it is clear in the image of the problem that I'm wrong XDXD
I thought the exact same thing...
please help me: from the example picture, X can win by setting in the top right corner and diagonally below/left. this creates threats in the 3rd column, the 2nd row and the diagonal. How should O have her first turn to avoid this?
Log in to reply
O goes in the top two corners.
O's first round moves in the example are suboptimal: the proper move is to take one of the required corners, then place the second O in one of the inside spaces, next to both X spots.
Log in to reply
So much confusion could be avoided, by saying that you start with a fresh board, not continuing what the picture states
I agree with you. X can win
I'm so confused by this problem. If X puts it's first two X's right next to each other(not diagonal) in the center then O has to put atleast one in that row/column to stop it. Due to symmetry I'll just go with the second row looking like: [o][x][x][-]. Now, no matter where O places it's second move, there is always a way that X can force a win by putting two X's in the top or bottom row, creating 3 threats: 1 row, 1 column and 1 diagonal(and if played optimally neither of which share boxes so there is no way for O to block them all). Is there really something that I'm overlooking right now or is the answer to this problem actually wrong?
Log in to reply
But O can use its first O to block the threat and place its second in the corner of the same column creating its own threat and distracting X from following your strategy. This leads to a draw.
Log in to reply
The thing is, if I'm not mistaken, it actually can't. Consider O places it's O in the top left corner with the second row still being [o][x][x][-] then X can just put one X in the bottom left corner(blocking O and creating 1 threat) and the second one in the same row on column 3(creating 2 more threats). If instead O chooses the bottom corner we just put X in the first two columns in row 1. Either way, X creates 3 threats and wins.
Log in to reply
@Dennis Kindervater – Why is O putting their move in the top left corner?
X in second row, third column can be followed by O in second row, fourth column. This threatens a win for O so X must respond in first row, fourth column.
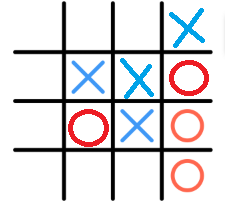
X doesn't have a win here. It looks like maybe you're thinking it's a win with 3 in a row? That's not how the rules are given.
Log in to reply
@Jason Dyer – Ah thanks, now I figured out where I went wrong =) . It wasn't that I thought 3 in a row wins. I missed that O can block 2 threats with one move in its 2nd turn when it puts its second move on its 1st turn in one of the 2 open center spots.
While I don't think the result is wrong, the Given answer seems to over-emphasize playing the corner on O's first turn. I'm not sure what exactly is required, but simply playing "block, then play any corner" is not enough.
 Example 1
Example 1
First we have X playing a Diagonal move in the inner spaces. This picture shows the 7 possible responses by O (before symmetries) and the corresponding moves by X that would guarantee a win in 6 of those moves. The only way O avoids the loss is to block both Diagonals with a corner and an inside space.
 Example 2
Example 2
Next we have X playing a row (or column, with rotation) in the inner spaces. Again, all the possible responses by O and the moves that guarantee X the win. Notably, all four "block, then claim a corner" responses can be beaten.
It seems like the correct moves in both cases involve blocking as many potential threats as possible (each X has one remaining potential threat it can be used for) in a way that makes it hard to create new threats. In all three cases above, X can play the common space that turns both potential threats into actual threats but then they can't use the remaining move to make a third threat, or they can leave the common space open and use the Xs in other places to activate both potential threats while generating a third threat,but then O can use the common space to block 2 threats in one move, and the remaining move to block the third threat.
Log in to reply
As far as I can tell, your reply contains the only proper responses to opening with both Xs in the center. And you show why other moves do not work.
Very clear and helpful.
I'm not sure how to play if X varies from this opening, but it certainly makes for an entertaining variant on Tic-Tac-Toe! I hope to get my kids and/or some friends interested in this, so I don't want to study it too much too soon.
Log in to reply
Very well done. It certainly looks like X can force a win by playing properly, as O looks to be in a really bad state after X's second turn. But your answer explains that O can escape by marking the common space, then deal with the remaining threat.
I disagree. I think that with the first option below X wins. It creates 3 simultaneous threats. No way O can avoid X win.
Log in to reply
well. If the example is not a real play, since Olivia will never play this option, then the answer will be an always draw.
Log in to reply
If the players always play optimally, why they give an example that is not the case?
I am surprised by the comment "The only way to end a turn creating 3 threats is to take a corner" The centre squares and the corners are of exactly equal value. Both have 3 possible winning lines going through them. The edge squares only have 2 possible winning lines going through them.
Log in to reply
The first 2 moves of O (assuming that X plays optimally by taking corners or centres) is to play symmetrically. He has then already blocked 6 of the 10 winning rows.
Log in to reply
That has been demonstrated to be incorrect. One O must be placed to block the threatened win, and the other must be placed so as to prevent X from threatening 3 (or more) ways to win on his next turn.
See the excellent reply by David Lamoureux.
It’s not clear whether the two marks must be adjacent?
I disagree. X wins by playing top left and bottom left. The first placing of O is forced and there are 13 possible second placings. All lead to a win for X (since there are at least 3 options for forming four in a row in each case). XO.X X.OX X..O X..X X... X... X..X X..X X..X X..X X..X X..X X.X. O... O... O... OO.X O.OX O.XO O... O... O... O... O... O... O.X. .... .... ..X. .... .... .... O... .O.. ..O. ...O .... .... .... X..X X..X X.X. X... X..X X..X X..X X..X X..X X..X XO.X X.OX X..O
Xavier wins on his next move. Numbering the squares from left to right and starting with the top row, Xavier puts an X in cell 4 and cell 7 to win. On his next move, he can win with 4,7,10,13 by move 10,13 or 3,7,11,15 by move 3,15 or 5,6,7,8 by move 5,8. Since the wins are a diagonal, column and row, Olivia would need 3 moves to block but she only has 2 moves so she loses and Xavier wins on the next move.
Log in to reply
The image says the moves shown are an example of play. Olivia did not play optimally.
Perhaps im missing something, as I admit Im writing this semi-impulsive. But, if Xavier went next (in the example) & occupied all four center squares he most certainly have the advantage to win. No?
Log in to reply
No because Olivia is threatening to win on her very next turn.
In the example given Xavier can win, but must be careful to block Olivia as part of his next turn.
Of course, Olivia has not played optimally, which is why Xavier can force the win in the example. If she (and he) does play optimally, it would be a draw.
I disagree. Assuming that columns are labeled as A, B, C, D and rows 1..4 player1 occupies B2 and C2 threatening row 2. Player2 blacks row2 in D2 (or A1). Now player2 has his last move: either it occupies one of the 2 corners of column D or one of column A. Column A poses no threat so player1 can occupy all center cases and win. If player2 occupies one of the two corners of column D player1 can still win by moving into the remaining corner on column D (blocking the threat) e.g. D4 and in B4, hence gaining the triple threat on: row4, diagonal A1-D4 and column B. Player1 wins.
Log in to reply
That's probably player1's best opening, but it can be blocked by player2 making their second play the non-adjacent corner. Player1's triple threat can then be blocked by player2 in the square where the diagonal threat crosses the column threat.
Actually, this question I suppose there is a missing point that: "Are they attempt to win?" or any "wrong answer" (like they draw a different answer from their thinking. In that case, the answer should be "depend". Besides, the image above is just an 'example', if the question would be more clearly as above and exactly like the picture above, the answer would be Xavier (I haven't checked yet). I have found 2 examples that are "draw" 1: Player 1 (X): A1 - A2; Player 2 (O): A3 - B1; Player 1 (X): B2 - C3; Player 2 (O): D2 - D4 and so on. Or the worst scenario for player 1. 2. Player 1 (X): A1 - A2; Player 2 (O): A4 - B1; Player 1 (X): B2 - C2; Player 2 (O): D2 - C3.
=> The core of being draw that 1 player must have their markings (X or O) in any horizontal or vertical lines without having the same markings on the place such as the "letter" - "number" (D4, for example). Like if you want to draw, your marking, O, for example should be B1 - D2 - C3 - A4 (no letters and numbers is repeated), except 2 scenarios that A1 - B2 - C3 - D4, and A4 - B3 - C2 - D1.
The problem statement should say that Xaview plays "X" and Oliver plays "O". It can be inferred, but it is not necessarily so.
SO I just thought, what if Xavier doesn't notice Olivia could win. Unless he's a robot all humans are prone to mistakes, and he could miss that. Think about it: How many times in games similar to tic-tac-toe do you fail to notice when the other person is about to win because your so focused on offense you forget about difference.
Besides that I agree with this answer that it would be a draw. In the example, Xavier begins by placing 2 Xs along a diagonal. Then, Olivia plays two Os along the right column. By now it's Xavier's turn. He can place a X in the upper far right corner to prevent Olivia from winning, but then after that it's just impossible to win because each would be worried about each the other person winning that they use one X or O to block the other person that it only leaves the player one marking to place in their row or column to ensure their personal triumph. Then the other player will most likely block the other player, repeating this process until it's a tie.
In the example given in the problem statement, Olivia has played poorly and Xavier can force a win. He does this by playing in the top right corner (to block), then in the top right middle creating a triple threat. Olivia should have blocked, then played in the middle to prevent any triple threat.
The game is deeper than it looks like at first, but is a draw if each player plays optimally.
- 2X are put in the diagonally opposite corners.
2O in btw them.
2X in other two diagonally opposite corners.
Now Xavier has 4 winning lines.
Log in to reply
Your step 2. is not optimal. O should use one move to block in between, the other to take a vacant corner.
Please see David Vreken's posted solution.
X..xoxooxxoxxxx.XOXXOOXOXXX.XXXXX.XXXXOX...
Or this: 2x 2o
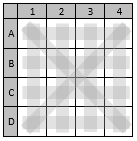
The board has only 10 possible winning lines: 4 horizontal, 4 vertical, and 2 diagonal, as shown below:
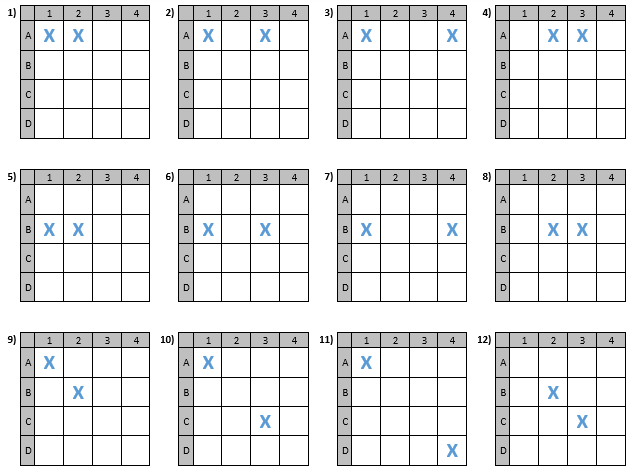
If Xavier is playing optimally, his first turn will be to place 2 X's along 1 of the 10 possible winning lines, so that Olivia must waste an O on her first turn to block it. After rotations and reflections, this can be done in 12 different ways:
Now on Olivia's first turn, she must use up one O to block Xavier's first possible winning line, and use her second O to block Xavier from getting a "triple threat" (at least 2 X's in at least 3 different unblocked possible winning lines) because she can only block 2 out of the 3 possible winning lines on her second turn, and then Xavier will win by completing the third possible winning line on his third turn. To prevent this from happening, the following diagram shows 1 possible way for Olivia to counter each of the 12 different ways that Xavier can start the game (the blue shaded lines represent unblocked possible winning lines still available to Xavier after Olivia's first turn):
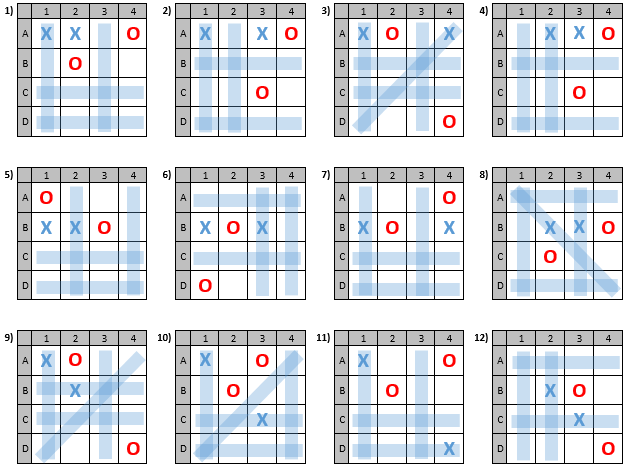
For all scenarios except for 3, 8, 9, and 10, Xavier is left with 4 unblocked possible winning lines, 1 with 1 X and 3 with no X's, which makes it impossible for Xavier to play a "triple threat". His optimal play then is to make a "double threat" (at least 2 X's in at least 2 different unblocked possible winning lines), but Olivia can block both of those on her next turn, leaving at most 2 unblocked possible winning lines, which Olivia can then block on her last turn. For example, in Scenario 1, Xavier can place X's at D1 and D3 to make a "double threat" with the first column and last row, Olivia can block them by placing O's at C1 and D2, Xavier places 2 X's in his only remaining unblocked possible winning line at say C3 and B3, and Olivia places an O at A3 on her last turn, resulting in a draw.
For scenarios 3, 8, 9, and 10, Xavier is left with 5 unblocked possible winning lines, 2 with 1 X each and 3 with no X's. Now Xavier can play a "triple threat", but Olivia can block it with just 2 O's because 2 out of the 3 threats must always intersect at one point. For example, in Scenario 3, Xavier can place X's at B1 and B3 to make threats on the first column, second row, and one of the diagonals, but Olivia can block all three threats by placing her O's at D1 and B2. After this there is once again only 2 unblocked possible winning lines, which Olivia can block on her last turn, resulting in a draw.
Therefore, if both players play optimally, the game will end in a draw.
that was easy, thanks to all of y'all'
While this is not a proof of the answer , it does hint at the correct answer:
- A 1x1 Tic-Tac-Toe is by definition won by the person that starts.
- A 2x2 Tic-Tac-Toe is inevitably won by the person that starts.
- A 3x3 Tic-Tac-Toe is drawn with optimal play.
Given that sequence, it is logical to infer that it gets harder to win for the starter the larger the grid. Otherwise 3x3 must be a special case. However, starting is almost certainly advantageous (you have at least as many squares as the opponent and you get to choose both before and after them,) so it should tend toward a draw rather than a loss.
This only holds for one tile at a time play, two tiles at once is guaranteed win for 1x1, 2x2 and 3x3 for the person who goes first.
3x3 Tic-Tac-Toe has optimal strategies that will always win if you are the first player.
Log in to reply
does this include when the opponent plays optimally too?
Not possible if both players play optimally
Not if both play optimally
Remember that in this question, you get to place two symbols on each turn. For 3x3 tic-tac-toe, numbering the fields as on a telephone/pin-pad or computer keyboard (they are rotations of eachother), the first player will play 1 and 6, giving five possible lines to win on. The second player can block four out of five of these at best.
Without necessarily going into details, a 4x4 tic-tac-toe gives both players absolute control over the board, simply because they have 4 pieces to move equally, thus there's always a move left to counter that of the opponent, denying them victory. Thus the only way to win is for the opponent to pass a turn or consciously grant it. *An evenly matched game doesn't matter who comes first! *
Zavisr plays 2 noughts and wins
What about chess? Same Initial conditions described by you yet still not shown to be a draw always.
Log in to reply
That's because we haven't figured out a way to play perfectly optimal chess - not even with computers.
This does not fully address the problem at all.
@James Liu has given a very bright answer. in chess the possible moves are very large that we really can't play perfectly to counter each move, else we should end up with a draw.
First lets note that the first player will always be on the "offensive", and the second on the "defensive". It is simply because the players play optimally. Whatever position the 2nd player achieves, the first could achieve it first. Then the second player plays to block the game. It is done once one of its letters is placed in every vertical row, horizontal row and great diagonal. For a nxn tic tac toe (n>3), it can be done in n moves without considering the first player moves (remember the extended 8 queens prob). During this time the first player can only complete one row. For a second, it will need at least n-1 moves since rows have at most 1 square in common. So in n+1 moves, it can only do 1 threat that will force a play from 2nd player. Then in n+1 moves, 2nd player will always block the game. And if it can do it, 1st player can too.
The only way to prove that this game "is a draw" is to use a computer to analyse how black draws with any first 2 placements by white. The game is very finite; only a few hundreds possibility. Using symmetry it could easily be done by hands as for regular tic-tac-tow. Philosophical argument like: W attacks and B stops it, is ridiculous. B as to stop it and make it impossible for W to reply and ends-up with 3 threats.
Arsenio is correct X wins in the example provided
In the example given, if Xavier's next move is the upper right center and upper right corner, he has set up three ways to win that can't be blocked. While the example "does not necessarily represent optimal play for either player," it doesn't mean that it isn't. Try giving an example of optimal play, not this.
You are correct Ralh. So easy to see the triple threat. Was the author David purposely setting up a trick question by showing a bad example of Olivia's first turn ? Seems he should not have presented the pictured example if he didn't want us to proceedo from there.
I believe that there is an error in the question or my understanding of the question is flawed. If there is to be an X placed on the two opposite corners in the first turn then there is a scenario whereby if played in the best interest of the person who went first is a guaranteed win.
The only way to force a win is for a player to end his/her turn by creating 3 simultaneous threats since any two threats can be blocked. The only way to end a turn creating 3 threats is to take a corner, while having unhindered threats along the row, column and diagonal.* On your opponent’s first turn (regardless of whether he goes first or second) he will have at least one ‘free’ move (where he does not have to go for an immediate block). If he takes any corner with his first move, the triple threat strategy is blocked.