Tic Tic Tic

Logic Level 2

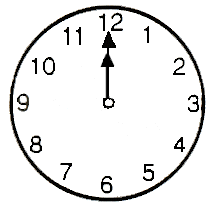
How many times in a day (24 hours) does the minutes hand and the seconds hand of the clock meet at the same point (as shown below)?

2048 1200 1440 3600 1416

1 solution

Ram Mohith
Jun 30, 2018

$\text{In one minute the minutes hand and the seconds hand of the clock meet for 1 time.}$

$\text{So, in 1 hour the minutes hand and the seconds hand of the clock meet for 60 times.}$

In, 1 day there are $24$ hours. So the minutes hand and the seconds hand meet for $24 \times 60 = 1440 ~ times$ .

$\text{Therefore, in 1 day the minutes hand and the seconds hand meet for }{\color{#20A900}1440}\text{ times.}$

In an hour,they meet 59 times,not 60.

X X - 2 years, 11 months ago

But how. In one hour there are 60 minutes therefore the meet 60 times

Ram Mohith - 2 years, 11 months ago

In an hour(let it be 1:00 to 2:00,but not including),the first time they meet is at 1:00.

The 2nd time they meet is at a time between 1:01 to 1:02.

The 3rd time they meet is at a time between 1:02 to 1:03.

The 4th time they meet is at a time between 1:03 to 1:04.

...

The 58th time they meet is at a time between 1:57 to 1:58.

The 59th time they meet is at a time between 1:58 to 1:59.

The 60th time they meet is exactly 2:00.

This "60th time" should be count as from 2:00 to 3:00,not 1:00 to 2:00.

So it should be 59 times.

X X - 2 years, 11 months ago

@X X – Will tue answer change now or will it remain same as 1440

Ram Mohith - 2 years, 11 months ago

@Ram Mohith – I think you can't change the answer.Maybe we should wait for a moderator.

X X - 2 years, 11 months ago

@X X – Other authors have been able to edit their challenged offerings. (It might have been only with the help of a moderator.

J B - 2 years, 10 months ago

@X X – It might have helped to do have first thought through this same exercise with the minute and hour hands: 2x11=22. It might also have helped to remember/realize that an analog clock is effectively a Vernier (dial) gauge of time (instead of distance). If you have actually counted the 9 tics on a decimal Vernier, it becomes obvious why n-1 is the true intersection count per clock cycle ; c/day=2, 12hr. : =24, 60min : c(n-1)=i; 2(12-1)=22, 24(60-1)=1416

J B - 2 years, 10 months ago

It should be 1416 times

Sonveer Yadav - 2 years, 9 months ago

I agree with Yadav.

Hosam Hajjir - 2 years, 3 months ago

Not all clocks have their hands run smoothly though :P . My clock has the minute hand moves only when the second hand reaches number 12. So if you take 0:0 at the start (don't count as "meet") then they meet at 1:1, 2:2, 3:3, ..., 59:59 and then both move to meet at 0:0 to start a new hour, making it 60 times.

Tbh, if the hands run smoothly, we wouldn't hear the sound 'tic tic tic' :D .

Phượng Mai Liên Hồng - 2 years, 2 months ago

Tic Tic Tic

1 solution

0 pending reports