Not-so-simple harmonic motion
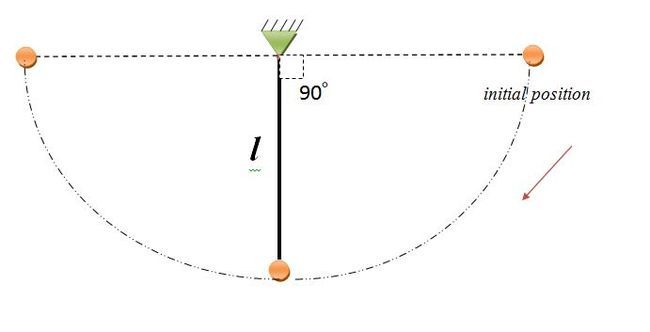 A pendulum has length
l
=
3
0
c
m
and a bob of mass
m
=
2
k
g
.
At time zero, the mass is brought
θ
=
9
0
°
from which it is released, with zero initial velocity.
A pendulum has length
l
=
3
0
c
m
and a bob of mass
m
=
2
k
g
.
At time zero, the mass is brought
θ
=
9
0
°
from which it is released, with zero initial velocity.
Find the time Δ t in seconds to reach the bob to the opposite end (left end).
Details
- g = 1 0 m / s 2 .
The answer is 0.64227.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Wow, that's about 15% off from what you'd get with the small angle approximation.
Log in to reply
Yup. The angle really does have to be small for the small angle approximation to be valid!
Log in to reply
i was right if i did't forget to write L , was i sir ? @Mark Hennings
How you wrote this- the first step? Is there any formula? :
T = 2 g ℓ ∫ − 2 1 π 2 1 π cos θ d θ
Log in to reply
see the report i wrote in reports section
I have a formula for θ ˙ 2 . Take the square root, and separate variables to solve this differential equation.
Log in to reply
But how you related T to your formula?
Log in to reply
@Priyanshu Mishra – T is the time ∫ d t that the pendulum takes to move from θ = − 2 1 π to 2 1 π .
Log in to reply
@Mark Hennings – That i know but please tell how you got relation between T and θ
Log in to reply
@Priyanshu Mishra – As I said, separate variables. We have d t d θ = θ ˙ 2 g ℓ cos θ d θ = ℓ 2 g cos θ = d t and now integrate.
Log in to reply
@Mark Hennings – Thanks.
By the way, do you know any website where i can draw physics diagrams and download it?
Who needs to solve elliptic integrals when you've got your very own personal computer? I feel like I have cheated...
The equation of motion for the pendulum is:
θ ¨ = − l g sin ( θ )
Here's a simulation I did using Runge-Kutta, and the results are strikingly accurate. The equation of motion is fed in, and is broken into two first order linked equations to apply the RK algorithm:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
|
As the angle through which the pendulum has been released is not small enough we cannot treat its motion as SHM.So now the usual way of circular motion works.obtain an integral.this can be evaluated by application of maclaurin series to the denominator.the correction in the period is to be noted.this is a form of elliptic integrals.
When the bob makes an angle θ with the downward vertical, conservation of energy tells us that 2 1 m ℓ 2 θ ˙ 2 + m g ℓ ( 1 − cos θ ) = m g ℓ and hence θ ˙ 2 = ℓ 2 g cos θ Alternatively, we could obtain this equation by considering the transverse equation of circular motion: m ℓ θ ¨ = − m g sin θ and integrating it once. Thus the time for the bob to sweep from one side to the other is T = = 2 g ℓ ∫ − 2 1 π 2 1 π cos θ d θ = g 2 ℓ ∫ 0 2 1 π cos θ d θ = g 2 ℓ ∫ 0 2 1 π ( 1 − sin 2 θ ) 4 3 cos θ d θ g 2 ℓ ∫ 0 1 ( 1 − x 2 ) 4 3 d x = 2 g ℓ ∫ 0 1 x 2 1 ( 1 − x ) 4 3 d x = 2 g ℓ B ( 2 1 , 4 1 ) which makes T = 0 . 6 4 2 2 7 .
This integral can also be evaluated in terms of elliptic integrals, but the beta function is probably more familiar!