Add 1 Or Multiply By 3
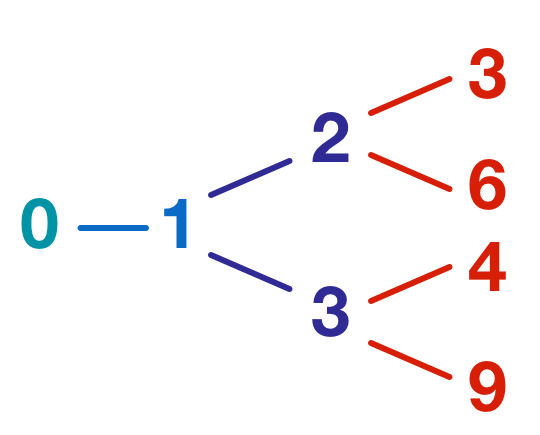
Consider the following game:
- You start with the number 0.
- Every move you can either add 1 or multiply by 3 . Lines in the above diagram represent possible moves.
What is the smallest number that takes at least 15 moves to make?
Clarification: You need to find the smallest number that can be made in 15 moves but can't be made with any fewer than 15 moves. e.g. 15 could be made in 15 moves (add 1, 15 times) but it can also be made in 5 moves: + 1 → × 3 → + 1 → + 1 → × 3 ,
So, 15 would not be a valid answer.
The answer is 404.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Sir, please elaborate your solution. I understand that you are using base 3 and that shifting thing too. But how can we know that it is the smallest. Plus how and where to implement shifts and addition. It's a very nice question.
Log in to reply
I've added a bit to my solution.
Make sense?
I'm a little worried that maybe my logic is flawed since no one seems to be getting the same answer that I did.
This would be a great time to see the answers people submitted to see if I was doing something very silly... :-/
Log in to reply
Sir, I guess I understood your concept here, the reason for using base 3 is that 3 = 1 0 3 and it can create shifts(absolutely brilliant). And sir, this is really a brilliant problem. Please post more problems like this.
Log in to reply
@Abhay Tiwari – Hey thanks, Abhay... Will do! (BTW I'm a big fan of your problems as well... The tops of towers problems are cool... Never thought of them that way!)
Log in to reply
@Geoff Pilling – Thanks a lot sir. It's good to know that you liked them :)
Why can't I just multiply 0 by 3 15 times? You told me I start from 0 not 1.
Log in to reply
The problem with that is that we can make 0 on the first move. We are looking for a number which needs a minimum of 15 moves.
"x3"s + "+1"s = 15
We cannot have 3 "+1"s in a row since that could be replaced by well placed "+1" and "x3".
Thus there must be at least 15 / 3 = 5 "x3"s.
With 5 "x3"s the smallest number is
4
0
4
1
0
=
1
1
2
2
2
2
3
because we want to use "x3"s as early as possible to minimize the number.
This is because every "+1" is multiplied by 3 for every "x3" happening after that particular "+1".
If we use 6 shifts the result is greater than 729.
Hence, the solution is
4
0
4
.
I also wrote a program to check every number less than 404 and it says that there are no smaller solutions.
It's good to mention that: × 3 → + 1 → + 1 → + 1
could be always replaced by + 1 → × 3
which yields a shorter sequence
Aren't we allowed to just multiply 0 by 3 over and over again to get zero as the smallest number? Or is the question supposed to be the largest number? I really don't understand the problem.
Log in to reply
The question asks for the smallest number that requires at least 15 moves. Zero could be done in 15 moves (as you suggest), but it could also be done in fewer moves. i.e. It doesn't require 15 moves to get to it.
404 requires at least 15 moves. i.e. There is no way to reach it in only 14 or fewer moves. And its the smallest number that can't be obtained in fewer moves.
Make sense?
I think your logic is correct. Very nice use of number base!
242 can be the answer
it can also be done in 15 steps but can not be done in less than 15 steps.
If I am wrong please correct me
242-1=241-1=240/3=80-1=79-1=78/3=26-1=25-1=24/3=8-1=7-1=6/3=2-1=1-1=0
I have done with backtracking.
Log in to reply
242 can be done in 14 steps:
+1,+1, 3,+1,+1, 3,+1,+1, 3,+1,+1, 3,+1,+1
I think above you have 14 steps as well.
Make sense?
Hi kushal, actually I also tried in the same but reverse of the way you have given and till 242 , 14 moves are used you can also try in that way and then we will get 243 in the 15th move.. so accordingly 243 must be the answer.
Log in to reply
But 243 can be done in much fewer moves: +1 -> *3 -> *3 -> *3 -> *3 -> *3 (6 moves!) :0)
This proof with python
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
|
Output
1 |
|
Nice program! 😎
Relevant wiki: Number Base - Problem Solving
If you think in base 3 , then multiplying by 3 is shifting the numbers to the left and adding a zero on the end.
So, these rules become much simpler, and I'll attempt to show below that 1 1 2 2 2 2 3 is the smallest number that will take at least 1 5 moves, requiring, in this case, 5 shifts, and 1 0 " + 1 "s.
To construct a number, for each digit n from left to right you need to "add n times and then shift once" and then repeat for all digits (not shifting after the last one of course). So, for example (all in base 3 ), to make 1 1 2 2 2 2 3 , you would need to do this: + 1 → × 3 → + 1 → × 3 → + 1 → + 1 → × 3 → + 1 → + 1 → × 3 → + 1 → + 1 → × 3 → + 1 → + 1
That's 15 moves.
I convinced myself that this is the smallest because if you go with 2 2 2 2 2 3 (the largest 5 digit base 3 number) you have 1 4 moves, which isn't enough. So you need to go with six digits. So that's 5 shifts, and the digits need to add up to 1 0 , so 4 of them need to be 2 's. The smallest of these will be with the 1's at the far left, or 1 1 2 2 2 2 3 .
1 1 2 2 2 2 3 = 4 0 4 1 0
Make sense?