Tinsel on a Christmas Tree

Equation of a tree is $-3 x² - 3y² + z² = 0$ . Equation of the tinsel is: $r(t)= \begin {pmatrix} \frac{1}{\sqrt{3}} t \cos(t) \\ \frac{1}{\sqrt{3}} t \sin(t) \\ t \end {pmatrix}$

Length of the spiral is $\frac{t \sqrt{r^2+c^2}}{ 2} \sqrt{1+ \frac{r^2 t^2}{r^2+c^2}} + \frac{r^2+c^2}{2 r} \sinh^{-1} \frac{r t}{\sqrt{r^2+c^2}}$ For values of $r=\frac{1}{\sqrt{3}}, c=1, t=8 \pi$ it gives value of $186.644$ .

Equations can be found here .

Solution II: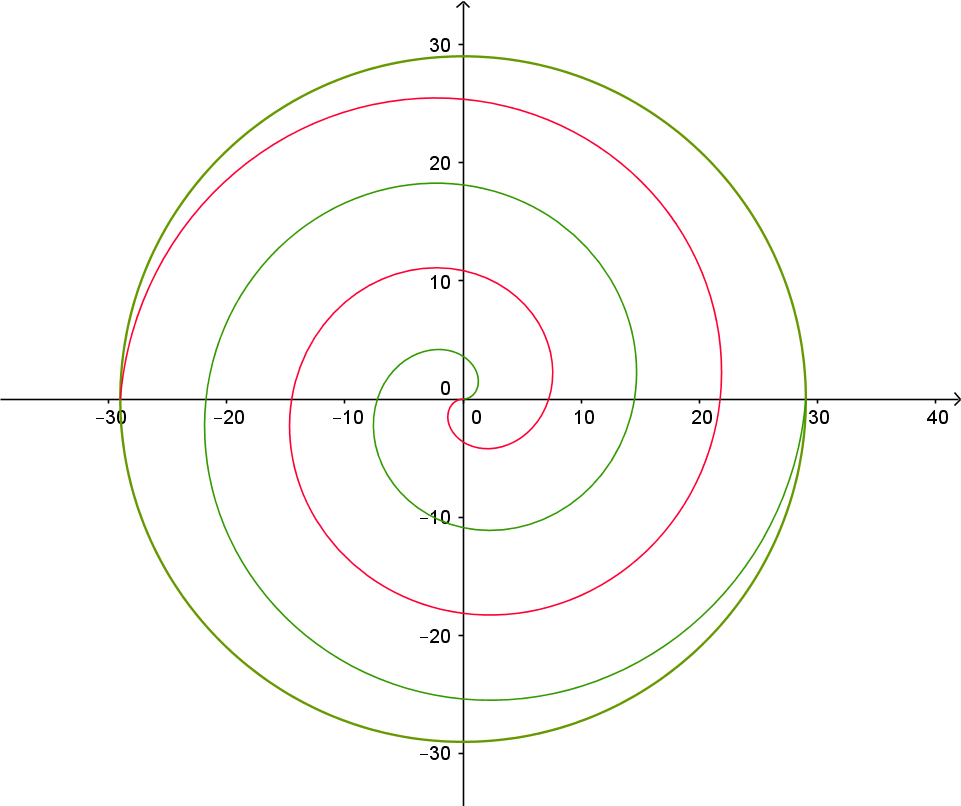

We can also solve it in 2D. The tree has a shape of a cone with $l=2r$ . The lateral surface of the cone is a semicircle of radius $16 \pi \sqrt{3}$ . Tinsel can be thought of as a curve on a cone. Unraveling the cone does not affect the length of the curve. The tinsel will make Archimedean spiral with $a=\frac{4}{\sqrt{3}}$ , with half of the spiral reflected about both X-axis and Y-axis. Length of the Archimedean spiral: $\frac{1}{2} a (t \sqrt{t² + 1} + \sinh^{-1} (t))$ For values of $a=\frac{4}{\sqrt{3}}, t=4\pi$ we can get the value of $186.644$ .