This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
61 solutions
The easiest way I found to think about it is as such. Infinity is not a "number" so we can not perform real calculations on it. So to help ourselves understand it better we use "real" terminology to help ourselves understand it. This is just like how the "house" in the picture below is only a representation. It's a pretty crappy house and nobody would ever live in that house because it has no windows but it is only for representation purposes.
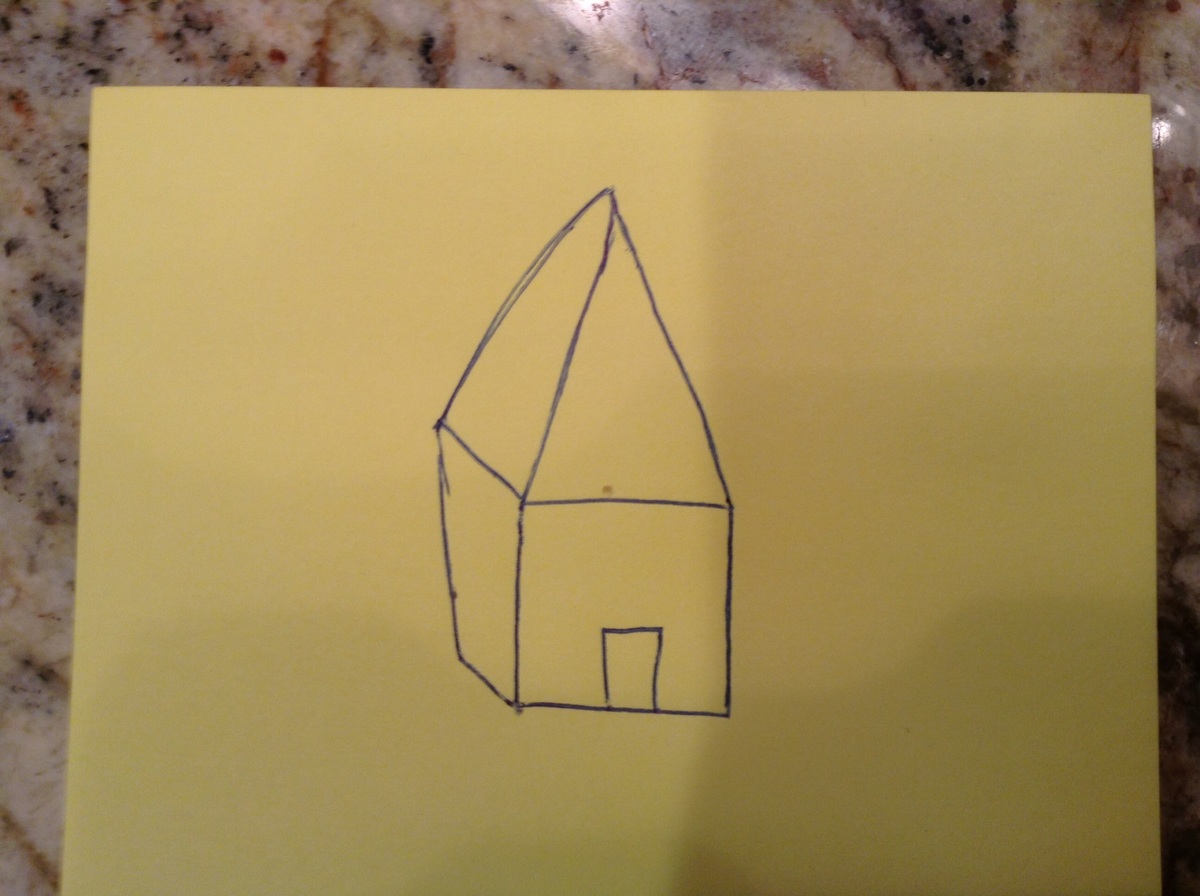
Now to continue with our "algebra" you must remember that these calculations are representative and however not proven fact they simply help us understand infinity better.
Let's say we have a library with an infinite number of books. Every book is named a number and there is a book for every natural number and each is named their respective number. If a customer were to enter the library and say "I wish to borrow all the even numbered books." Then there are an infinite number of even numbered books being borrowed and taken from the library. The calculation for the number of books left being :
(total library books [infinity]) - (even numbered library books [infinity]) = (odd numbered library books [infinity])
Which breaks down to [ infinity - infinity = infinity ]
Now if overnight after all of the book had been returned two burglars were to come in and one of them stole all of the even numbered book so and the other stole all the odd numbered books our calculation for the number of books left over would be:
(Total library books [infinity]) - (even numbered library book + odd numbered library books or also "total library books" [infinity]) = (no books left in the library [0])
Which really breaks down to [ infinity - infinity = 0 ]
Giving the answer to the same " algebraic" equation different outcomes. I am hesitant in using the term "answer" as it is not an answer for it is not one true fact but many. But it all sums up to the fact that infinity minus infinity can only be undefined as there is no "one true outcome"
If you took the time to read through this I thank you and would very much appreciate hearing what other people think of my method!
Log in to reply
Is it fair to say that the infinity symbol represents a set?
Log in to reply
In this case yes it is fair to say but it's probably less confusing for lots of people to replace a set with an infinite library of a well known object
In response to Nick Pan: yes it is fair to label the outcome of the given equation as being a set because infinite is used in modern math as a conceptual value(much like 0), this means that it does not hold place value but still has its own value irrespective to anything else. If a 'larger' infinite is removed from infinite, a negative value would result, if equal infinites are subtracted, they cancel to zero, if infinite is removed from itself, there is still a value resulting as can be seen in previous answers where 1 is achieved as the result however this value is only the outcome because of its minimalistic trait. However it can range between these answers of 0,1 and infinite because the range is already a multiplied infinite (1=0.0000000....001 x infinite) however (0.1=0.000000....001 x infinite) thus providing sequence
To say infinity was a set would be to define it and give it parameters and confines. The equation could be explained as undefined AND infinity, because by nature infinity can't be defined with real numbers
Lets just say that infinity may represent very large number or very small number, so in this case it does matter what kind of number represent each of the infinities in the equation
That is a very nice solution.
It is definitely undefined, because there is no defined answer to this question. Infinity is a term to refer undefined value, not a unit. The answer might be 0 or infinity, but might also be not 0 or infinity. Therefore it is undefined.
Log in to reply
Gud..... For me , it is satisfactry ...... And twll me log 0 - log 0 = ?
Your description is simple. Thanks.
A very didactic approach
well explained
I cant agree with this because your representation of the even and odd numbers of infinity are incorrect to prove this. (total library books [infinity]) - (even numbered library books [infinity]) = (odd numbered library books [infinity]) is the same as [ infinity - infinity = infinity ]. You cant say that this because only the odd numbers would not represent infinity but would represent a subset of numbers that although infinitely big does not contain all the numbers that infinity does.
Log in to reply
infinity also isn't a number as you said, and as I explained this is subtracting an infinite set of numbers from another infinite set of numbers leaving you with no real way to solve the question, hence "undefined." the word "infinity" in my solution isn't used to represent a number but rather express how many numbers there are in that set.
This is absolutely ridiculous! It makes no difference if it is a number or not. If you have anything, and subtract an equal amount of that "anything" it amounts to 0, not undefined. An orange isn't a number but if I have an orange, and I subtract an orange I have 0 oranges. If I have infinite amount of oranges and I subtract infinite amount of oranges it is the same amount. 0. Nothing to contest. If you subtract an equal amount of a what you have the number of what you have left is always 0. If you have an example of where this is untrue please feel free to make yourself look silly and post it for all to see.
Log in to reply
if you have an infinite amount of oranges I think its fair to assume they're not all ripe, meaning you have infinite ripe oranges and infinite unripe oranges. so if you removed all the unripe oranges you would still be left with infinite oranges. now since infinity has no value we use examples like these to help understand. read over what you're saying and what you're commenting on before you start hating.
Slight problem. Infinity works differently from how finite things work. There is the same amount of infinity for the numbers 1, 2, 3, ... as for the numbers 0, 1, 2, 3, ... , but if you take the one from the other, you don't have nothing left, but you have one number left: zero.
Again, the integers are infinite: 0, ±1, ±2, ±3, etc. Take away all the positive numbers, and you still have an infinite number left.
Wow you a 105 years old you must know everything!
Log in to reply
This account is just linked to my Facebook and on my facebook im apparently 105 but really I'm 17
Log in to reply
@Dexter Mackie – 105 and 17 are quite different from each other. Lol
It's actually zero, because when something is taken away from itself, there is nothing left.
Log in to reply
infinity isn't a number, so I'm not "taking it away from itself," but rather removing and infinite amount of numbers from a set which can end in many ways and not just 0.
No as its not ∞₁ - ∞₂ = ? its ∞ - ∞ = 0
This would be the same as X - X = 0 as the X would need to be the same value
Log in to reply
Infinity is infinite. For example, a hotel with infinite rooms is full, and someone comes in for a room for the night; since the hotel is both infinite and full the hotel clerk finds a loop hole. He moves every guest one room over so the new guest gets the first room. He can do this because there is an infinite amount of rooms. This never ends, it is a paradox and a paradox is undefined. So if infinity is undefined, undefined - undefined = undefined; because infinity is not defined as a value the answer could not be 0 because 0 is a value and for an equation to equal 0 the factors must be values. Therefore the difference between infinity and infinity is undefined.
Log in to reply
How can you define a hotel with infinite rooms as full? It defeats the purpose of describing it as infinite because by saying it's full there is at some point a finite number of rooms.
Log in to reply
@Dylan King – That is why it is a paradox, that is exactly my point. Even if it is full at the time. If it is infinite you always have more room to add someone and after you add that person the room becomes full again until the next guest comes. It is a paradox it never ends, such is the definition of infinite.
Log in to reply
@Ash Fard – simple word, logical error... like "deleting" recycle bin...
@Dylan King – It has an infinite number of guests before another guest turns up, it's all very Zen...
@Dylan King – Well not necessarily though, there could just be a comparably infinite number of people staying at the hotel.
@Dylan King – You can have a infinite number of guests
Log in to reply
@Baxter Lopez – No you cannot have a infinite amount of guests because there is a limited amount of people. Logically speaking . Theoretically , yes you could.
Log in to reply
@Karson Bourbeau – Then logically speaking you cannot have a infinite number of rooms as there is a limited amount of space
Log in to reply
@Baxter Lopez – you can not have an infinite number of rooms due to resources not space, the universe is infinite therefore there is infinite space for the rooms
Log in to reply
@Elliot Turner – The universe is not infinite.
Log in to reply
@Michael Wilbur – You cannot know the universe is finite. Have you seen it all?
@Karson Bourbeau – You can't have hotels with infinite space either, this entire situation is a hypothetical
Log in to reply
@Patrick Steirer – Such is mathematics.
@Patrick Steirer – You can because the universe gets bigger
@Dylan King – He's using this explanation: https://youtu.be/Uj3_KqkI9Zo
it sounds like if infinite is multiplied by 0 is undefined hahahaha! zero is the infinity of nothing.
Log in to reply
@Jake Bisnar – Zero times anything, anything at all, is zero. But the form 0 ∗ ∞ is indeterminate because limits of that form can equal zero, infinity, or anything in between (i.e. anything positive but finite).
Log in to reply
@Whitney Clark – so what if 100% of infinite is infinite, and the 90% of infinite is still infinite but weaker, how about the 0% of the infinite?
try this logic, infinite power is existing, but you have nothing so you have 0% of that power!
that example says f(n)=infinity+1n we are discussing infinity-infinity
It wasn't full then
The subtraction you use above has some problems to it. Example: empty set - infinity = empty set ~ 0 {3} + {3} = {3} ~ 1 I use ~ here in response to your interpretation of numbers as the cardinality of a set. Union and set difference are not legitimate cousins of (+) and (-) over the numbers.
This is assuming x is a real number. Since infinity isn't defined in the real numbers, it follows that you can't apply the concept x-x=0 since that rule applies to real numbers only.
you are correct. if definition of infinity is infinity, then the answer is (infinity)-(infinity) = 0 as you said, if you change the definition of one of the infinities, then it would not equal 0
Log in to reply
but to change the definition of one of the infinities would mean changing the equation and how it is written
But the infinity are the same in this question
Infinity is not a number, it is a concept. That is why 0/0 is not infinity; it is undefined.
Except you forget the fact that infinity is only a concept and has no actual value therefore infinity itself is undefined
Log in to reply
Numbers are a concept too. They are intangible. The naturals are defined recursively and they have some well defined operations on them. It's virtue of being a concept alone, is an insufficient excuse for (-) being undefined on it.
cause hazel said that some infinities are greater than other infinities thats why!
How could dat b possible!?? suppose 4 our own considerations 19567893764 is an infinite no. and another no. 63768768838 is infinite! How is the difference 0?
Log in to reply
You cannot consider 1956......... and 6376........... as an "infinite numbers".. There is no such thing as an infinite number. There is only infinity... You are of the idea that infinity like a variable can take different values at different times. No! Infinity is not defined! However, your conclusion is right that the answer it is not zero.
You seem to lack a clear representation for infinity. Does infinity belong to: Integers Set of Sets Some other group
Because (-) is well defined on groups, and it is the identity element over (+) of the group.
how can it equal to 0 when the numbers your subtraction are both unknown? the answer i voted for was Undefined
But how can we define infinity,we can't define it so the and will be undefined definitely
Yeah it's right
Infinity is a very big number ..how big we dont know so we add or subtract two infinite terms the answer is undefined since we just know there value is big...in simple terms if a person know counting till 5 then beyond 6 number are infinity for him
Log in to reply
@Shubham Jain Infinity is NOT a number at all.It is a concept.Because no matter how big a number is,its value is finite.So you are wrong in saying that infinity is a very big number.
Log in to reply
@Abdur Rehman Zahid – Ok.. Then what will be the answer to 1 to the power infinity please explain
Log in to reply
- As no matter how many times 1 is multiplied by itself the answer will be one.
Log in to reply
@Zac Eaton – Yep you are correct but if it is to the power infinity then we are assuming we are multiplying 1 a certain number of times.How many times? that we don't know this reduce we can assume infinity to be a number in terms of mathematics whose value is not known which proves my previous comment to be correct.
Log in to reply
@Shubham Jain – that would be undefined then...
Log in to reply
@Eleazer Adrias – Hi buddy if you are replying this for 1 to the power infinity then nope the answer would be 1 only but if your answer is to the main question yes you are correct.
Wrong. The correct answer is "to infinity and beyond"
What will be the answer if we will add 2 infinities??
Log in to reply
It's not undefined, it's infinity. Big number plus a big number is a big number.
Log in to reply
If we will subtract 2 infinities then also the answer will be infinity or the answer will varry??
The answer would be infinity because it represents an ever-increasing value.
2 infinities is an absurdity-since infinity by itself means a singular entity.BOTH (theoretically) have to be merged to be defined as infinity.
the answer would be 2(infinity)
It is also undefined
I believe that all three answers are acceptable when we take into account the fact that there are multiple infinities. Eg. >0, <0
Log in to reply
The question asked us to consider all infinities (infinites in GENERAL). This means that the two infinities involved could be any infinities.
Not to mention, there are not just multiple infinities, there is an infinity of infinities, and an infinity of infinities of infinities...and so forth.
no, infinity is a single value that continues in both directions infinitely from any start point. therefore x(infinity)=infinity and infinity+x=infinity. You can go on to say that (x+infinity)(infinity)+x=infinity let x=any number
Long back the ancient Indian rishis have stated "If infinity is taken away from infinity, then infinity remains ! This is expressed in a sanskrit mantra in the Upanishads. https://www.youtube.com/watch?v=TodZbfco-j0
Wel......with due respect sir, how do you consider the starting point of infinity in both cases, and not only that, if u r considering the starting point of infinity, then it is nt pure infinity ,.....so I don't agree wid the ans
Isn't infinity an undefined term means it'll go on and on?
If You Added Subscripts To The Problem, Then Everyone Would Have Thought That The Infinities Were Different Values From Each Other. Infinity Is Not A Defined Value, But When You Subtract The Same Undefined Value From Each Other You End Up With Zero(aka Fish1 - Fish2 = Undefined and Fish1 - Fish1 = Zero. So Either The Problem Was Wrong Or The Awnser Was Wrong.
There is only 1 infinity: The universe. The universe it currently getting bigger so it is infinite. One day, when the universe shrinks (this is how it was before the big bang) it will become nothing. Nothing is not zero. Nothing is undefined. (If there is nothing there is nobody there to define it anyway!!)
I Had this doubt, but i got clarified through my note i' ve posted.
but it didnt ask inf(odd)-inf(even) also he didnt ask for inf - (inf-1) he ask inf - inf so i assume the first inf is equal to the second infinite and they are same value that cannot be count
Subtraction of two quantities of same value will always yield zero results.
Log in to reply
Only if they're numbers. Infinity is not a real number. You can remove, from all positive integers, all integers greater than 1 million, which is also infinite, and you get 1000 integers left.
Infinity means limitless time, space and distance. If you remove limitless time, space and distance, nothing will be left or ∞ - ∞ = 0
Log in to reply
Not necessarily. Infinity just means it goes on forever. {0, 1, 2, 3, ...} is infinite, as is {1, 2, 3, ...} But if you take the difference, something remains: the number 0.
I disagree. There are different types of infinite sets, and different rates at which infinity can grow. An example, in a graph with a straight line, both side of the line grow infinitely. When you graph an absolute value, inside the V grows infinitely, but outside of the V grows infinitely, but at a rate three times faster than inside the V. Now that being said, those are separate infinities, they are not the same "number". Now, this without constraints is an infinite number minus an infinite number, their growths aren't mentioned to be different, and you can't say one infinity is all the odd numbers and one is all the even number, as that's not defined. What is showed is the same number minus the same number, which would equal zero.
I dont find that reason to be sufficient, you are not subtracting the numbers 2,4,6,8... from 1,2,3,4... (and for that matter, it would continue in both directions being ...0,2,4... and ...0,1,2... you are subtracting the size of that sequence. put shortly: size of infinity, not contents of infinity.
In the second case it would be (inf - (inf - 1)=1
I just thought that in Maths, 'Infinity' is avoided like the Plague because any operation involving Infinity is Undeterminable
Log in to reply
Not really. If you add or subtract finite numbers to infinity, or multiply or divide by finite nonzero numbers, you get plus-or-minus infinity.
We can write infinity=1/0 So, infinity-infinity = 1/0 + 1/0 So, = 2/0 = infinity I completely agree with ur ans. But tell where am i wrong.
Log in to reply
In elementary school math, you are taught that no matter how many times zero goes into one, you'll never have a remainder that is less than or equal to zero. So you cannot divide by zero.
In algebra, you learn that 1/0 must be the reciprocal of zero, if it exists. But 0x = 1 has no solution, so zero has no reciprocal, and you cannot divide by zero.
If this is calculus, then the limit of 1/x as x->0+ is infinity, but the same limit as x_>0- is minus infinity, which is different, so the limit does not exist.
My thoughts were more like this
If X =Infinity,
X-X=0
Proof that X-X=0
For all X's, X-X=0 (1-1, 2-2, ...)
So, if X-X=0 and X= Infinity,
Infinty-Infinity=0
Sorry about my formatting it's not working well on my phone
Log in to reply
But twice infinity is also infinity, isn't it? So 2x = infinity, too, but 2x - x = x instead of zero.
WTF! infinite - 100% of his own value is = to infinite!? TOTALLY MIND BLOWN AHAHAHAHA!
Log in to reply
Except not all infinities are the same. There are as many positive integers as there are integers greater than 1000; take away the latter and you get, not nothing, but 1000 integers.
But if can resolve equations by cancel out ∞ then ∞-∞ must =0 eg. To resolve x in this simple equation.
x / ∞ = 12 / ∞
Multiply both sides by ∞ you get
x = 12
Just as in
x + ∞ = 5 + ∞
Subtract ∞ from both sides leave you X = 5
demonstrating that ∞ - ∞ = 0
weel, nice solution :)
This would equal 0. Infinity is a set of all real numbers, wether its all ecen or odd, theyd be equal at infinity.
Log in to reply
The integers is also infinite. Take them away from the reals, and what's left is infinite.
what is the value of \infty / \infty?
Log in to reply
The way this question is posed is somewhat inappropriate, as infinity is not a number, but a concept, and thus arithmetic cannot be operated on it. A more appropriate way to pose your question would be, "what is the limit of f(x,y)=x/y as x approaches infinity and y approaches infnity?" The answer, like the original question, is undefined, as there question is underdetermined. For example, we examine 3 additional and separate cases where more information is given: x=y^2, x=y, and x^2=y, which give the solutions infinity, 1, and 0 respectively. Without the additional information, the answer is undefined.
Log in to reply
But why the value of both of the infinities cannot be the same? or why we cannot let it happen?
Log in to reply
@Aap Aap – Well, you're entirely right. Both infinities can be the same size. In fact, the ability for two infinities to be the same size is actually the cornerstone of the limit based calculus we use today. The main issue is that infinity is not a number, but rather a concept, and thus arithmetic cannot be directly applied to it, except through limits. The question is properly posed as, "what is the limit of f(x,y)=x/y as x approaches infinity and y approaches infinity?" One can easily add additional information, without it being inconsistent with the problem. Consider three separate cases: x=y^2, x=y, and x^2=y. If we take the limit as x approaches infinity for all of these cases, y also approaches infinity. Thus, after the limits are applied to f(x,y) something is arrived at that roughly resembles infinity/infinity, and all three cases are consistent with the limit posed. However, before taking the limit, we can substitute the additional equations to get, respectively: f(x,y)=y, f(x,y)=1, and f(x,y)=1/x. Applying these limits to these three cases gives the solutions: infinity, 1, and 0. In this second case (x=y) the infinities are the same size, and thus the solution is 1. The issue is that without additional information (x=y), the other possibilities may also be true, and thus the solution for the generalized "infinity/infinity" is undefined.
Log in to reply
@Kevin Kellogg – Thank you very much for clearing my concept about this.
It's undefined. You can't use division operator on infinity.
Infinity isn't even a number.
€= infinity.. now €-€ = € ( 1-1) = € × 0 =1 therefore answer is 1
Log in to reply
Infinity can't be euro -_-
Infinity is an abstract concept and you can't manipulate it using ordinary math ideas. One good example to prove my point will be that ∞ + ∞ = ∞
Log in to reply
but infinity=-1/12 thus infinity-infinity -1/12 -1/12=0
Log in to reply
@Avishkar Ghadge – Firstly, ∞ = − 1 2 1
1 + 2 + 3 + 4 … is incorrectly assumed to be equal to − 1 2 1
Also, your subtraction is incorrect. It should be − 1 2 1 − ( − 1 2 1 ) = − 1 2 1 + 1 2 1 = 0
Why did you assign your symbol for infinity (I don't have that symbol on my keyboard), as the number 1? Infinity isnt' 1, it is a number (or distance, etc.) that has no end. 1 is an end. Even so, 1-1=0, not infinity. ANYTHING x 0 = 0, therefore infinity x 0 would also = 0.
if ∞ = (n/0) , than ∞ - ∞ = [(n/0) - (n/0)]; now [(n-n)/0] so 0/0 = ∞
Log in to reply
0 (1/0)=0 (inf) which is undefined Remember in limit 12th, the 7..😝
0 n is undefined and it's is not equal to ∞ . So your argument is incorrect. Also, 0 0 is undefined too.
Log in to reply
yes....good argument...0/0, a/o are undefined also infinity-infinity=undefined...
@Arulx Z ohh check it away (n/0) here ! http://www.wolframalpha.com/
Log in to reply
@Jimish Fotariya – Wolfram Alpha shows that because of a convention.
http://www.wolframalpha.com/input/?i=n%2F0
Isn't 0 divided by 0 (0/0) equal 0? You are only asking to divide 0 by 0 once, not an infinite number of times.
To those who might be confused google Hilbert's hotel paradox it will clear the Idea
As infinity is itself ""not defined"' hence any simple operation with infinite is not defined
doesn't infinity - infinity suggest that they have the same magnitude so the answer should be 0
Log in to reply
But this is also true:
infinity - 1 = infinity
So:
infinity - 1 - infinity = 0
thus:
infinity - infinity = 1?!
These are also true:
infinity - 5234.32 = infinity
infinite + 2983480 = infinity
.... you could even say:
infinity + infinity = infinity
or infinity * infinity =.... mind blown
https://www.youtube.com/watch?v=Nfc7G4xKsl8
Log in to reply
Who told you that infinity - 1 = infinity ? It is undefined. That's the point to learn behind this particular question!
Log in to reply
@Bhavik Knight – If you take infinity and subtract 1, out of all the numbers, infinity is the best answer. It's certainly not 3 or 7 and it certainly isn't "I don't know = undefined". Infinity doesn't disappear just because you took 1 away.
If you take an infinite amount of sand, stars, and/or space, and you take away some of that, you'll still have an infinite amount of sand, stars, and/or space. You can look at it and say, yup, there's still a lot of stuff there.
@Bhavik Knight – Infinity is infinite, so it can regenerate.
@Bhavik Knight – i know right
infinty-infinty= a finite number, call it 1 or 0, will be only when infinty is itself defined and a finite number..
Log in to reply
@Rupsa Mukherjee – How?can u explain in another way?
Have you ever seen or measured an 'infinity'? How do you propose that they are necessarily equal???
Yeah but you still could awnswer infinity, it's another way of saying we have no clue, or undifined. It really seems like a trick question
Log in to reply
I too answered infinite.
if that is the case, you'd be breaking a lot of math. let's take for example the operations: infinity plus infinity or infinity minus infinity. If what you say is true, then the answers to both operations would be infinity...But how do you distinguish the difference in those answers, given that one was from addition and the other from subtraction. Because of addition, the "infinity" answer for this operation has to be larger than the two addends. Similarly, the "infinity" for the second operation has to be smaller than at least one of those infinities used in the subtraction, but the act of trying to evaluate the magnitude of infinities breaks the definition of being infinite. In both cases, there's just no way to tell. And even if you could "legally" do that in mathematics, you could still run into trouble with confusion of the relationship of infinities. Therefore, it is best to describe it as "undefined."
Any quantity that cannot be defined in real terms is termed as infinity therefore infinity in any shape where it may appear shall always remain infinity and there cannot be any solution in real terms, therefore logically the answer is undefined
Everyone keeps saying infinity is not defined. Merriam-Webster has several definitions, one of which is "unlimited extent of time, space, or quantity". Just because mathematicians cannot assign a specific, finite number to it (which is what makes it infinite) doesn't mean it is undefined, it just means it goes on and on and on with no end. And, mathematicians just hate that. And even though they have no specific name for it they HAVE assigned a symbol to infinity which stands in place of the number they can't name. Which makes infinity a number, even if we can't name it. And any number minus itself = 0. So infinity (a number) minus infinity (itself) should = 0. Right or wrong, that's what makes the most sense to me.
It can be a large infinite minus a shorter infinite, or a short infinite minus a larger infinite, or equal infinites, or a large infinite minus a larger infinite, you can't define how long will the infinite be or if it can be a normal number, then, it's undefined
Yes like infinite stars - infinite planet... obviously we can't count both of them bt we know that nmbr of stars per planet is more... hnce infinite star is grtr than infinte plnt...
Log in to reply
You are talking about this galaxy only. Please mention that. We don't know counts/ratio of star and planets in other galaxies.
Basically the second infinity would be slightly shorter as it has existed on the page (or as a typed bit of light) for a slightly shorter time. As this shorter time cannot be measured, it is undefined
(1/0) - (1/0) = 1-1/0 = 0/0 = un-defined
We can say that two given quantities are equal if we can measure them. But infinity is an abstract concept and it can neither be measured nor manipulated using ordinary mathematical laws.
One simple example to prove my point is that ∞ + 1 = ∞
Moderator note:
Be careful. One can perform arithmetic on the extended reals (including infinity). In this case, we have 1 + ∞ = ∞ = ∞ + 1 .
It is not true that "two given quantities are equal if we can measure them". It is possible to talk about 2 types of infinities being equal. E.g. there is a one-to-one correspondence between the integers and the rational numbers.
Infinity minus infinity could be infinity or 0. The answer varies with what function is being run or what set is being analyzed. Without a defining function(s) or set(s), there is not enough information to solve the problem - or even define it. There are also different types of infinities. The set of integers and the set of real numbers are both infinite, but differ in size
There are two circles, one with a radius of 1 and the other with the radius of 2. You can fit an infinite number of points into both, but the first circle is still smaller than the second.
In fact we use the term "unspecified" to (infinity - infinity) not undefined, there are 7 quantities are "unspecified" from which 0/0, infinity/infinity, infinity-infinity and 0 times infinity
Infinity is not a number. Just an idea.
The easiest way I found to think about it is as such. Infinity is not a "number" so we can not perform real calculations on it. So to help ourselves understand it better we use "real" terminology to help ourselves understand it. This is just like how the "house" in the picture below is only a representation. It's a pretty crappy house and nobody would ever live in that house because it has no windows but it is only for representation purposes.
(https://d18l82el6cdm1i.cloudfront.net/uploads/9YwKJGl9fQ-image.jpg)
Now to continue with our "algebra" you must remember that these calculations are representative and however not proven fact they simply help us understand infinity better.
Let's say we have a library with an infinite number of books. Every book is named a number and there is a book for every natural number and each is named their respective number. If a customer were to enter the library and say "I wish to borrow all the even numbered books." Then there are an infinite number of even numbered books being borrowed and taken from the library. The calculation for the number of books left being :
(total library books [infinity]) - (even numbered library books [infinity]) = (odd numbered library books [infinity])
Which breaks down to [ infinity - infinity = infinity ]
Now if overnight after all of the book had been returned two burglars were to come in and one of them stole all of the even numbered book so and the other stole all the odd numbered books our calculation for the number of books left over would be:
(Total library books [infinity]) - (even numbered library book + odd numbered library books or also "total library books" [infinity]) = (no books left in the library [0])
Which really breaks down to [ infinity - infinity = 0 ]
Giving the answer to the same " algebraic" equation different outcomes. I am hesitant in using the term "answer" as it is not an answer for it is not one true fact but many. But it all sums up to the fact that infinity minus infinity can only be undefined as there is no "one true outcome"
If you took the time to read through this I thank you and would very much appreciate hearing what other people think of my method!
I am very impressed you can type so well at this revered age
Everything minus everything isn't nothing. It's not defined. It's not possible to take everything from everything conceptually speaking. If you did, you would be left with nothing, which is to say something. Which obviously isn't nothing at all and therefore impossible to determine.
I'm seeing some really clever and intelligent solutions on here, but the main reason I knew it was undefined is because infinity isn't recognised as a proper number, it's a more a concept. I think it's important people know that, although there are some great solutions on here that would make it so easy to understand, so people should definitely check those out.
Suppose
n
is some number, where
∞
−
∞
=
n
.
We know that
∞
+
∞
=
∞
.
So
∞
−
∞
=
n
(
∞
+
∞
)
−
∞
=
n
∞
+
∞
−
∞
=
n
∞
+
(
∞
−
∞
)
=
n
∞
+
n
=
n
∞
=
0
However,
∞
=
0
.
Therefore,
∞
−
∞
=
u
n
d
e
f
i
n
e
d
∞ is nothing but number which is undetermined, even 1 0 1 2 3 4 5 6 7 is ∞ and also 1 0 1 0 0 0 0 0 0 0 0 0 0 0 , so you cannot determine which number actually denotes the infinity. So that's undetermined.
Infinity is just a concept, never treat it as a real number.
we know something divided by 0 is called infinity . so if make infinity - infinity =0/0 its undefined
I think of it this way: infinity - infinity could equal 0, if the two different infinities diverged at the same rate. However without any functions the value is undefined, because we have no knowledge of the rate that the infinities were reached.
Although it wasn't an option, I think it should be indeterminate, which is different from undefined. See https://en.wikipedia.org/wiki/Indeterminate_form. Because for different infinities if you will there are different solutions rather than always being undefined it is considered indeterminate.
Any rules of mathematics is now applicable with 0 & infinity
One common mistake is that people make is the idea that infinity is a number. It's not a number but a concept. It means to go on without end. You can't treat it like a numeric value because that would be giving it an end. Thus an operation such as this isn't possible
It actually depends on preceding limiting variable. Suppose there is a variable 'a' limiting to infinity and variable 'b' also limiting to infinity. 'a' is defined as a = क(a) and b is defined as f(b). The Two different function can approach infinity differently. So a - b depends on the value of k = क(a)/f(b) i.e. if k = 1 then a - b equals 0 i.e. constant value. If k > 1 then a - b equals a. and k < 1 then it is -b.
Lol .... I remembered the solution from fault in our stars that one infinity can be greater or less than other infinity so its should be undefined
Am not sure of this. Since infinity =1/0. Therefore infinity-infinity =1/0-1/0=0/0. But 0/0=undefined. Then the answer is undefined
To be technically correct, the answer should read "Indeterminate", not "Undefined". The word "Undefined" is for expressions that have NO answer, like 5/0, since there is NO real number that you can multiply by zero to get five. The expression 0/0 is indeterminate, since ANY number times zero equals zero. Many commenters have shown how you can remove a set of infinite cardinality from a set of infinite cardinality and leave zero, some finite number, or an infinite number of elements, so there is not ONE answer, but an infinite number of possible answers and thus it is indeterminate.
i just thought of infinity as 'unknown' so if you take unknown-unknown The answer is unknown or in other words 'undefined'
∞ is unreal, so any calculation with it is meaningless. Also, there's no definition of Infinity's calculation, so undefined
The infinity number doesn't represent any particular number, so you don't know the answer. That's why it is undefined. Simple.
Although it may seem that infinite minus infinite equals zero (after all, they both are the same numbers) infinite is not a defined number. It keeps growing. As taught in elementary school, x-x=0- for defined numbers. But as stated before, infinite is not a defined number. Infinity grows to a constant number, then grows again to another constant, then grows again. The other infinity is the same; it may lag behind, then catch up, etc. It's like watching a never ending horse race; one horse may take the lead, another may catch up, then the first will take the lead again, etc.
Infinity=1/0 So infinity-infinity =1/0-1/0=0/0, which is not defined
First of all "infinity" is something which is not defined.therefore any function involving "infinity "is not defined!!..that's wat I thought!;p
Infinity taken away from infinity= undefined. How could you measure infinity minus infinity? How can that be given a value? The first thought would be 0. Although, 0 is measurable. What if there wasn't a 0 to measure?
I also saw this as Reality - Reality=? (Reality, everything in literal existence, all matter). If there was nothing then you couldn't measure it because there wouldn't be anything or anyone to measure it. Thus it makes no sense, thus it's undefined.
Moderator note:
There is actually a deeper reason to why ∞ − ∞ is undefined. In the first place, the subtraction operator has only been defined on real numbers, and (as it turns out), cannot be extended to ∞ .
infinity is not a quantity but rather it is a direction.
Infinite number means a very very extremely large number . So if a very large number is subtracted from another large number then we cannot actually predict the result. It can be 0 , infinite, or a finite number. Therfore the answer is undefined.
Technically, infinity isn't a real number, so anything involved with it isn't really a real number either.
We. Don't known that undefined what is number so undified minus undefined is undefined thank frnnds
Well if we see at this way that infinity is equal to 1/0 then the solution is quite clear. And answer will be unrefined
It is one of the indeterminate form
that is undefined cause when we talk about infinity , we talk about something which is very large but we can't say definitely what the number is ............ INFINITY is something which is larger than the number the number we r thinking instantaneously................ so its absurd to guess what infinity minus infinity will bw
Simply put, infinite numbers cannot be either zero or one, therefore, so subtracting infinity by itself is indeterminate.
Undefined is the only technically correct answer, as infinity is a placeholder for undefined equations and doesn't have a value. Although, in more advanced physics you can assign a value to an infinite sequence defined as {1+2+3+4+...}. This can be done in a very specific way (no, not as "done" by numberphile), which comes to -1/12. Considering that, you could subtract the values that you assigned to come to 0, but that isn't infinity minus infinity, simply the value of one sequence subtracted by itself.
Imagine it like this. A rabbit and a tortoise are in an infinite race. They will continue to run for infinity but will obviously travel at different speeds. At any point of time the rabbits infinity will be larger that the tortoises due to the rabbit being faster. This means that you can have an infinity larger than another infinity. The answer is undefined because it is unknown the 'largeness' of the infinities.
say if they go backwards(subtraction) then they reach same point, which is zero.
I thought infinity - infinity was indeterminate? Is that the same as undefined or am I wrong?
answer is undefined but according to Vedic mathematics its infinity
Suppose 5/0 -3/0 Then this can be written as 5-3/0 which is equal to infinity. There we can say infinity - infinity = infinity
Your math would be wrong in your example, even if you defined 0 as infinity; which it isn't. You always do multiplication and division before you do addition and subtraction in an equation. So,in your example you would first divide 3 by 0, which would be 0. Then you would do your subtraction, 5 - 0. Which would be 5.
Archisman , bro you have given a wrong proof
Infinity can be any set of numbers making the answer improbable to find. Therefore making it undefined. Infinity is not a variable that can be supplemented with only one number. EG the variable "x" could be substituted with the number 5 and it would have to stay at 5. With infinity, it can be any possible number, making infinite amount of possible solutions.
Man, this is basic Calculus. Correct answer is UNDEFINED. No need to chat here if you do not have basic understanding of the limit concept. Infinite is a tool only with clear purpose to deal with functions (or other math entities) that have a tendency to grow indefinitely when argument approaches a given value (E,G, tan(Pi/2)) So please keep away from posting nonsense if you do not have the proper induction in this kind of matters.
Since infinity is undefined value for any number ,therefore the given expression can neigher be ZERO,nor any other value and it is defined....Ans
A growing number cannot be subtracted by a growing number so if we hold this to be true the answer would also be changing so it cannot be defined. Undefined is correct.
Infinities can be created from any range of numbers. For example, between the two numbers 1 and 2 there are an infinite amount of numbers but the difference between them is only 1. Also, between the numbers 1 and 100 there are also an infinite amount of numbers, however their difference is 99. So it is undefined because one infinity can actually be smaller than another
It is undefined because the size of the infinitys. Can change, we can talk about different infinitys as we don't know yet how or of what an infinity is composed. We just know it's really big and we cannot understand it
Infinity isn't really a number, so you can't do the same things with it. Infinity is "how many" of something that cannot be counted because there is no end to it. Since infinity isn't a number, what "minus" means isn't really clear.
Infinity doesn't have a value. For example, if you keep counting upwards in a number line in whole real numbers, there are infinite potential values. There are also infinite potential values between 0 and 1. Since it's impossible to define the value of infinity it must also be impossible to define infinity minus infinity.
Infinity=1/0 (as 1/infinity=0) We know 1/0= not defined then infinity is said to be not defined not defined - not defined = not defined Therefore infinity-infinity=not defined.
There are differents infinities ? Or is it the largest number ? We do not have any idea about infinity ? I don't understand why is undefined
There is somewhat of a flaw in this question. The issue is that infinity is not a number, but rather a concept, and thus it is inappropriate to pose the question as "what is infinity minus infinity?" A more appropriate way to pose this question would be, "What is the limit of f(x,y)=x-y as x approaches infinity and why approaches infinity?" The answer depends on the aleph of infinity of x and y. With additional information, such as x=y, or 2x=y, or x=2y, we can obtain different answers, such as 0, infinity, or negative infinity. Without additional information, the question is undetermined and therefore the solution undefined.
Infinity isn't really a number, so you can't do the same things with it. Infinity is "how many" of something that cannot be counted because there is no end to it.
Moreover since ininifty is a number , you are indefinite of what minus is then.
The answer wouldve been zero if both the numbers subtracting were same.
The answer could be infinite. If you have all numbers, and you remove all even numbers, you still have infinitely many left.
There would be more possiblities with negative numbers. Thus, subtracting infinity minus infinity isnt really definite
Couldn't you use l'hopital's rule to argue that the answer is zero?
l'hopital's rule works with functions and limits that originally go to 0/0 or infinity/infinity. Since we don't have functions or division/multiplication it doesn't work here.
Infinity is not a number so we dont know what we are going to subtract . Its just a idea where we cannot reach
Infinity means something which never ends..so its not unidentified number. It means that infinite - infinite , infinite + infinite , infinite * infinite and infinite / infinite . Ans for all is infinite.
Log in to reply
That ignores the concept that there are different types of infinity. If I were to do 2+2+2+... continually and 1+1+1+... continually as well, the former would approach an infinity twice as large as the latter infinity. Therefore, if we were to do the former divided by the latter, the answer would be 2. Not all operations involving infinity turn out to be infinity. The type of infinity must be specified
Log in to reply
In this question, I think the values are given as being equal as it says "infinity means infinate in general. That statement makes them equal. Answer is 0
Log in to reply
@John Perritt – I interpreted infinity in general as the concept of infinity itself rather than a specific type of infinity, which is why I chose undefined.
To see that ∞ − ∞ is undefined, let's take a look at some common sets that are infinite. First, consider the natural numbers N = { 1 , 2 , 3 , 4 , . . . } and the subset of even numbers { 2 , 4 , 6 , 8 , . . . } . Note that these sets are the same size because for every natural number n there is a corresponding even number, namely 2 n .
Now, if you remove the even numbers from the natural numbers, then you are left with only the odds: { 1 , 3 , 5 , 7 . . . } , which will also be same size. So, in this sense we removed an infinite number of elements and were left with an infinite number of elements, so you might say ∞ − ∞ = ∞ .
However, suppose we now remove the set { 2 , 3 , 4 , 5 , . . . } from the natural numbers. This time we are removing and infinite set from an infinite set to leave only one element, so you might say ∞ − ∞ = 1 . This shows that the difference isn't well defined in general and doesn't even take into account uncountable infinities.