To The End of The Line
 n
→
∞
lim
k
=
1
∑
n
n
4
+
k
4
k
=
d
a
ln
(
b
+
c
)
n
→
∞
lim
k
=
1
∑
n
n
4
+
k
4
k
=
d
a
ln
(
b
+
c
)
The above summation is fulfilled for positive integers a , b , c , d , with a , d coprime and b square-free.
What is the value of a + b + c + d ?
The answer is 6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Did the same! But 5 is a really good number, better than 6 . Why did you just consider that 1 in front? 5 would be the best of answers.
Log in to reply
You may be right, but I thought that 5 was going to be easy to just guess at, so I added an extra factor to make people think twice. Maybe if I wrote the expression as
d a ∗ ln ( b + c )
it would make 6 the "better" answer. What do you think?
Log in to reply
Yeah! That's fine! I was just saying because number 5 looks much prettier than number 6 . But yeah, here 6 is better due to the fact that it makes the problem "a little"(just a little) more fun. And that way, you made the answer an even(so every "Adrian Monks" would love that) :)
Log in to reply
@Kartik Sharma – Haha. Yes, I've always found 5 to be a "pretty" number as well. :) And I knew Monk had lots of phobias but I didn't know odd numbers was one of them. How odd. :P
Exactly...!!!! Done the same process.
Same way, but I just substitute x 2 = t in integration.
Rewrite the limit/sum as
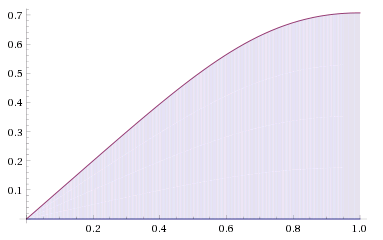
lim n → ∞ ⎝ ⎛ n 1 k = 1 ∑ n 1 + ( n k ) 4 n k ⎠ ⎞ .
We can then see that this is a right-hand Riemann approximation of the integral
∫ 0 1 1 + x 4 x d x .
As the integrand is Riemann integrable, our limit will be equal to this definite integral.
To solve this integral let x 2 = tan ( θ ) . Then 2 x d x = sec 2 ( θ ) d θ , and thus the integral (without bounds) becomes
2 1 ∫ 1 + tan 2 ( θ ) sec 2 ( θ ) d θ = 2 1 ∫ sec ( θ ) d θ = 2 1 ln ∣ sec ( θ ) + tan ( θ ) ∣ =
2 1 ln ∣ 1 + x 4 + x 2 ∣ ,
which when evaluated from x = 0 to x = 1 yields a value of 2 1 ∗ ln ( 2 + 1 ) .
Thus a + b + c + d = 1 + 2 + 1 + 2 = 6 .