Too Complex! Part- II
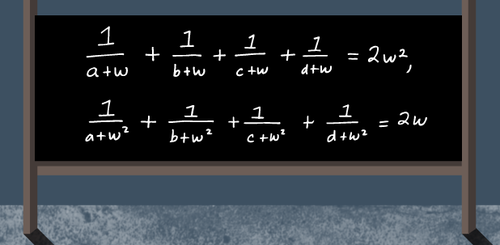If Real numbers a, b, c and d (none of which are
−
1
) satisfy the following conditions:
a + ω 1 + b + ω 1 + c + ω 1 + d + ω 1 = 2 ω 2 , a + ω 2 1 + b + ω 2 1 + c + ω 2 1 + d + ω 2 1 = 2 ω .
To 2 decimal places, find the value of -
a + 1 1 + b + 1 1 + c + 1 1 + d + 1 1
Note that ω and ω 2 are the complex cube roots of unity other than 1.
The answer is 2.00.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Can you prove that there are many solutions? Or Can you please give an example of another solution? Thanks.
@Avineil Jain Do you have an argument for why the sum must be 2 (if any of the values are not 1)? I agree with Jack that you are unlikely to have enough restrictions on the set of values.
@Jack D'Aurizio I would prefer if none of the values are − 1 , since that would make ∑ a + 1 1 undefined. What is possible (assuming the problem is true) is that any path of solutions that approach ( 1 , − 1 , − 1 , − 1 ) would yield a sum of 2.
Log in to reply
Sir, Consider the equation a + x 1 + b + x 1 + c + x 1 + d + x 1 = x 2
From the given conditions, ω and ω 2 satisfy it.
We just have to prove 1 is a root of this equation. Simplifying the expression, we get-
2 x 4 + x 3 ( a + b + c + d ) − x ( a b c + a b d + a c d + b c d ) − 2 a b c d = 0
It is a biquadratic. So it has 4 roots, 2 of which are ω and ω 2 . Let the other roots be p and q.
Note that coefficient of x 2 is zero. So,
p q + ω 3 + ( p + q ) ( ω + ω 2 ) = 0
p q + 1 − p − q = 0
This means that either p=1 or q=1. So, 1 is a root of the equation and hence,
a + 1 1 + b + 1 1 + c + 1 1 + d + 1 1 = 1 2
Log in to reply
This is how I did it, although I thought of the end of the argument slightly differently: the fact that that quartic has ω and ω 2 as roots means that it's divisible by x 2 + x + 1 . The quotient is another quadratic polynomial, and setting the x 2 coefficient of the product with x 2 + x + 1 to 0 shows that the sum of its coefficients is 0 . So 1 is a root of the polynomial.
And I did want to point out that if you wanted to make the problem even harder, you could have omitted the second equation, since it automatically follows from the first one by complex conjugation!
Log in to reply
@Patrick Corn – That is a very nice interpretation!
@Patrick Corn – thank you, did not think of that!
Thank you for your solution. I have removed the banner from your question.
Log in to reply
@Calvin Lin – @Calvin Lin Did you put the awesome picture on this sum?!
@Jack D'Aurizio See my solution below
@Avineil Jain that's a nice solution. Thanks for the solution. I couldn't solve that question.
w^2 =1..therefore 2w=2 (correct answer)
we know that 1+w+w^2=0,
2*w^2=2,
2+2 w+2 w^2=2*(1+w+w^2)=0
sum of all the three equation =0
Hence 2.000 is the required answer.
We have 1 / (a + x) + 1 / (b + x) + 1 / (c + x) + 1 / (d + x) = 2 / x. Now keeping x=1, we get our answer 2.
You invite the question of how?
well how can u prove that x=1 is a root of the equation?
a,b,c,d belong to R so for a=b=c=d=1, x=1 is a root.
I think the correct answer is that we cannot predict the value of a + 1 1 + b + 1 1 + c + 1 1 + d + 1 1 . There are plenty of ( a , b , c , d ) ∈ R 4 such that a + ω 1 + b + ω 1 + c + ω 1 + d + ω 1 = 2 ω 2 - notice that the second equation a + ω 2 1 + b + ω 2 1 + c + ω 2 1 + d + ω 2 1 = 2 ω follows from the first one by complex conjugation. All we need to fulfill the first equation is: c y c ∑ a 2 − a + 1 a = 0 , c y c ∑ a 2 − a + 1 1 = 2 , so ( a , b , c , d ) = ( 1 , − 1 , − 1 , − 1 ) is a solution, and there exist solutions ( a , b , c , d ) with a + 1 1 + b + 1 1 + c + 1 1 + d + 1 1 unbounded.