Well, i don't think this is too easy
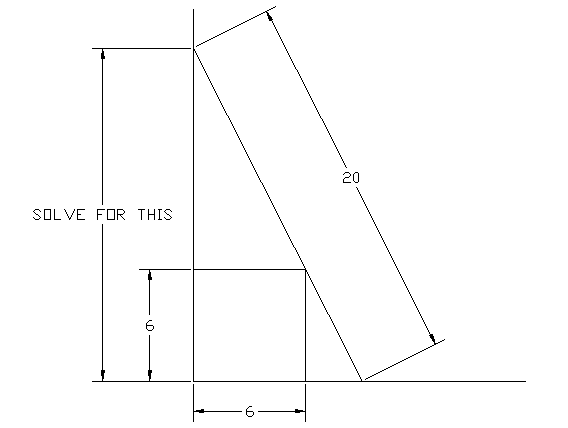Given in the figure is a
20 foot ladder
leaning against a wall, at the bottom is a
6 by 6 by 6
cube
touching the ladder at one point and pushed against the bottom of the wall.
You need to solve for the height
marked in the figure.
If height is 'H', enter your answer as
[H]
{where [x] is the floor function}
I did not make this problem and is taken from here
The answer is 17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
nice :) ........ this is what i was talking about in the discussion of the other solution
Log in to reply
shit, i didn't write the floor function. i wrote the height
Well that seems to be easy and it it easy.
Trigo
N
o
t
e
t
h
a
t
B
E
=
2
0
c
o
s
(
θ
)
a
n
d
E
C
=
F
C
=
6
a
n
d
B
C
=
E
B
−
E
C
=
2
0
c
o
s
(
θ
)
−
6
I
n
t
r
i
a
n
g
l
e
B
C
F
w
e
h
a
v
e
B
C
C
F
=
t
a
n
θ
p
u
t
t
i
n
g
v
a
l
u
e
s
w
e
h
a
v
e
t
a
n
θ
=
2
0
c
o
s
θ
−
6
6
A
l
l
i
s
l
e
f
t
t
o
s
o
l
v
e
f
o
r
θ
.
⇒
1
0
s
i
n
θ
−
3
t
a
n
θ
=
3
⇒
5
s
i
n
2
θ
=
3
(
s
i
n
θ
+
c
o
s
θ
)
⇒
−
5
c
o
s
(
2
θ
+
2
π
)
=
3
2
s
i
n
(
θ
+
4
π
)
P
u
t
θ
+
4
π
=
x
O
u
r
e
q
u
a
t
i
o
n
b
e
c
o
m
e
s
−
5
c
o
s
(
2
x
)
=
3
2
s
i
n
(
x
)
⇒
1
0
s
i
n
2
(
x
)
−
3
2
s
i
n
(
x
)
−
5
=
0
⇒
s
i
n
(
x
)
=
(
2
0
3
2
+
2
1
8
)
⇒
x
=
sin
−
1
(
2
0
3
2
+
2
1
8
)
≈
7
1
.
8
7
0
o
r
1
0
8
.
1
2
0
⇒
θ
≈
2
6
.
8
7
0
o
r
6
3
.
1
2
0
.
⇒
h
=
2
0
s
i
n
θ
≈
9
.
0
4
o
r
1
7
.
8
4
.
⌊
h
⌋
=
9
o
r
1
7
,
I
s
t
i
l
l
d
o
n
′
t
k
n
o
w
w
h
y
9
i
s
n
o
t
t
h
e
a
n
s
w
e
r
.
9 . 0 4 0 5 2 . . . is the other answer, because the floor could be the wall, while the wall is the floor. In other words, flip the ladder. The figure is already provided.
Log in to reply
right!!. :) ..... 71.87 and 108.12 are complementary angles
i get 9 wrong wtf
it is easy, of course, when you use trigonometry :p ........ but i had tried this 2 years back without even the least conception of trigonometry!!........ hence, the name (try without trigonometry, you will enjoy it!)
Log in to reply
Well, of course, H can be solved directly with this equation:
( H − 6 ) 2 + 6 2 + 6 2 + ( H − 6 6 2 ) 2 = 2 0
which leads to the same results.
Log in to reply
Here's your solution without trignomerty
Log in to reply
@Ronak Agarwal – Ronak, the equation may look straightforward, but it's tedious to get at the roots, so doing it by trigonometry might be a more expedient route to a numerical answer.
Log in to reply
@Michael Mendrin – I know that I just told it easy because the solving part can be left to wolfram alpha.
@Michael Mendrin – YES !... i was stuck there ......... its tricky! :)
whoa! yes ........ the same :p
A different approach without trigonometry---
Let ABC be the triangle with angle B 90 degrees. Let BDEF be the square with D on AB (top of cube on wall) and F on BC (cube bottom)
Let x be the length of line segment AD, and let y be the length of line segment CF.
1)Because of the similarity of the triangles ADE and EFC, the following holds: x:6=6:y
So xy=36 . Also x=36/y and y =36/x
2)By Pythagoras,
(x+6)^2 + (y+6)^2 = 20^2
(x^2+72+y^2) + 12x+12y=400
Using xy=36,
(x^2+2xy+y^2) +12x +12y=400
(x+y)^2 +12(x+y)-400 =0.
Solving quadratic equation (x+y) = 14.88
3) x=36/y so x+(36/x)= 14.88
x^2+36= 14.88x
x^2-14.88x+36=0
Solving quadratic equation,
x= 11.83 or 3.04
The height of wall where ladder touches is 11.83 + 6 = 17.83
Floor function = 17.