Too much brute force can kill you!
ξ = cos 0 ∘ + cos n ϕ + cos n 2 ϕ + ⋯ + cos n ( n − 1 ) ϕ + cos ϕ sin 0 ∘ + sin n ϕ + sin n 2 ϕ + ⋯ + sin n ( n − 1 ) ϕ + sin ϕ
The above ratio can be expressed in a simplified form. You may want to find that form first.
If n = 7 1 and ϕ = 7 1 ∘ , then what is the value of ξ ?
Give your answer to three decimal places.
The answer is 0.713.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
Hi,
My solution was based on the very same idea, but with slightly more transparent grouping (at least for me). It is just a miniscule nuance, but it may bring more clarity, that is why I am pointing it out, together with the rationale behind it.
I grouped s i n ( 0 ° ) with s i n ( 7 1 ° ) and s i n ( 1 ° ) with s i n ( 7 0 ° ) ... and s i n ( 3 5 ° ) with s i n ( 3 6 ° ) to see what would fall out. It is a good practice to merge the terms from the "opposite ends." Because of symmetry, there are nice things often emerging, such as with arithmetic series - the sequence 1 + 2 + . . . + ( n − 1 ) + n becomes summable after regouping ( 1 + n ) + ( 2 + ( n − 1 ) ) + . . . .
When I saw that 2 ∗ s i n ( 7 1 ° / 2 ) factored out and the remaining terms were looking suspiciously similar to the denominator, but with the half degrees "off," I tried out what would happen, if I did the same thing as I have done above also below. Again, I was searching for some like pattern. And, voilá, there it was, all factored out.
Message: The last need to make friends with the least for stuff to work out well :)
P.S.: @Jahid, you have picked a kind of magical title ;)
Log in to reply
Thanks for sharing your approach.
I'll tell you a little bit about the birth of this problem. I was solving another geometry problem a few days ago. Somehow the problem was solved. But, there was a missing link. I imposed that the ratio ξ depends only on ϕ without any proof.
And, I posted this problem when I solved it. At one stage, I used brute force which came out to be brutal. That's why I chose the name. :)
Log in to reply
Thanks for the reply. It is a nice problem. What was the original one, can you post it?
As for the title, I thought it is allusion to the Queen's song but apparently not.
Log in to reply
@Stanislava Sojáková – https://brilliant.org/problems/interpreting-congruent-angles/ The problem is named "Interpreting congruent angles".
The most interesting part here is that ξ doesn't depend on n . ;) You may call this "Atomsky's sine-cosine identity". :v
Log in to reply
An almost same problem is in the 1st chapter book of physics by resnick and halliday where there was Φ = 2π. :D
Simple problem. Use Lagrange's identities to generalize the numerator and the denominator and cancel out the common factors. The answer comes out to be tan ϕ / 2 . Plug in ϕ = 7 1 ∘ to get 0 . 7 1 3 2 9 as the answer.
Did the same!!!. Lagrange's identity greately simplifies some summations!
Would you please explain how you used Lagrange's identity? An article explaining this method or topic would also do. Thank you.
Log in to reply
All right. I'm feeling lazy to type out the latex codes, so I'll give you the image cutout from Wikipedia instead-
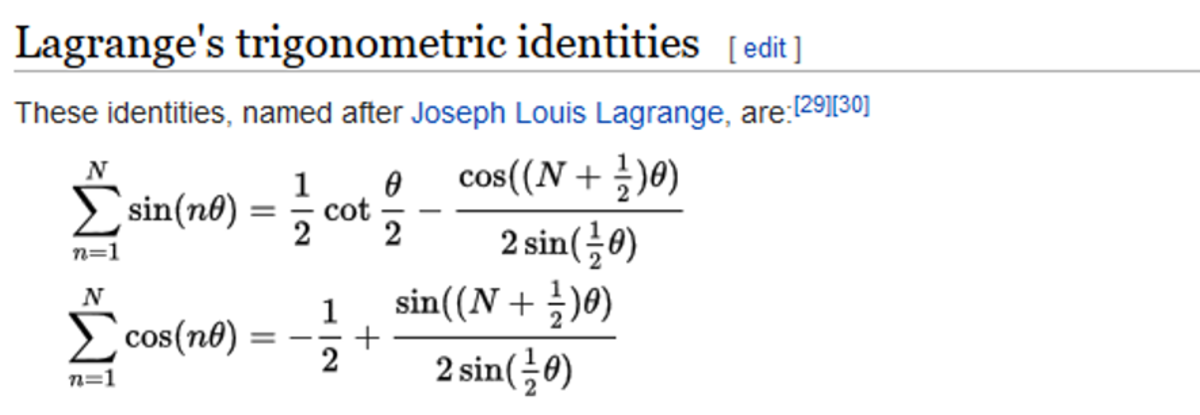 Just simplify the two keeping in mind that
θ
=
n
ϕ
and that the denominator has an extra
1
from
cos
0
which doesn't come into the general formula. The common terms will cancel and leave out
tan
2
ϕ
. Easy as pie.
Just simplify the two keeping in mind that
θ
=
n
ϕ
and that the denominator has an extra
1
from
cos
0
which doesn't come into the general formula. The common terms will cancel and leave out
tan
2
ϕ
. Easy as pie.
In general,
sin ( a ) + sin ( a + d ) + sin ( a + 2 d ) + . . . + sin ( a + ( n − 1 ) d ) = sin ( d / 2 ) sin ( a + 2 ( n − 1 ) d ) sin ( n d / 2 )
And,
cos ( a ) + cos ( a + d ) + cos ( a + 2 d ) + . . . + cos ( a + ( n − 1 ) d ) = sin ( d / 2 ) cos ( a + 2 ( n − 1 ) d ) sin ( n d / 2 )
Using these,
cos ( a ) + cos ( a + d ) + cos ( a + 2 d ) + . . . + cos ( a + ( n − 1 ) d ) sin ( a ) + sin ( a + d ) + sin ( a + 2 d ) + . . . + sin ( a + ( n − 1 ) d ) = cos ( a + 2 ( n − 1 ) d ) sin ( a + 2 ( n − 1 ) d ) = tan ( a + 2 ( n − 1 ) d )
Number of terms are n + 1 and and we have a = 0 ∘ and d = ϕ / 2 , hence we end up with tan ( ϕ / 2 ) = tan ( 7 1 ∘ / 2 ) ≈ 0 . 7 1 3 .
Since in our problem n ϕ = 1 we can rewrite ξ more simply as
ξ = cos 0 + cos 1 + ⋯ + cos 7 1 sin 0 + sin 1 + ⋯ + sin 7 1
where here and from now on we will take it for granted that the arguments are in degrees.
Using Euler's wonderful formula e i θ = cos θ + i sin θ we can see that the numerator and denominator of ξ are the imaginary and real parts of the series
x = e 0 + e 1 i + e 2 i + ⋯ + e 7 1 i
This is a geometric series with first term equal to one, common ratio e i and 72 terms, so it is easily summed with the g.p. formula to give
x = e i − 1 e 7 2 i − 1
The denominator can be made real by multiplying by its complex conjugate, to give
x = ( e i − 1 ) ( e − i − 1 ) ( e 7 2 i − 1 ) ( e − i − 1 ) = ( e i − 1 ) ( e − i − 1 ) e 7 1 i − e 7 2 i − e − i + 1
The answer to our problem is the ratio of the imaginary to real parts of this expression. Since we need only their ratio we can ignore the purely real denominator and use Euler's formula again to get
ξ = cos 7 1 − cos 7 2 − cos ( − 1 ) + 1 sin 7 1 − sin 7 2 − sin ( − 1 ) = 0 . 7 1 3
Easy prob try solving orally try to make a general formula for ap os sine and cos


Relevant wiki: Sum and Difference Trigonometric Formulas - Problem Solving
At first, think about a small case.
Let, n = 5 . So, the ratio becomes, ξ = c o s 0 ∘ + c o s 5 ϕ + c o s 5 2 ϕ + c o s 5 3 ϕ + c o s 5 4 ϕ + c o s ϕ s i n 0 ∘ + s i n 5 ϕ + s i n 5 2 ϕ + s i n 5 3 ϕ + s i n 5 4 ϕ + s i n ϕ or, ξ = 1 + c o s ϕ + c o s 5 ϕ + c o s 5 4 ϕ + c o s 5 2 ϕ + c o s 5 3 ϕ s i n ϕ + s i n 5 ϕ + s i n 5 4 ϕ + s i n 5 2 ϕ + s i n 5 3 ϕ Using the formula for compound angles, we have ξ = 2 c o s 2 2 ϕ + 2 c o s 2 ϕ c o s 1 0 3 ϕ + 2 c o s 2 ϕ c o s 1 0 ϕ 2 s i n 2 ϕ c o s 2 ϕ + 2 s i n 2 ϕ c o s 1 0 3 ϕ + 2 s i n 2 ϕ c o s 1 0 ϕ Now, you can factor the common terms [ s i n 2 ϕ in the numerator and c o s 2 ϕ in the denominator] out of the rest. And, you'll see the rest is the same both in the numerator and the denominator. So, they will cancel each other out. Hence, ξ = c o s 2 ϕ s i n 2 ϕ = t a n 2 ϕ This is true for all n . The general case can be derived in the same way. For, all even n , the term s i n n 2 n ϕ or c o s n 2 n ϕ is readily in the form s i n 2 ϕ or c o s 2 ϕ . As you can see, ξ depends only on ϕ . Now, putting ϕ = 7 1 ∘ in the formula for ξ we get ξ = t a n 2 7 1 ∘ ≈ 0 . 7 1 3