Topping Tetrahedral Ten

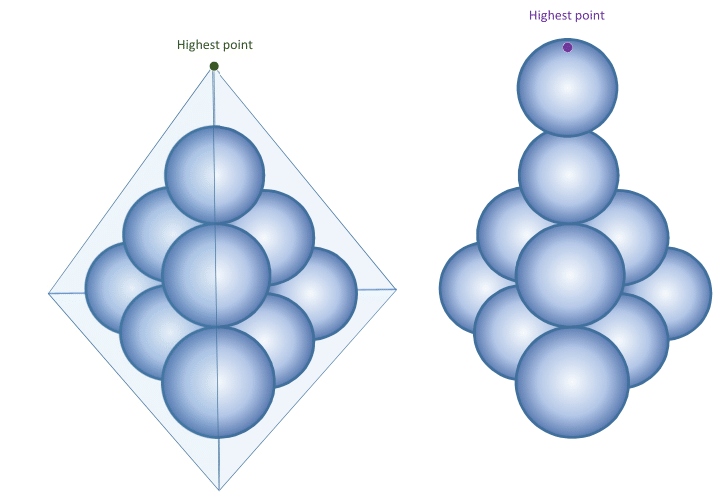
Ten identical spheres are packed as above. You can either encase the entire stack in a tightly fitting tetrahedron, or you can balance one additional sphere on top. Which will be higher off the ground, the top vertex of the tetrahedron or the top of the additional sphere?
Details
-
Each of the spheres in the top two layers of the original arrangement is supported by three spheres which are all tangent to one another.
-
The entire arrangement sits on a level ground.
-
Each face of the encasing tetrahedron is tangent to six of the spheres in the stack.
-
The additional sphere is identical to the others, is supported only by a single sphere below it to which it is tangent, and its center is directly above the center of the sphere below it.
Top image credit: Etsy.com
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
If we consider the edge of the tetrahedron, it is not tangential to the spheres, but a slight distance away. This helps explain why the highest point of the tetrahedron is so much further away than one might initially expect.
For an analogous scenario, think about drawing a cube around a ball with the faces of the cube touching, vs with the edges of the cube touching.
Can I get feedback on the new images? Any suggestions for how we can improve them?
Log in to reply
The Challenge Master seems to be giving you some negative feedback. Maybe adjusting them would be a good thing.
Log in to reply
I made the note. I'm pointing out why the diagram seems to indicate that the tetrahedron point is much lower instead. And that is because the diagram is "not accurately drawn".
Plane FG is tangent to balls C, E, and A and parallel to our view. there is an oblique plane (one of the other tetrahedral encasement surfaces) touching the balls A, B, D (and a ball behind C) That oblique plane must also intersect point G because of the necessary symmetry of the solution -- point G should be the same for all three encasing surfaces. Therefore, there must exist a line in that oblique plane, that runs from G to a point tangent to ball B (the tangent point would project somewhere inside the circle of B. The line in the plane would still project as a line in our view.
I have great difficulty imagining such a line that makes sense with the necessary tangent points on A and D. It must go through G and I feel point where the line is tangent ball B would project somewhere close to but ENE of the center of B as we view it in the diagram. If I draw such a line, then I don't see realistic tangent points on Balls A and D.
Log in to reply
I have updated the image for the final solution to show where the line you are speaking of is located. While the oblique plane you mention, and its twin behind, is tangent to the spheres centered at A, D, and B, the line where it intersects its twin, that is the edge of the encasing tetrahedron, is not tangent to those spheres. This is precisely because the planes are oblique, not perpendicular to our view as is the plane tangent to spheres centered at A and C. It is because the angle between adjacent faces of a tetrahedron is so small that this distance is so surprisingly large. That is what makes the result appear so unlikely to our eyes.
@Marta Reece , I realized the solution to my problem imagining the oblique plane that intersects point G and the tangent points on balls A, B, and the ball either behind or in front of C. There is such a plane such that the points of tangency and G are on the plane. But the LINE that is defined by the points of tangency to A & B or A & C does NOT intersect G. Instead, the is a line (in the encasing plane) that runs through G, a point of tangency on A, and a point of tangency on the middle ball on the base layer, projected visually between C and B.
Consider that the spheres all fit perfectly into the tetrahedron, the edges touching.
It is reasonable to say, then, that every time you go down a layer, another layer's worth of spheres may fit exactly inside the tetrahedron.
Similarly, we can conclude that every time you go up a layer, one less layer's worth of spheres may fit exactly inside the tetrahedron.
So, from the top level with 1 sphere to an imaginary level with 0 spheres, the same vertical distance is traveled as from level 1 to level 2.
Additionally, this distance is half the distance from level 1 to level 3.
We notice that level 3 is just level 1 with a sphere added onto the side, (from the face closest to the tetrahedron). The slope between levels 3 and 1, therefore, is exactly 2 sides-of-spheres sideways to 1 sphere-heights up.
The use of different units here is because the spheres are aligned in such a way that the distances are not the same. However, it will cancel out later so it doesn't matter.
We then use this rate of 1 sphere-height/ 2 sphere-sides from the top of the level 1 sphere to the top of the nonexistant level 0 sphere, but because we only need to go half a sphere-side towards the center, (both edges are converging) we can say that the tip of the pyramid is exactly 1 sphere-height higher than the top of the sphere.
Actually the "slope between levels 3 and 1" is not "exactly 2 units sideways to 1 unit up." The slope of the side of a tetrahedron is tan ( arccos ( 3 1 ) ) = 2 2 . And there are no spheres directly below each other in levels 1 and 3.
The "level 0 sphere" does not work out because it is a continuation of the pattern of the spheres below. To be able to fit, it had to fail to continue that pattern.
Log in to reply
Ah, you're right. What I mean is it's two side-sphere-units sideways to one up-sphere-unit up. I will edit my solution to reflect that.
Since they are fit differently on the horizontal and vertical lines of sight, they aren't the same length, which is what my solution implies. What I am trying to do is use two units I don't know, but because it is all relative, it doesn't matter.
I'm not positive if this 'math' is really a viable way of explaining it, but I think it is, and if it is, then it's a very nice solution.
Log in to reply
I tried very hard to understand you, but have to admit that I failed to do so. In any event, I am convinced that you are not actually providing a solution.
Log in to reply
@Marta Reece – I agree with Marta. The 3-D configuration here is crucial to the problem, and it's independent of "travelling up a layer".
Firstly, note that when you travel up a layer, the gain in height isn't one full sphere, because the spheres are nested / sit in the gaps.
Secondly, such an arugment doesn't apply to other dimensions, or to other such configurations (like a square based pyramid). For example, in the 2-D analog, the highest point of the "tetrahedon" is much lower. Whereas, in 4-D, the highest point of the tetrahedron would be much higher.
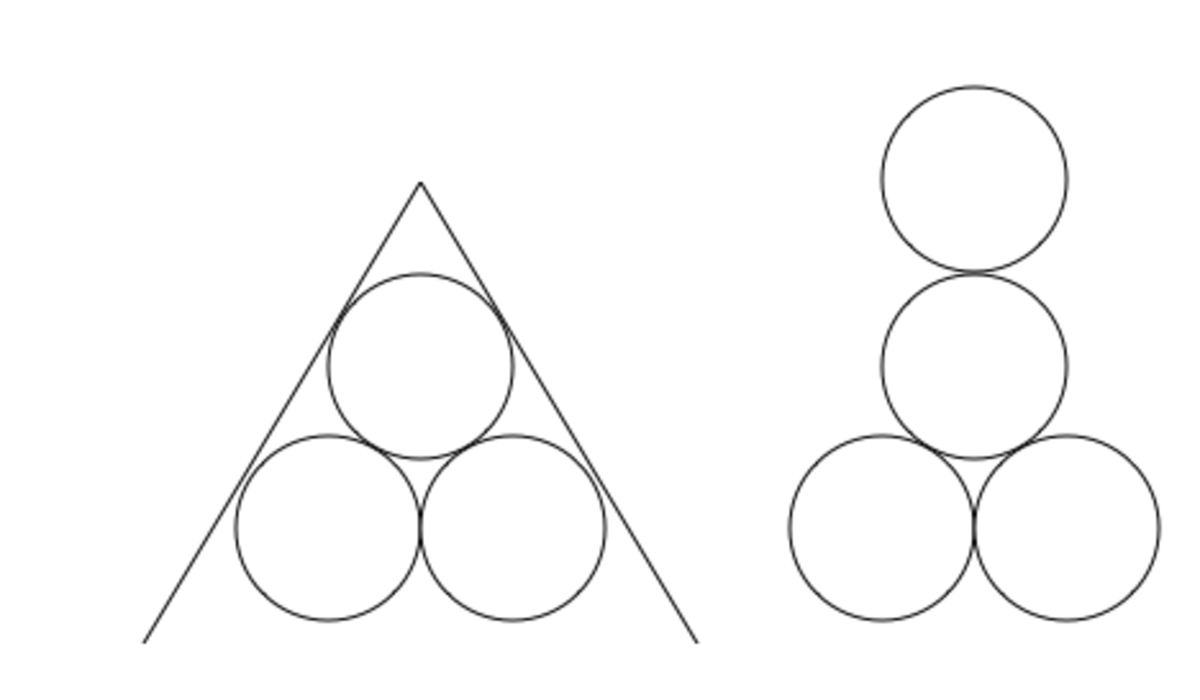
Ultimately, what is important, is accounting for the amount of vertical space from the top of the sphere to the top of the tetrahedron.
Much to my chagrin, you are correct even though I still have great difficulty visualizing it. What it really boils down to is that the distance from the center of a right tetrahedron to the center of any of its faces is exactly 1/3 the distance to any of its vertices.
Nevertheless, what you did by depicting the given case in a manner inconsistent to the problem is not exactly cricket. It's one thing to render a drawing that is not to scale. Depending on circumstance, it may or may not be necessary to give notice of that. It's something completely different to deliberately mislead the solver through the use of a drawing that incorrectly depicts the conditions of the problem, as you did. As they say, a picture is worth a thousand words. You had two pictures depicting option one inaccurately, one of them intentionally drawn to result in deception. Against that, you had nine words defining the actual condition for option 1. At the very least, you owed us 993 more words making it clear the circumstance regardless of the depiction. As the problem itself is not terribly difficult, I do believe many more of your solvers would answer this problem correctly if you simply removed the deceptive drawing.
Log in to reply
I see that you feel very strongly about this. I actually agree with you that the image is misleading and I would not be at all opposed to changing it. I did not post it; it was added by Brilliant staff to help understand the description. I will pass your opinion on and see if something can be done.
Log in to reply
@Marta Reece - Thanks for your response and for passing along my concern which seems to reinforce your original concern. The problem itself is already quite interesting in that it's difficult imagine the correctness of the answer, plus in finding the solution, it causes one to realize the geometry of the tetrahedron, and a sphere captured within, is not so easy to understand as one might expect. At least it wasn't for me. I don't think a more accurate depiction of option 1 would diminish those characteristics.
Log in to reply
@John Miller – Thanks. I see that Marta has updated the image to more accurately reflect the setup.
Sorry for the confusion.
Log in to reply
@Calvin Lin – @Calvin Lin - Thanks, that's much better. And just as I suspected, I still find it impossible to visualize the correctness of the solution.
Log in to reply
@John Miller – To be fair, I doubt it's something that could be visualized. (Much as I hate to admit it,) I think the math just happens to work out, as opposed to there being an underlying geometric interpretation.
For example, if we used a square based pyramid instead of the triangle based pyramid, then the top of the pyramid would be higher.
Log in to reply
@Calvin Lin – Ooops. Marta pointed out to me that for the square based pyramid, the top of the pyramid will actually be lower.
My misconception arose because I thought "if we're using infinitely many planes, then these planes are vertical" and so thought that going from 3 to 4 planes would make the angle more vertical (and hence a higher top).
It's an interesting visualization to understand why the top would actually be lower, or (equivalently) why the angle would be less steep.
You can derive the result from the relationship between the radii of inshere and circumsphere of a tetrahedron.
The height of the vertex of the circumscribed tetrahedron above the top sphere does not depend on the existence of the other spheres below it. It depends only on the angles typical of the tetrahedron, the fact that it is tangent to this sphere, and the sphere's radius, r . In other words the distance from the center of that sphere to the vertex is the same as if the tetrahedron enclosed only that one sphere. So we can simplify the problem to that of a single sphere inscribed in a tetrahedron. The distance from the center of this sphere (and of the tetrahedron enclosing it) to the vertex is the radius of a sphere circumscribed around a tetrahedron, R . It is known that r = 3 R , therefore the distance from the center (of the top sphere) to the vertex of the enclosing tetrahedron can accommodate exactly three radii of the sphere. This can be the radius of the original sphere plus the two radii of the additional sphere on top of it.
Or you can get the answer using only elementary geometry, namely similar triangles, Pythagorean theorem, and the formula for the area of a triangle.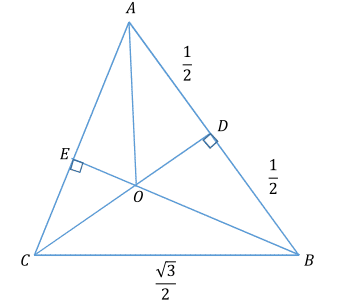 Let’s set the radius of each sphere to
4
1
. Then the centers of the ten spheres will then lay on the ends or the centers of the edges of a tetrahedron with edge equal 1. Let’s take a cross-section of it positioned so that
A
B
is an edge and
C
is located in the middle of the opposite edge. This means that
A
C
=
C
B
=
2
3
.
Let’s set the radius of each sphere to
4
1
. Then the centers of the ten spheres will then lay on the ends or the centers of the edges of a tetrahedron with edge equal 1. Let’s take a cross-section of it positioned so that
A
B
is an edge and
C
is located in the middle of the opposite edge. This means that
A
C
=
C
B
=
2
3
.
If D is the center of A B , we can get C D from the right triangle B D C as C D = B C 2 − B D 2 = 4 3 − 4 1 = 2 1 .
Area of the triangle A B C does not depend on which base and which height we pick, therefore A B × C D = A C × E B . This can be used to calculate E B = A C A B × C D = 2 3 1 × 2 1 = 3 2 .
From a right triangle C E B we can now find E C = B C 2 − E B 2 = 4 3 − 3 2 = 2 3 1 .
Triangles A D C and O E C are similar. This means E C O E = D C A D . This can be used to calculate
O E = D C A D × E C = 2 1 2 1 × 2 3 1 = 2 6 1 .
Distance O B = E B − O E = 3 2 − 2 6 1 = 2 6 3 .
So we have O A = O B = 2 6 3 and O E = 2 6 1 , or O A = 3 × O E .
All of this still applied only to the tetrahedron generated by the centers of the spheres. So to finish the calculation, we need to move out to the tetrahedron encasing the spheres, that is go outward one radius of one sphere, which we set at 4 1 , in a direction perpendicular to the face of tetrahedron.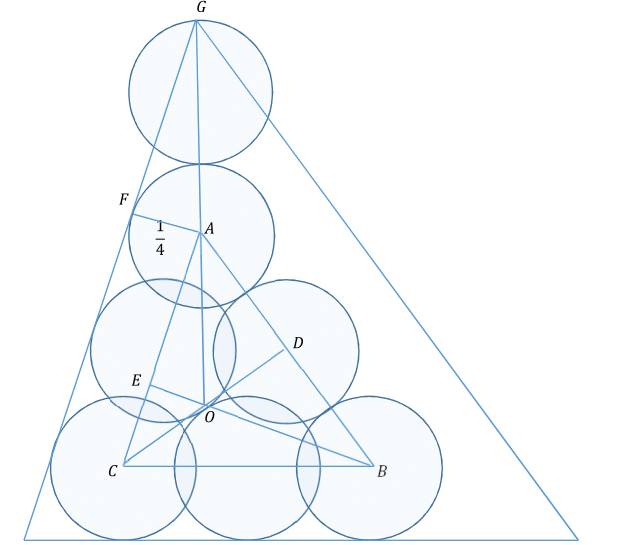 Line
A
C
is a side view of such a face. Line
A
F
is perpendicular to it. Triangle
O
E
A
is similar to triangle
A
F
G
, therefore
A
G
=
E
O
O
A
×
A
F
=
4
3
.
That is three times the radius of one of the spheres.
Line
A
C
is a side view of such a face. Line
A
F
is perpendicular to it. Triangle
O
E
A
is similar to triangle
A
F
G
, therefore
A
G
=
E
O
O
A
×
A
F
=
4
3
.
That is three times the radius of one of the spheres.