Touching circle area
Given the function, f ( x ) = x n , n ∈ R , n ≥ 2 a circle can be constructed that exactly touches, but not intersects f ( x ) . See the figure for an example.
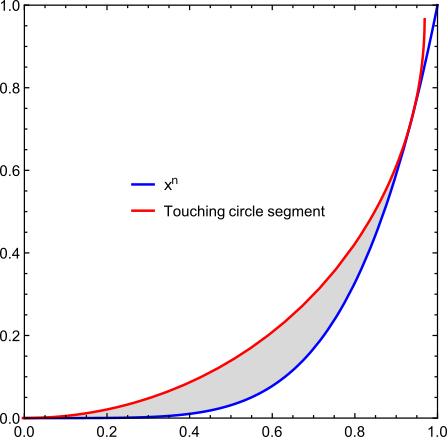
S is the area enclosed by the two curves (gray area in figure). We have n → ∞ lim S = 1 − π / 4 . What is S for n = 3 ? Give your answer to 4 decimal places.
P.S. There is a (not so nice) analytical expression for the area. Can you find it?
The answer is 0.0136001.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Now that was pretty bloody. The other way to find the point of tangency is to consider the line that is normal to the function x n and see where it intersects the y axis. From the fact that this point has to be equidistant from both the origin and a given point on that function, we can figure out where this point is. The next step is to integrate, but I don't know how to improve on the way you did it.
Log in to reply
Ah, yes, that would be a good approach. This was a tedious solution to type up; once I got to the integral I thought about just using WolframAlpha, but I know I would have been chastised by the Challenge Master for doing that. :P
Log in to reply
Maybe instead of trying to integrate the circular arc, just compute the area underneath directly by other geometrical means. Integrating x 3 is not hard, once you know the coordinates of the point of tangency.
Log in to reply
@Michael Mendrin – Oh, that's much easier. Form a rectangle with the origin as the lower left corner and ( x , r ) = ( 3 − 4 1 , 2 ∗ 3 − 4 3 ) as the upper right corner. We can then divide this rectangle into a sector of radius r with a central angle that turns out to be θ = 3 π radians, a triangle above this sector with dimensions x by 2 r , and the region below the sector. So the area of this last region is
x r − ( 2 1 ∗ 2 x r + 2 1 r 2 θ ) = 3 2 − ( 2 1 ∗ 3 1 + 2 1 ∗ 3 3 2 ∗ 3 π ) = 2 1 − 9 3 2 π .
Then, as you say, we do the straightforward integral for x 3 which comes out to 1 2 1 , and then subtract this from the above value to get the same final answer as before. So besides this one integral it's become almost a pure geometry question. Great idea. :)
I suppose the next thing would be to generalize S and θ for any n , but I think I've spent enough time on this problem for now.
It is reasonable to assume that the circle to be constructed will have one point of intersection with the given curve at the origin. The radius r circle is then described by the equation x 2 + ( y − r ) 2 = r 2 , Now for the circle to touch (but not intersect) the curve y = x 3 at a second point we require that not only do the curves pass through this point but that their tangents coincide at this point too.
Working in the first quadrant, and noting that the point of tangency P ( x , y ) will have a y -coordinate less than r , (since x 3 is an increasing function), we have that, for the circle, y = r − r 2 − x 2 . So for the two curves to meet, we require that
x 3 = r − r 2 − x 2 , (A),
and since their tangents must coincide, we also require that the derivatives are equal at P , i.e.,
3 x 2 = r 2 − x 2 x ⟹ r 2 − x 2 = 3 x 1 , (B)
where we divided through by x since we want P other than the origin. Substituting (B) into (A) gives us that
x 3 = r − 3 x 1 ⟹ r = x 3 + 3 x 1 .
Substituting this result into (A) and simplifying gives us that
3 x 1 = x 6 + 9 x 2 1 + 3 2 x 2 − x 2
⟹ 9 x 2 1 = x 6 + 9 x 2 1 + 3 2 x 2 − x 2
⟹ x 6 = 3 x 2 ⟹ x 4 = 3 1 ⟹ x = 3 − 4 1 .
This in turn gives us that r = x 3 + 3 x 1 = 2 ∗ 3 − 4 3 .
So now we just need to evaluate the integral
∫ 0 3 − 4 1 ( r − r 1 − ( r x ) 2 − x 3 ) d x ,
(where of course x is now being used as a variable). The first and third components of the integrand are straightforward and yield a value of 1 2 7 .
The second component can be evaluated using the substitution
r x = sin ( θ ) ⟹ d x = r cos ( θ ) d θ .
The integral of this component then becomes
∫ r 2 cos 2 ( θ ) d θ = 2 r 2 ( θ + sin ( θ ) cos ( θ ) ) d θ =
3 3 2 ( arcsin ( r x ) + r x 1 − ( r x ) 2 ) ,
which when evaluated from x = 0 to x = 3 − 4 1 comes out to
3 3 2 ∗ ( arcsin ( 2 3 ) + 2 3 ∗ 2 1 ) = 3 3 2 ∗ ( 3 π + 4 3 ) = 9 3 2 π + 6 1 .
Subtracting this from 1 2 7 yields a desired area value of
1 2 5 − 9 3 2 π = 0 . 0 1 3 6 0 to 4 decimal places.