Tracing an Ellipse

This is what a degenerate ellipse, a line segment, will become after being traced. The resulting sausage shape is clearly not an ellipse.

One could argue that a line segment is not an ellipse either, but there is one very close to it, with a tiny short axis, and tracing it will result in a very sausage-line shape, that is a shape with curvature practically zero for a large distance, much larger and close to constant for a time, then again close to zero, and again almost constant. Not a behavior of an ellipse.

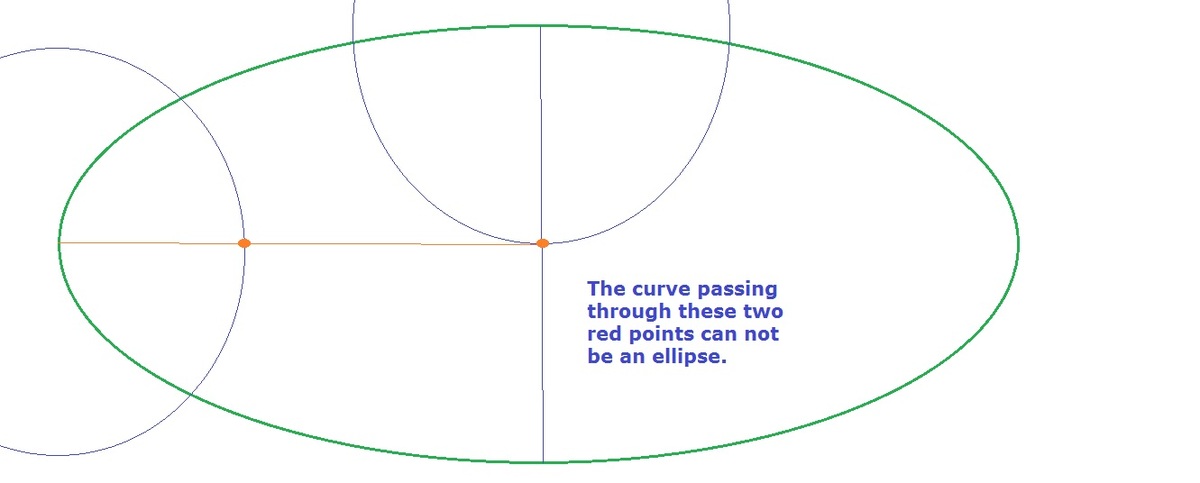
Well we can take extreme example. The radius of the pen circle is =length of minor axes. Then the point on inner curve when the pen center is at end of minor axis, is at the center, that is one end of major axes.
When the pen center is at end of major axis, again the point on the inner curve is on the major axis.
Thus the inner curve pass through the two points of the Major axes while the pen traces a quater ellipse. Not what happens to an ellipse.

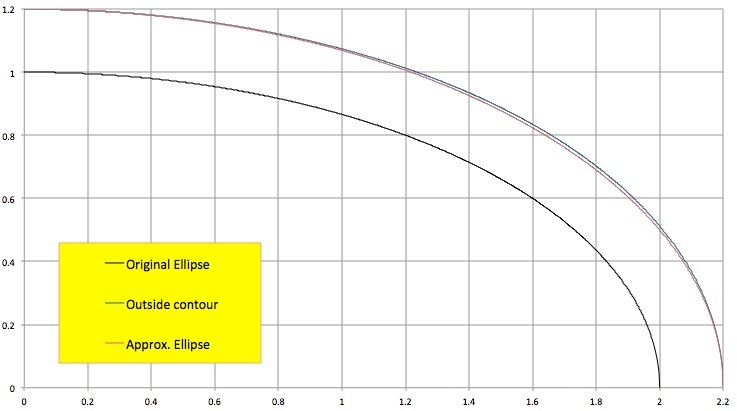
The following graph shows a quarter ellipse with semi-major axis 2 and semi-minor axis 1. The blue curve is the outside border of a trace with a circular nib of radius 0.2. The red curve is the orthogonal ellipse matching the blue curve in the points $(2.2,0)$ and $(0,1.2)$ . The red and blue curve do not coincide, showing that the blue curve is not an ellipse.

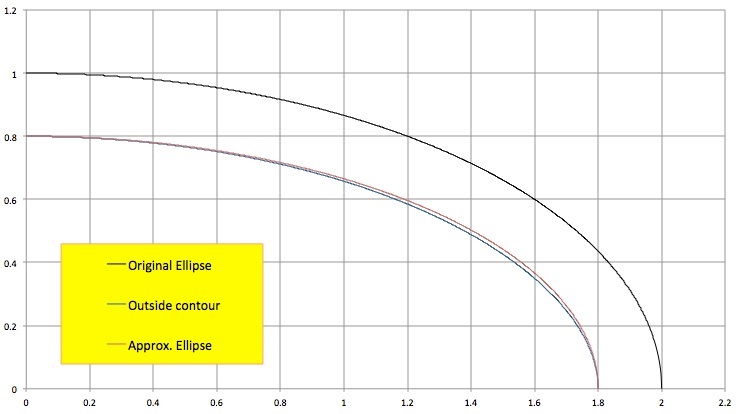
And here is the same graph for the inside border:

The graphs were generated as follows. First, an orthogonal ellipse is defined by an equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1;$ I chose $a = 2$ and $b = 1$ . Now determine the direction perpendicular to the ellipse at a point $(x,y)$ : $\vec n \propto \left(\frac{x}{a^2},\frac{y}{b^2}\right).$ The length of this vector is $\sqrt{x^2/a^4 + y^2/b^4}$ , but we want a vector of length $r$ (the nib radius). Thus we scale $\vec n$ . Finally, add it to the original position $(x,y)$ to find the point on the boundary: $(x',y') = \left(x + \frac{rx/a^2}{\sqrt{x^2/a^4 + y^2/b^4}}, y + \frac{ry/b^2}{\sqrt{x^2/a^4 + y^2/b^4}}\right).$

It might be more elegant to prove that the curve defined by $(x',y')$ does not obey the equation of an ellipse; but the algebra is rather nasty!

The general form of an ellipse is $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$ .

If we consider the inner border one, it must have smaller axes. Let's mark the difference with $\Delta$ , which results in the following equation: $\frac{x^2}{(a-\Delta_1)^2}+\frac{y^2}{(b-\Delta_2)^2}=1$

From there, it is easy to see that there is always some $\Delta_1$ and $\Delta_2$ for which the equation becomes undefined and unsolvable. This means that the equation is not a good description for all inner borders and therefore the inner border for any ellipse is not an ellipse.

Take an ellipse with minor semi-axis length equal to the radius of the circle. Then the inner blue path will cross itself at the center of the ellipse. This path cannot be an ellipse.

If we have two ellipses one with a value of A to be a and the other (a+1), and B to be b and (b+1) as we assume the pen has a radius of 1, now if we expand the equation of an ellipse and differentiate, we see that the gradient function of the two ellipses are different so they will not be borders to each other as they must have the same gradient function, in a circle to change the radius you have to add a constant to the end of the equation i.e. like $(x+3)^2 + (y-3)^2 = r^2$ all we have to do is add to the $r^2$ side, and as $\frac{d}{dx}(r^2) = \frac{d}{dx}(r^2 + k)$ where k is a constant, however in the case of an ellipse $b^2 x^2 + a^2 y^2 = a^2 b^2$ which becomes $b^2x^2 +2bx^2+ x^2 + a^2y^2 + 2ay^2 + y^2 = a^2b^2$ when $a = a+1$ and $b = b + 1$ , it can easily be seen that the derivatives of these two equations are not equal.

Since an eclipse is different than a circle, the lines would cross each other, letting there be no eclipses forming, correct me if I'm wrong.