Tracing paths
Inspired by this daily problem , and as in it, we have the following figure, that is to be traced without lifting your pencil or adding anything.
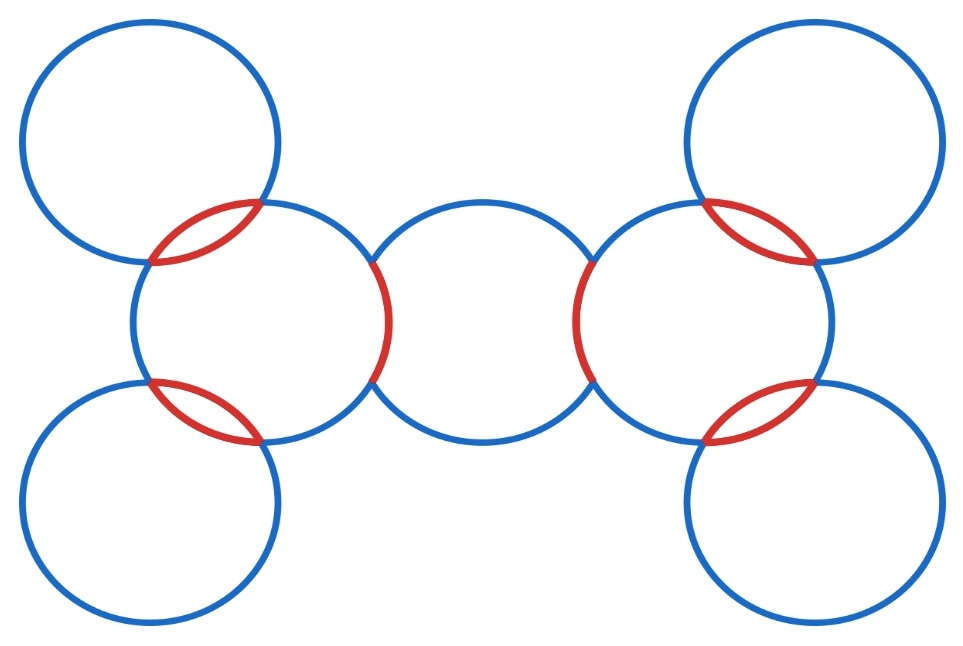
The combined length of all the lines in this figure is 40, each circle has a circumference of 6 and each red arc has a length of 1. You have to trace the whole figure and not add anything to it. What is the minimum length of arc must be traced over more than once to achieve this?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Viewing the diagram as a road map, there are 4 intersections with 3 roads leading out (near the center), and 8 intersections with 4 roads leading out (near the edges).
With the exception of the starting and ending points, a continuously traced path can only go through intersections with an even number of roads leading out, because half the roads at the intersection must be used to approach the intersection and the other half must be used to leave. The intersections with an odd number of roads leading out can only be used for 2 points, the starting and ending points, but in this diagram there are 4. Therefore, it is not possible to trace the whole diagram without lifting your pencil or covering the same line twice.
However, starting at point S and ending at point F, the following path can be traced out, which only overlaps one red arc near the middle, showing that the next minimum arc length choice of 1 is possible.