Trajectory Evaluation
A particle is launched at time t = 0 from ground level with initial speed v 0 at an angle θ with respect to ground. Gravitational acceleration g is downward.
Let T ( t ) be the particle's kinetic energy as a function of time, and let V ( t ) be the particle's gravitational potential energy as a function of time, measured with respect to ground. Let t f be the time at which the particle lands.
If θ = 4 5 degrees, what is the following ratio?
∫ 0 t f V ( t ) d t ∫ 0 t f T ( t ) d t = ?
The answer is 2.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
@Krishna Karthik
Thank you so much sir for this solution.
I just upvoted
Log in to reply
You're welcome bro, cheers!
Woah I just found a really weird brilliant glitch... You can actually get the "interesting" option into the negatives such as negative 5 and stuff by just repeatedly clicking lol
Log in to reply
@Krishna Karthik
yes, nice catch.
But i think after some time it will come to it's original values.
I don't know why but Helpful option is not going into negative. Ha ha
Log in to reply
@A Former Brilliant Member – Yeah; if you refresh the browser it's simply all increment by only one. Kinda funny though lol🤣
Log in to reply
@Krishna Karthik – @Krishna Karthik think logical if confused option is in negative then it means, that the person agrees with the solution.
Log in to reply
@A Former Brilliant Member – Lol, that's a funny way to interpret a bug. If the interesting option is negative then that's kinda sad🤣 If the brilliant option is negative then someone is trying to call the solution writer dumb LMAO🤣
Log in to reply
@Krishna Karthik
–
@Krishna Karthik
do you play chess?
If yes, we can play chess together at chess.com
Log in to reply
@A Former Brilliant Member – Yes, I certainly play chess. Let's play at chess.com!
Log in to reply
@Krishna Karthik – @Krishna Karthik please give me your username
Log in to reply
@A Former Brilliant Member – It's Kk1356
Log in to reply
@Krishna Karthik – @Krishna Karthik request sent
Log in to reply
@A Former Brilliant Member – Yup, I accepted. Let's play!
Python code based solution:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
|
@Karan Chatrath sir thank you so much ,i was struggling for this (i just upvoted)
btw how can i plot
α
=
2
sin
2
θ
3
−
1
this in excel.
if i plot that curve in my solution it will be awesome .
thanks in advance
Log in to reply
This is a pretty straightforward operation in Excel. Refer to the internet to see how to plot a any function y = f ( x ) using Excel. The explanation would be detailed but the steps are simple.
Nice one. One could also run while y ≥ = 0 , eliminating the need to calculate the final time.
Log in to reply
@Steven Chase
sir for this problem only?
if we do
y
>
=
0
we don't have to calculate time???
is this you want to say
Log in to reply
If you use the "while" loop, you don't need to pre-calculate the final time
Log in to reply
@Steven Chase
–
@Steven Chase
sir i did not understand much,i will be happy if you post the solution of this problem only by the method of python without calculating time.
thanks in advance.
Yes, in hindsight, choosing y as the loop variable is a better way of solving the problem. I have edited my solution. Thanks for the feedback.
Log in to reply
Yes, very true. Calculating the time required is an unnecessary condition if you know it'll land at y = 0 .
@Steven Chase ohhh after seeing the edited solution i can feel what Steven sir wants to say 1 hour ago.
@Karan Chatrath
sir how can we make 2D images in python representing 3D things.
Suggest me some website or video to learn.
Thanks in advance.
Log in to reply
By images, do you mean plots?
Log in to reply
@Karan Chatrath
Yes sir like this problem have https://brilliant.org/problems/more-paraboloid-surface-dynamics/
I also want to post question like this images
I like this types of images very much.
How can I learn to make this images?
Thanks in advance.
Log in to reply
@A Former Brilliant Member – You can write a code on python generating the coordinates of that surface and then you can export it to excel and generate a 3D plot. I am not sure how to export data from python to Excel but I am sure it is possible.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
can you give me 1 code , no matter whatever the plot in 3D you are giving me.
I know how to export it to excel.
But I don't know how to write this code in python.
If you give me one code it will be a good example for me , to how to draw
We can check.
Thanks in advance.
Log in to reply
@A Former Brilliant Member – Okay, I will do that. I do not know how to export data from Python to excel, so I am hoping you will help me with that. That way we both learn something new. Sounds good?
I will type and code and share it after some time.
Log in to reply
@Karan Chatrath – @Karan Chatrath Fine sir!
Log in to reply
@A Former Brilliant Member – Actually, can you tell me how to export data from python to excel? I will attach the code shortly
Log in to reply
@Karan Chatrath – That opaque helix is one example. But there are much simpler examples
Unit hemisphere centered at the origin. The data is exported to 'HEM.txt'. Copy that to Excel and try 3D plotting the vectors.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
|
Log in to reply
@Neeraj Anand Badgujar Hope this is helpful.
Log in to reply
@Karan Chatrath
I am getting this
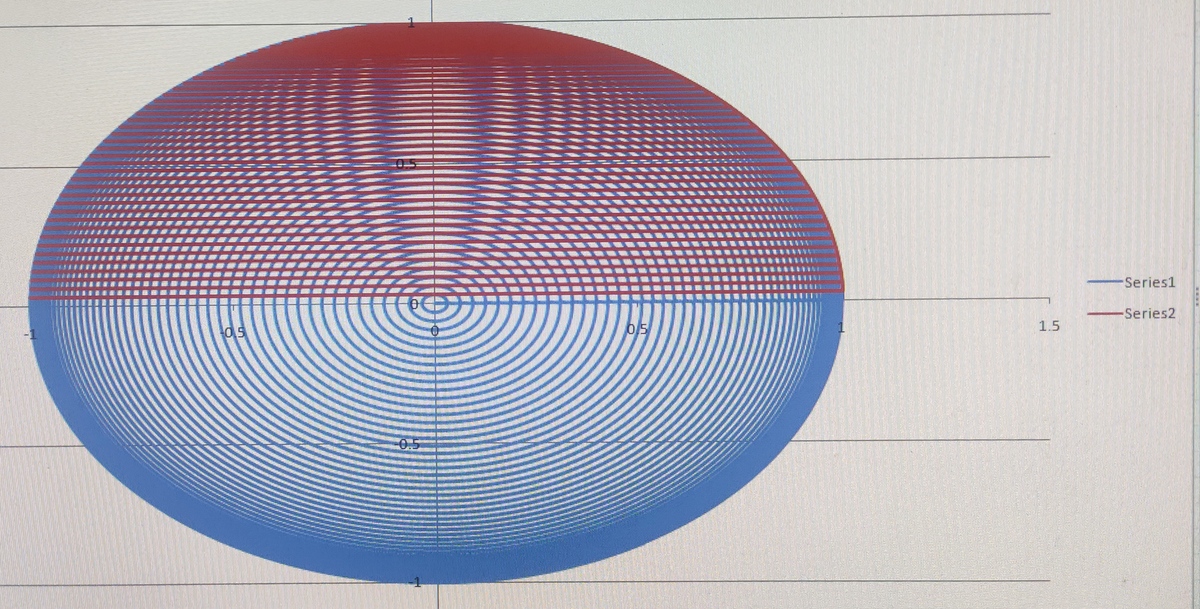
Log in to reply
@A Former Brilliant Member – Yes, that is not a 3D plot. How to generate 3D plots in Excel is something I am unsure of at this moment. But the code I provided does generate the required data.
Maybe @Steven Chase can provide some insight into this.
Some context: This is an unsuccessful attempt at plotting a unit hemisphere centred at the origin, as a 3D surface.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
sir i think Steven sir is sleeping now .
Hope he will give us a reply in 3-4 hours .
@Karan Chatrath
–
@Karan Chatrath
sorry sir . You have done your work from your side is perfect but i failed for my contribution.
but i am trying that how to make 3-D plots from web
Log in to reply
@A Former Brilliant Member – Oh, no worries. 3D plots on Excel are tricky. I couldn't figure this out myself and am curious to learn about it. I will continue to try searching for an answer later on.
Log in to reply
@Karan Chatrath – @Karan Chatrath can we make in MATLAB??
Log in to reply
Log in to reply
@Karan Chatrath – @Karan Chatrath wow it's very Beautifull
@Karan Chatrath – Regarding 3D plots in Excel, as I do them, Excel is very dumb. It just plots points. The code script is where all the brains are.
Log in to reply
@Steven Chase
–
@Steven Chase i laughed so hard when i read that "Excel is very dumb"
sir according to you which tool is best for making 3-D plots except tools like MATLAB which are very expensive??
Log in to reply
@A Former Brilliant Member – There is an add-on pack for Python called sci-py that has all kinds of extra features like plotting. That might be something to look at.
Log in to reply
@Steven Chase
–
@Steven Chase
How can i install it in my computer ??
Did u have installed??
From this
Problem
we know that the generalise value of
∫
0
t
f
V
(
t
)
d
t
∫
0
t
f
T
(
t
)
d
t
=
α
comes out to be
3
2
sin
3
θ
sin
θ
+
3
4
sin
3
θ
−
2
sin
3
θ
=
α
simpifying the
α
leads to
α
=
2
sin
2
θ
3
−
1
Now ,lets put
θ
=
4
5
degrees
α
=
2
I will be happy if anyone will post the solution of this problem by solving it with python programming.
Thanks in advance
Log in to reply
Just solved this problem. I have posted a python based solution.
We can show (see this ) that the ratio is
η = 2 sin 2 θ 3 − 1
Here θ = 4 5 °
So η = 2 × 2 1 3 − 1 = 3 − 1 = 2 .
Here's a python solution.
Neeraj, what I have done here in the code is as follows:
First step: Set the condition to when the object hits the ground, when y > = 0 .
Second step: Calculate the Kinetic and Potential energy of the object during trajectory by finding magnitude of velocity and dividing by 2, and potential by finding m g h .
Third: Increment the value of x every 1 0 − 7 seconds. This will be done by multiplying the time by the velocity, does adding small distances to the current distance. On a more technical perspective this is called Euler Integration.
4rth: Do the same steps to the y value, by calculating velocity using the acceleration and then numerically integrating to get the displacement.
5th: using the computations, numerically integrate to find the integrals of the Kinetic and Potential Energy.