Transformer Exercise (Part 2)
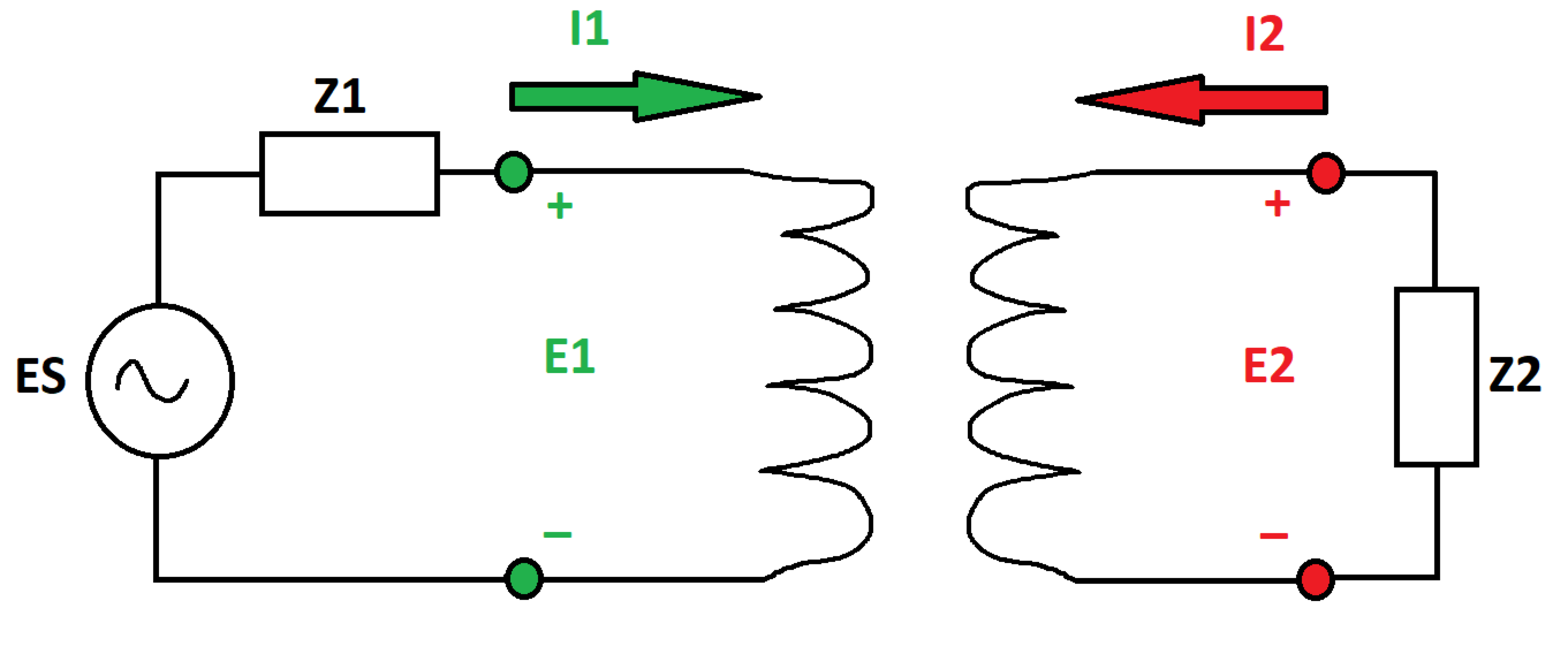
A particular transformer is governed by the following equations:
E 1 = Z S I 1 + Z M I 2 E 2 = Z M I 1 + Z S I 2
In the equations, E 1 and E 2 are the terminal voltages and I 1 and I 2 are the terminal currents (note the polarity conventions in the diagram). Z S and Z M are the transformer self and mutual impedances.
An AC voltage source with internal voltage E S and internal impedance Z 1 is connected across the first set of terminals, and an impedance Z 2 is connected across the second set of terminals.
What is the magnitude of E 2 ?
Details and Assumptions:
1)
E
S
=
0
+
j
1
0
2)
Z
1
=
2
+
j
5
3)
Z
2
=
5
+
j
5
4)
Z
S
=
0
+
j
1
0
5)
Z
M
=
0
+
j
5
6)
Consider all quantities to be complex numbers. The quantity
j
is the imaginary unit
The answer is 1.629.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Steven Chase
I am enjoying this series very much. Please continue it for part 3
Thanks in advance
@Steven Chase sir I have uploaded a new problem.
@Steven Chase Sir why didn't you give a reply that you have seen the new problem or not??
Log in to reply
That's a pretty interesting problem. I have attempted it, but my answer was not accepted
Log in to reply
@Steven Chase
sir whenever I dedicate a problem I try to make hard as possible as I can. Maybe the solution which I have solved, there would be some error, it take me whole 1 day to do that calculations.
Can you share what answer you are getting,
I will check my solution later.
Log in to reply
@A Former Brilliant Member – Let me also check my work again, and when I am sure that it is the best I can do, I will share it. Thanks
Referring to the system of equations derived by @Steven Chase , the final equation to compute the absolute value of E 2 can be re-arranged in a matrix form to be:
∣ E 2 ∣ = m o d ( [ Z M Z S ] [ Z 1 + Z S Z M Z M Z 2 + Z S ] − 1 [ E S 0 ] )
This is effectively only one line of MATLAB code, excluding initialisations.
1 |
|
@Karan Chatrath
It concludes that MATLAB is very strong
Right??
BTW sir i have studied Laplace very well.
Now I am able to solve 2nd order differential equation.
Please can you upload a problem ??
I will upload solution using Laplace.
Thanks in advance.
Nice problem.
The basic equations are
E
1
=
Z
s
I
1
+
Z
M
I
2
E
1
=
j
(
1
0
I
1
+
5
I
2
)
E
2
=
Z
M
I
1
+
Z
s
I
2
E
2
=
j
(
5
I
1
+
1
0
I
2
)
Using Kirchoff's voltage rule
E
s
−
I
1
Z
1
=
E
1
E
2
=
−
I
2
Z
2
Solving the above
2
equation for
I
1
and
I
2
gives
I
2
=
3
7
7
7
6
+
3
7
7
4
2
j
E
2
=
−
I
2
Z
2
Substituting the values of
Z
2
and
I
2
in the above equation, and taking it's modulus gives
∣
E
2
∣
≈
1
.
6
2
8
Sir please post more problems like this one and upgrade them also.
Thanks for this
I am expecting a MATLAB solution from @Karan Chatrath Sir.
Thanks in advance.
Log in to reply
I solved it the same way as @Steven Chase did, by using linear algebra.
@Neeraj Anand Badgujar has shown how the solution works. I will post some Python code which uses the linear system solver to calculate the currents. I will re-iterate the equations for the sake of completeness.
Basic equations
E 1 = Z S I 1 + Z M I 2 E 2 = Z M I 1 + Z S I 2
Substituting in for E 1 and E 2 :
E S − Z 1 I 1 = Z S I 1 + Z M I 2 − Z 2 I 2 = Z M I 1 + Z S I 2
Consolidating terms:
E S = ( Z S + Z 1 ) I 1 + Z M I 2 0 = Z M I 1 + ( Z S + Z 2 ) I 2
Solve the linear system for the currents. Then calculate the terminal voltages.