Transformer Exercise (Part 3)
Two transformers are placed in series. The transformers obey the following equations:
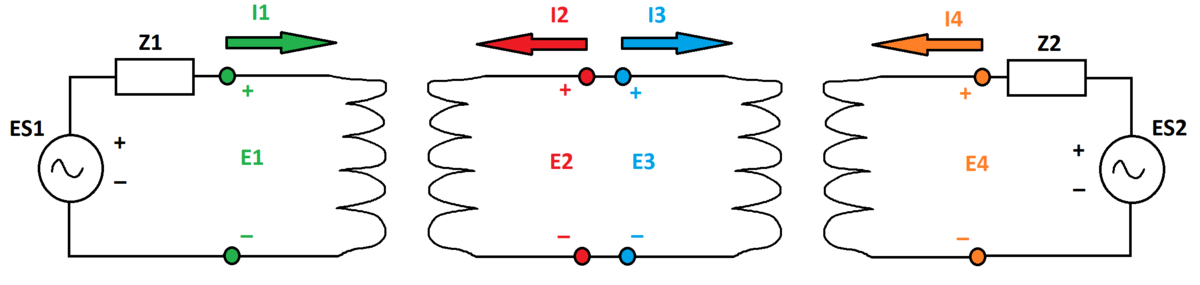
E 1 = Z S 1 I 1 + Z M 1 I 2 E 2 = Z M 1 I 1 + Z S 1 I 2 E 3 = Z S 2 I 3 + Z M 2 I 4 E 4 = Z M 2 I 3 + Z S 2 I 4
In the equations, E 1 , E 2 , E 3 , and E 4 are the terminal voltages and I 1 , I 2 , I 3 , and I 4 are the terminal currents (note the polarity conventions in the diagram). Z S 1 and Z M 1 are the self and mutual impedances for the first transformer, and Z S 2 and Z M 2 are the self and mutual impedances for the second transformer.
An AC voltage source with internal voltage E S 1 and internal impedance Z 1 supplies the transformers on one side, and an AC voltage source with internal voltage E S 2 and internal impedance Z 2 supplies the transformers on the other side.
A certain amount of active power enters the left terminals of the first transformer. Since the transformers have no resistance, the same amount of active power exits the right terminals of the second transformer.
How much active power is transferred through the transformers?
Details and Assumptions:
1)
E
S
1
=
1
0
+
j
3
2)
E
S
2
=
1
0
+
j
0
3)
Z
1
=
3
+
j
3
4)
Z
2
=
2
+
j
1
5)
Z
S
1
=
0
+
j
4
6)
Z
M
1
=
0
+
j
2
7)
Z
S
2
=
0
+
j
6
8)
Z
M
2
=
0
+
j
2
9)
Consider all quantities to be complex numbers. The quantity
j
is the imaginary unit
10)
This article
explains what active power is
The answer is 0.3391.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Steven Chase Sir thanks for posting, I have learned something new :)
Great problem as always. Thanks for posting. The circuit equations as per Kirchoff's voltage law are:
− E S 1 + I 1 Z 1 + E 1 = 0 − E 2 + E 3 = 0 − E 4 − I 4 Z 2 + E S 2 = 0
According to Kirchoff's current law for the second loop:
I 2 + I 3 = 0
Rearranging these four equations in a matrix form:
⎣ ⎢ ⎢ ⎡ Z 1 + Z S 1 − Z M 1 0 0 Z M 1 − Z S 1 0 1 0 Z S 2 Z M 2 1 0 Z M 2 Z S 2 + Z 2 0 ⎦ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎡ I 1 I 2 I 3 I 4 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ E S 1 0 E S 2 0 ⎦ ⎥ ⎥ ⎤ ⟹ ⎣ ⎢ ⎢ ⎡ I 1 I 2 I 3 I 4 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ Z 1 + Z S 1 − Z M 1 0 0 Z M 1 − Z S 1 0 1 0 Z S 2 Z M 2 1 0 Z M 2 Z S 2 + Z 2 0 ⎦ ⎥ ⎥ ⎤ − 1 ⎣ ⎢ ⎢ ⎡ E S 1 0 E S 2 0 ⎦ ⎥ ⎥ ⎤
The active power is the real part of the product of the current through the terminal and the terminal voltage:
P a = r e a l ( E 1 I 1 ∗ )
Here, I 1 ∗ is the complex conjugate of current. The required answer evaluates to: P a ≈ 0 . 3 3 9 1
Thanks for the solution. Did you check the other side too?
Log in to reply
Yes, that is how I confirmed that my answer is correct. I was initially computing the power without taking complex conjugates. This check was a helpful hint in the problem statement.
The absolute value of the real parts of the power at each end are equal.
Log in to reply
@Karan Chatrath
Sir I have also uploaded my solution .
And I am waiting for your RLC problem in which I will post solution through Laplace
Thanks in advance.
@Steven Chase You have added Note, especially to clear my doubt. Smart
Log in to reply
Yes, it's a one-dimensional problem, and it starts at y = 0
Very nice problem.
The basic 8 equations are: E 1 = ( 0 + j 4 ) I 1 + ( 0 + j 2 ) I 2 E 2 = ( 0 + j 2 ) I 1 + ( 0 + j 4 ) I 2 E 3 = ( 0 + j 6 ) I 3 + ( 0 + j 2 ) I 4 E 4 = ( 0 + j 2 ) I 3 + ( 0 + j 6 ) I 4 E S 1 − I 1 Z 1 = E 1 I 2 = − I 3 E 2 = E 3 E S 2 − I 4 Z 2 = E 4
Solving this 8 simple equations gives I 1 = 5 6 5 4 5 0 8 3 − j 5 6 5 4 5 7 9 5 I 2 = 5 6 5 4 − 6 1 7 − j 5 1 4 3 3 I 3 = 5 6 5 4 6 1 7 + j 5 1 4 3 3 I 4 = 2 8 2 7 9 9 9 − j 2 8 2 7 3 8 0 5 E 1 = 2 8 2 7 1 1 9 5 3 + j 2 8 2 7 9 5 4 9 E 2 = 2 8 2 7 6 5 2 1 + j 2 8 2 7 3 8 4 9 E 3 = 2 8 2 7 6 5 2 1 + j 2 8 2 7 3 8 4 9 E 4 = 2 8 2 7 2 2 4 6 7 + j 2 5 7 6 0 1
Now the read the 7 t h and 8 t h line of the problem carefully.
To calculate active power , we only calculate the real part of P a c t i v e = E 1 I 1 ˉ
Where the bar line over the I 1 ˉ tells the complex conjugate of I 1
Suppose we take take a complex number N = x + j y
Then it's complex conjugate is N ˉ = x − j y
Now come to the problem P a c t i v e = ( 2 8 2 7 1 1 9 5 3 + j 2 8 2 7 9 5 4 9 ) ( 5 6 5 4 5 0 8 3 + j 5 6 5 4 5 7 9 5 ) P a c t i v e ≈ 0 . 3 3 9 1 3 2 4 + j 7 . 3 7 0 2 6 0 8
Our job is to take real part only P a c t i v e ≈ 0 . 3 3 9 1 3 2 4