Transformer Exercise
A particular transformer is governed by the following equations:
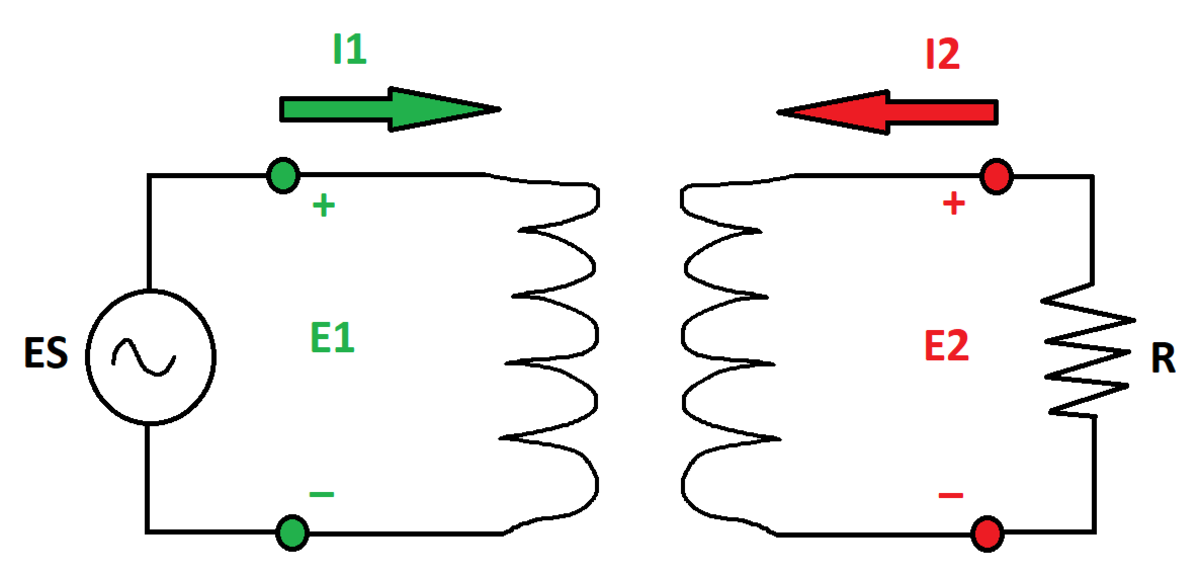
E 1 = Z S I 1 + Z M I 2 E 2 = Z M I 1 + Z S I 2
In the equations, E 1 and E 2 are the terminal voltages and I 1 and I 2 are the terminal currents (note the polarity conventions in the diagram). Z S and Z M are the transformer self and mutual impedances.
An ideal AC voltage source E S is connected across the first set of terminals, and a resistor R is connected across the second set of terminals.
What is the magnitude of E 2 ?
Details and Assumptions:
1)
E
S
=
1
0
2)
R
=
1
0
3)
Z
S
=
j
1
0
4)
Z
M
=
j
5
5)
Consider all quantities to be complex numbers. The quantity
j
is the imaginary unit
Bonus: What happens with ( Z S , Z M ) = ( j 1 , j 0 . 5 ) or ( Z S , Z M ) = ( j 0 . 1 , j 0 . 0 5 ) ? How can this be interpreted?
The answer is 4.0.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Thanks for looking at the bonus. Yes, the key takeaway is that the transformer given is not an ideal transformer. It can be represented as a series impedance, known as a "leakage impedance", in series with an ideal transformer. And then your comment about the convergence applies.
Log in to reply
@Steven Chase
sir i am not able to make a very hard question therefore the dedication problem will take some more time
BTW how can we solve this problem
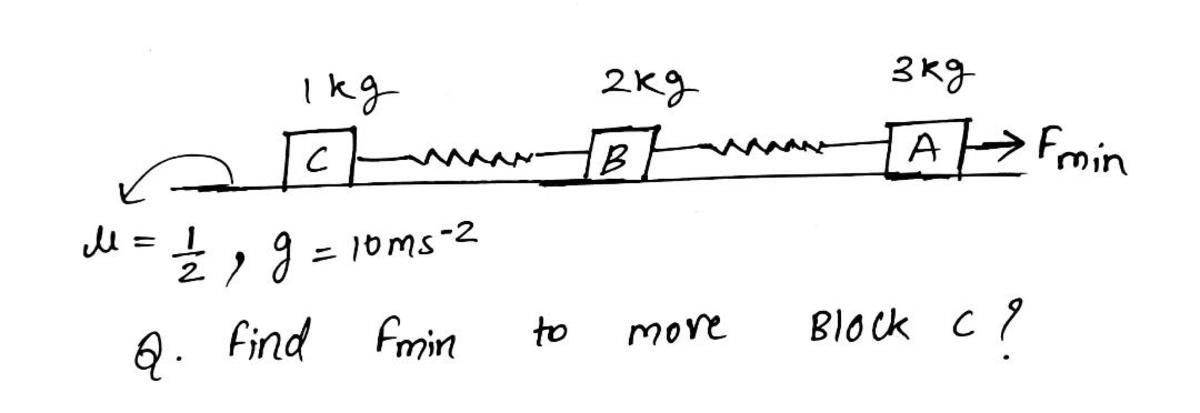
Analytically, as the two block was solved, That one was very easy to deal. But this time it is getting hard for me.
@Karan Chatrath
sir i also want you to join our discussion.
@Steven Chase sir when did you uploaded part 2 , is it now?
Log in to reply
Yes, just a minute ago
Log in to reply
@Steven Chase
–
@Steven Chase
I was just roaming here and there.
Suddenly I noticed part 2 is written there.And I am trying it now.
Anyway, Good Morning.
@Karan Chatrath
Sir for your new problem I have solved it but with Laplace, I am not getting answer,
Below i have attached my attempt.
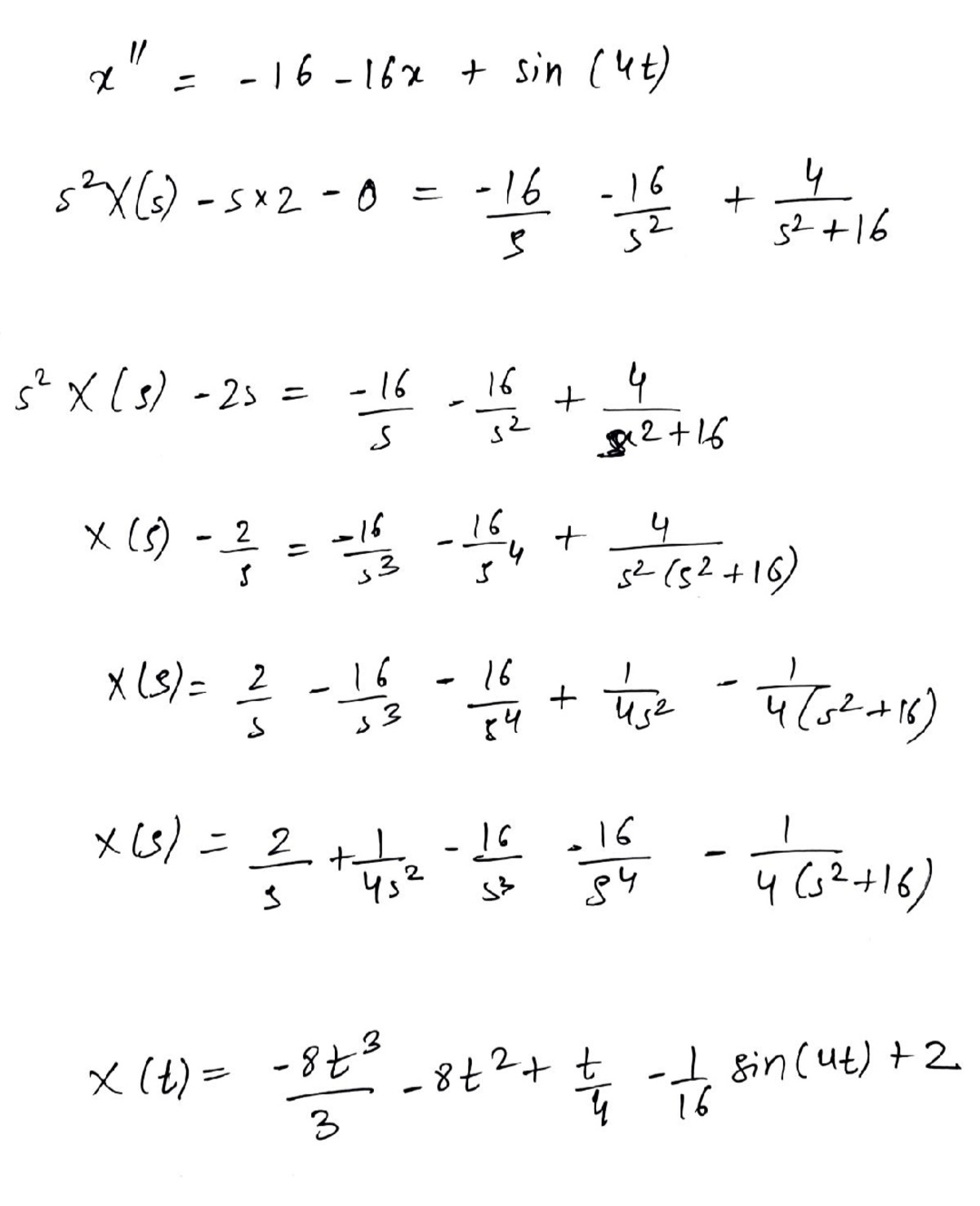
Thanks in advance
Log in to reply
The equation of motion is incorrect. The step where you take Laplace transform on both sides is also incorrect.
Log in to reply
Method of undetermined coefficients should suffice, I suppose. Or my personal favorite; numerical integration
Log in to reply
@Steven Chase
–
@Steven Chase
Hii,
Can we start some new exercise like transformer???
@Karan Chatrath sir is the first equation correct??
Log in to reply
@A Former Brilliant Member – No, there is a tiny error there.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
i don't think because I have solved that differential equations and solved your problem correctly in after 1hr after you upload.
But I want Laplace.
Please correct me if I am wrong
Log in to reply
@A Former Brilliant Member – You wrote:
x ¨ = − 1 6 − 1 6 x + sin ( 4 t )
Whereas the correct equation should be:
x ¨ = 1 6 − 1 6 x + sin ( 4 t ) Take laplace transform on both sides:
s 2 X − 2 s = s 1 6 − 1 6 X + 1 6 + s 2 4 X = s 2 + 1 6 s 1 6 + 1 6 + s 2 4 + 2 s
And proceed...
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
sir I am getting
-
sign on that 16 also.
Ok wait let me share my approach.
@Karan Chatrath
consider 2nd page as 1st page.
And 1st page as second page
Log in to reply
Your first equation is definitely wrong. Look up the definition of spring force. The equation for total energy is also incorrect. As for getting the correct answer, I think you got lucky here.
E = 2 1 k x 2
Log in to reply
@Karan Chatrath
BTW I am a very unlucky guy
So what is the equation of energy????
Log in to reply
@A Former Brilliant Member – E = 2 1 M x ˙ 2 + 2 1 K ( x − L o ) 2
Log in to reply
@Karan Chatrath – @Karan Chatrath i was getting x ˙ = 0 at that time.
Log in to reply
@A Former Brilliant Member – If x ˙ = 0 , then x = c o n s t a n t . The particle stays at rest throughout time. That is not true. Try to physically interpret the results of any mathematical evaluation. That would be a useful quality to develop.
Log in to reply
@Karan Chatrath – @Karan Chatrath sir according to your calculations, what velocity of block you are getting at t = 2 9 π
Log in to reply
@A Former Brilliant Member – Okay, I see your point. I realised that I misunderstood your previous comment. The velocity at that instant is indeed zero. However, your expression for PE was still not okay.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
But sir why
I am taking
x
as extension.
Log in to reply
@A Former Brilliant Member – If you are taking x as extension then why is x ( 0 ) = 2 ? Also, why have you defined spring force as − 1 6 ( x + 1 ) ? Does not make sense.
@A Former Brilliant Member – You need to fix two things:
-
The spring force expression in your equation of motion. This will modify your result slightly.
-
The expression for potential energy.
@Karan Chatrath x = x T o t a l l e n g t h − L 0
Log in to reply
In our discussion, I have assumed that you have complied with the nomenclature that I have used in the problem statement. There x is not an extension but it is a coordinate. You need to explain these things more clearly in your working.
Moreover, if you used x as extension, then x ( 0 ) = 2 is not a correct initial condition. I admire your attempt, but your solution is flawed.
Log in to reply
@Karan Chatrath
no ,sorry.
Consider x as length in 1st page
Consider x as y in second page and
y
=
x
−
L
0
Therefore I am getting correct answer.
@Karan Chatrath
in first page consider
x
as length and in second page consider
x
as extension.
It is a variable.
I don't think it will create any confusion.
I know it is my mistake .
@Karan Chatrath
Sir can we solve integration using Laplace??
Thanks in advance.
Log in to reply
Yes, but it depends on the type of integral
Log in to reply
@Karan Chatrath
The link which you have provided me have that??
That how to solve Integration using Laplace transform??
Log in to reply
@A Former Brilliant Member – Since the Laplace transform is itself an integral, it can u=be used to evaluate integrals which are similar to its form. So yes, the link I shared is useful.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
please I want one example
Integrate this using Laplace
∫
sec
x
+
1
d
x
Thank you very much in Advance.
Please reply.
Log in to reply
@A Former Brilliant Member – I said in my previous comment that integrals of a similar form as the Laplace transform definition can be evaluated using Laplace. Moreover, indefinite integrals cannot be solved using Laplace.
The form which can be evaluated using the Laplace transform is:
I = ∫ 0 ∞ e − s t f ( t ) d t
Using the given data, we get the equations
1 0 j I 1 + 5 j I 2 = 1 0
5 j I 1 + 1 0 j I 2 = 1 0 I 2 ⟹ I 1 = j 2 ( 1 − j ) I 2
Solving we get
I 2 = 4 − 3 j 2 ⟹ E 2 = I 2 R = 4 − 3 j 2 0
⟹ ∣ E 2 ∣ = 4 2 + 3 2 2 0 = 4


@Alak Bhattacharya has already provided a solution to the problem. I am addressing the bonus question.
Say we define a factor f , called the 'dividing factor' which increases from 1 to any large number in small steps and the impedances vary with this factor as such:
Z S = j f 1 0 Z M = j f 5
So this way, the effect of scaling down the impedances can be analysed.
One can see here that as the impedances get scaled-down, the transformer's behaviour converges to that of an ideal step down transformer with the output voltage magnitude tends towards being half of the source voltage magnitude.
I hope my conclusion is correct.