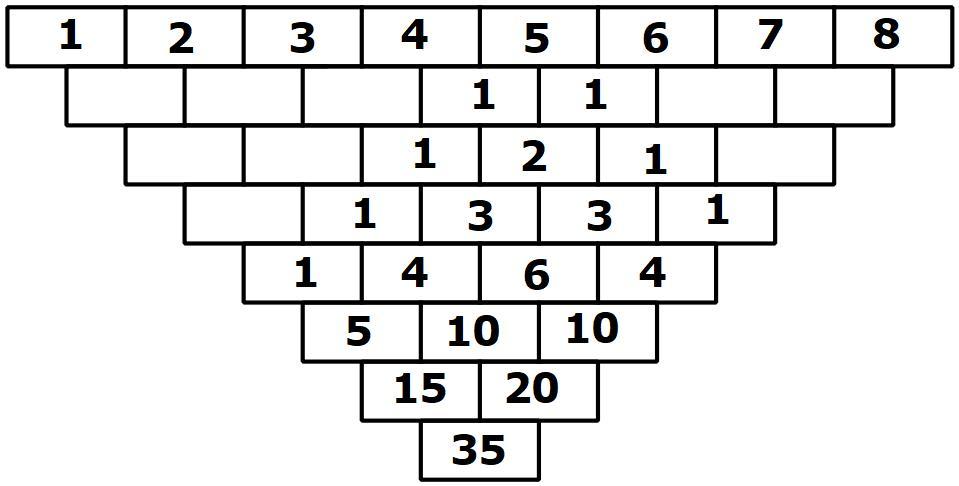
Triangle and numbers

The values in the second row and thereafter denote the number of zeroes present in that number.

The number of trailing zeroes is the number of factors $10 = 2\cdot 5$ present; since there are many more even numbers than factors 5 in the problem, the number of trailing zeroes is equal to the number of factors 5 .

Since each factor 5 must eventually come from the "5" at top, we must consider how many pathways there are from the "5" to the bottom circle .

Each of these pathways consists of 4 steps "southwest" and 3 steps "southeast". Therefore the number of pathways, and thus the number of trailing zeroes, is $\binom 7 3 = \frac{7\cdot 6\cdot 5}{3 \cdot 2 \cdot 1} = 7 \cdot 5 = \boxed{35}.$

The second row will be $(1^12^1, 2^13^1, 3^14^1, 4^15^1, 5^16^1, 6^17^1, 7^18^1)$ , the third row will be $(1^12^23^1, 2^13^24^1, 3^14^25^1, 4^15^26^1, 5^16^27^1, 6^17^28^1)$ , the fourth row will be $(1^12^33^34^1, 2^13^34^35^1, 3^14^35^36^1,4^15^36^37^1, 5^16^37^38^1)$ , and so on. We can observe that the pattern of exponents for each digit follows the numbers of Pascal's Triangle , since the exponents for each digit is the sum of the exponents of the digits in the line before. Therefore, the final number will be $1^12^73^{21}4^{35}5^{35}6^{21}7^78^1$ , and since $5^{35}$ is the greatest factor that is a multiple of $5$ , and $2^{35}$ is also a factor (from $4^{35}$ ), $10^{35}$ is the greatest factor that is a multiple of $10$ , so the final number ends in $\boxed{35}$ zeros.

To find the value of the bottom circle, first, I tried to simplify the problem. With one number, $a$ , the value of the bottom circle $a$ ; With two numbers, $a$ and $b$ , its value is $ab$ ; With three numbers, its value is $a{ b }^{ 2 }c$ ; With four number, $a{ b }^{ 3 }c^{ 3 }d$ ;... We can realize that the power of each number in each pattern, from left to right, corresponds to the numbers in Pascal's triangle. Hence, we can calculate the value of the bottom circle in the picture: it equals to ${ 1 }^{ 1 }\times { 2 }^{ 7 }\times { 3 }^{ 21 }\times { 4 }^{ 35 }\times { 5 }^{ 35 }\times { 6 }^{ 21 }\times { 7 }^{ 7 }\times { 8 }^{ 1 }$ . However, we are only caring​ about the number of trailing zeros, so we can remove the prime factors that are neither 2 nor 5. We get ${ 2 }^{ 101 }\times { 5 }^{ 35 }$ . Since $101>35$ , there are 35 trailing zeros in the number at the bottom.

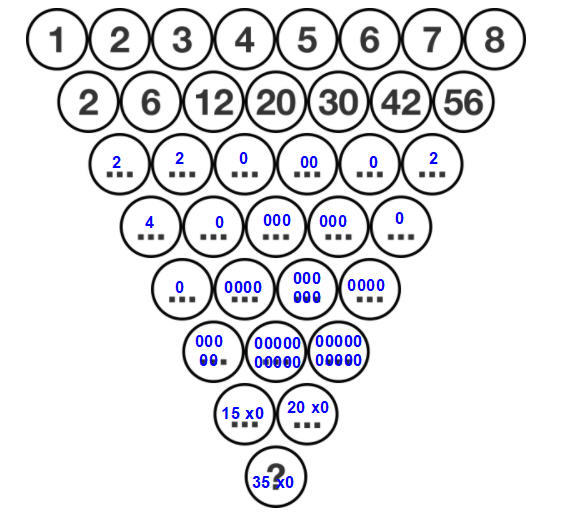
see below for the trailing 0 for each number of each row

Not a solution, but a question...how do we not know whether or not other products, or child products, when multiplied together, will also give a number with a trailing zero? I've looked at the times tables to see that indeed, only numbers which are multiples of 5 or 10 result in numbers with trailing zeroes, but I would deem this a little too naive. Or am I looking at this the wrong way?

The amount of trailing zeroes is equal to the least between the amount of factors of 5 and 2.

there are many more factors of 2 than 5 (4 has two factors of 2 and its placed symmetrically in the triangle compared to 5

Then its only a matter of realising the amount of factors of 5 in each number form a pascal's triangle. Since you multiple two adjacent numbers, you multiply the factors, which means the amount of factors increase additively.

Going doing the triangle shows the final spot coincides with 35, thus that is our answer.

A Python scripting approach:

lines = [[x for x in range(1, 9)]]

while len(lines[-1]) > 1:
    lastline = lines[-1]
    newline = []

    for i in range(len(lastline) - 1):
        newline.append(lastline[i] * lastline[i + 1])

    lines.append(newline)

for line in lines:
    print(line)

lastvalue = str(lines[-1][0])

zeroes = 0

while lastvalue[-1] == '0':
    zeroes += 1
    lastvalue = lastvalue[:-1]

print('Zeroes:', zeroes)

This will output:

[1, 2, 3, 4, 5, 6, 7, 8]
[2, 6, 12, 20, 30, 42, 56]
[12, 72, 240, 600, 1260, 2352]
[864, 17280, 144000, 756000, 2963520]
[14929920, 2488320000, 108864000000, 2240421120000]
[37150418534400000, 270888468480000000000, 243901204807680000000000]
[10063619980174622195712000000000000000, 66070023830779248141926400000000000000000000]
[664903611914043473202543232567979684173499596800000000000000000000000000000000000]
Zeroes: 35

See https://github.com/alcibiade/brilliant/blob/master/2018-02-26/l2-problem3.py

If you multiply them you will get this.... 3,897,583,913,560,042,260,642,265,383,304,444,890,358,227,979,468,800,000,000,000,000,000,000,000,000,000,000,000 i did it on my phone

Mathematica

NestList[(Times@@@Partition[#,{2},1])&,Range@8,7]

gives
{1, 2, 3, 4, 5, 6, 7, 8}, {2, 6, 12, 20, 30, 42, 56}, {12, 72, 240, 600, 1260, 2352}, {864, 17280, 144000, 756000, 2963520}, {14929920, 2488320000, 108864000000, 2240421120000}, {37150418534400000, 270888468480000000000, 243901204807680000000000}, {10063619980174622195712000000000000000, 66070023830779248141926400000000000000000000}, {664903611914043473202543232567979684173499596800000000000000000000000000000000000}