Triangle Area and Slopes

Geometry Level 3

If x x is the length of one side of a triangle with a slope of zero, m 1 m_1 and m 2 m_2 are the slopes of the other two sides, and A A is the area of the triangle, then these four variables are related by the equation x P = Q ⋅ A ( m 1 R − m 2 S ) , x^P = Q \cdot A\big(m_1^R - m_2^S\big), where P P , Q Q , R R , and S S are non-zero integers.

Find ∣ P ∣ + ∣ Q ∣ + ∣ R ∣ + ∣ S ∣ . |P| + |Q| + |R| + |S|.


The answer is 6.

David Vreken by David Vreken , 42, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

David Vreken
May 8, 2018

The area of △ X Y Z \triangle XYZ (with sides x x , y y , and z z , with x along the x-axis and Z Z at the origin) is A = 1 2 x y sin ⁡ Z A = \frac{1}{2}xy \sin Z .

By law of sines, y sin ⁡ Y = x sin ⁡ X \frac{y}{\sin Y} = \frac{x}{\sin X} , so y = x sin ⁡ Y sin ⁡ X y = \frac{x \sin Y}{\sin X} , which means A = x 2 sin ⁡ Y sin ⁡ Z 2 sin ⁡ X A = \frac{x^2 \sin Y \sin Z}{2 \sin X} .

By the angle sum of a triangle, X = 180 ° − ( Y + Z ) X = 180° - (Y + Z) , so sin ⁡ X = sin ⁡ ( 180 ° − ( Y + Z ) ) = sin ⁡ ( Y + Z ) \sin X = \sin (180° - (Y + Z)) = \sin (Y + Z) . Therefore, A = x 2 sin ⁡ Y sin ⁡ Z 2 sin ⁡ ( Y + Z ) A = \frac{x^2 \sin Y \sin Z}{2 \sin (Y + Z)} .

Using the sine addition identity, A = x 2 sin ⁡ Y sin ⁡ Z 2 ( sin ⁡ Y cos ⁡ Z + sin ⁡ Z cos ⁡ Y ) A = \frac{x^2 \sin Y \sin Z}{2 (\sin Y \cos Z + \sin Z \cos Y)} .

Rearranging, x 2 = 2 A ( cos ⁡ Z sin ⁡ Z + cos ⁡ Y sin ⁡ Y ) x^2 = 2A(\frac{\cos Z}{\sin Z} + \frac{\cos Y}{\sin Y}) or x 2 = 2 A ( 1 tan ⁡ Z + 1 tan ⁡ Y ) x^2 = 2A(\frac{1}{\tan Z} + \frac{1}{\tan Y}) .

Since m 1 = tan ⁡ Z m_1 = \tan Z and m 2 = tan ⁡ ( 180 ° − Y ) = − tan ⁡ Y m_2 = \tan (180° - Y) = -\tan Y , x 2 = 2 A ( 1 m 1 − 1 m 2 ) x^2 = 2A(\frac{1}{m_1} - \frac{1}{m_2}) or x 2 = 2 A ( m 1 − 1 − m 2 − 1 ) x^2 = 2A(m_1^{-1} - m_2^{-1}) .

This means P = 2 P = 2 , Q = 2 Q = 2 , R = − 1 R = -1 , and S = − 1 S = -1 , and ∣ P ∣ + ∣ Q ∣ + ∣ R ∣ + ∣ S ∣ = ∣ 2 ∣ + ∣ 2 ∣ + ∣ − 1 ∣ + ∣ − 1 ∣ = 6 |P| + |Q| + |R| + |S| = |2| + |2| + |-1| + |-1| = \boxed{6} .

2 Helpful 0 Interesting 0 Brilliant 0 Confused

The tricky step was finally realizing that

m 1 + m 2 m 1 m 2 = m 1 − 1 + m 2 − 1 \dfrac{m_1 +m_2}{m_1 m_2} = m_1^{-1}+ m_2^{-1}

when once the area has been worked out first in this way

A = m 1 m 2 x 2 2 ( m 1 + m 2 ) A=\dfrac{m_1 m_2 x^2}{2(m_1 + m_2)}

Michael Mendrin - 3 years, 1 month ago

In general, it is not true that m 1 = tan ⁡ Z m_1 = \tan Z and m 2 = tan ⁡ Y m_2 = \tan Y .

Jon Haussmann - 3 years ago

Log in to reply

"Through trigonometry, the slope m m of a line is related to its angle of incline θ \theta by the tangent function m = tan ⁡ ( θ ) m= \tan(\theta) ." (See here .)

David Vreken - 3 years ago

Log in to reply

The problem is, in your solution, Y Y and Z Z are angles of the triangle (shown in red below).

The formula m = tan ⁡ θ m = \tan \theta only works when θ \theta is the angle the line makes with a horizontal line (shown in blue below). These are different angles.

Jon Haussmann - 3 years ago

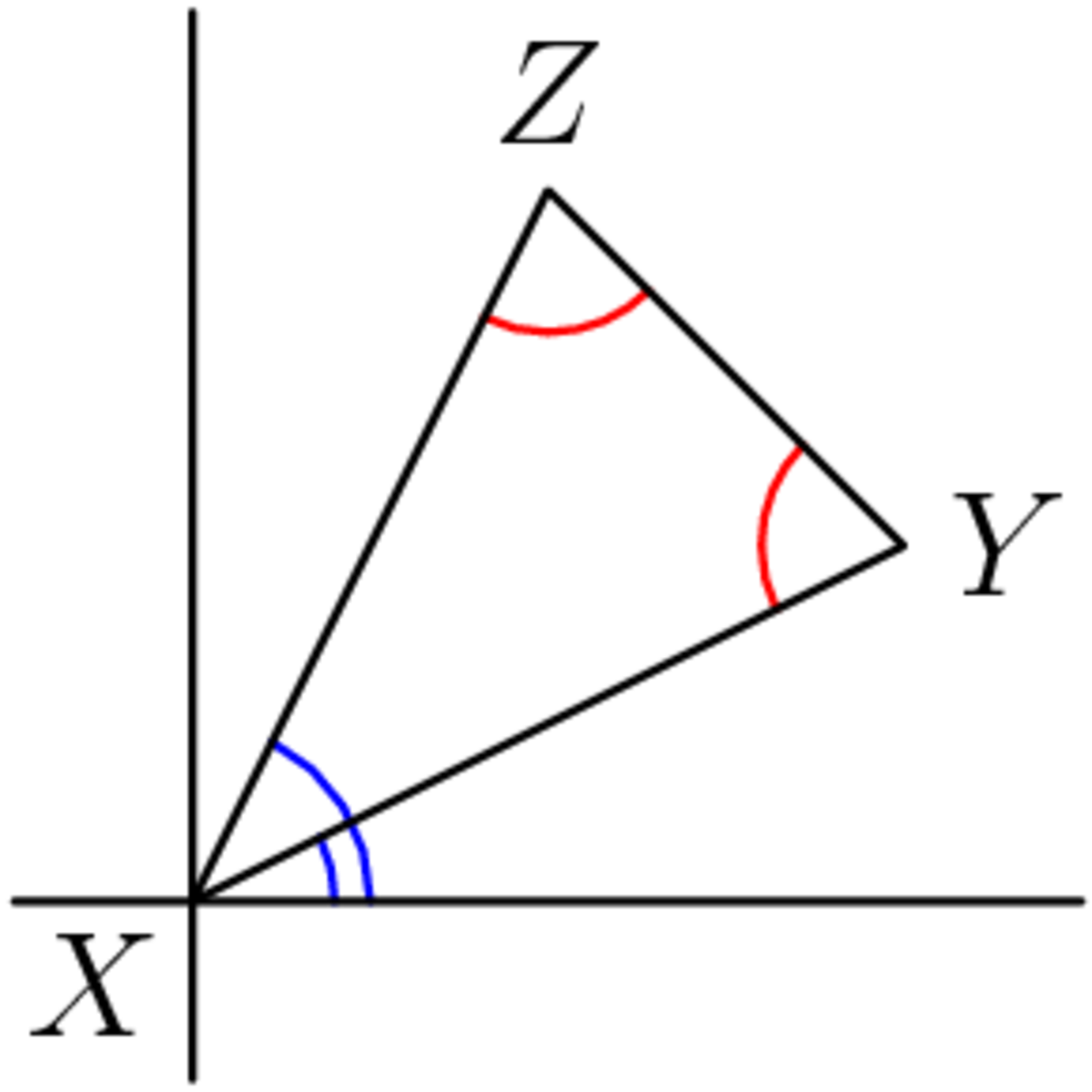
Log in to reply

@Jon Haussmann – You are right! I edited my problem to restrict side x to have a horizontal slope.

David Vreken - 3 years ago

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...