Triangle-Ception III
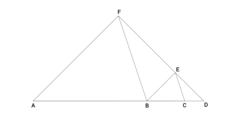 In the figure above,
△
A
B
F
∼
△
B
C
E
, with
∠
F
A
B
=
∠
E
B
C
and
∠
A
F
B
=
∠
B
E
C
=
1
0
9
∘
.
In the figure above,
△
A
B
F
∼
△
B
C
E
, with
∠
F
A
B
=
∠
E
B
C
and
∠
A
F
B
=
∠
B
E
C
=
1
0
9
∘
.
Additionally, points A , B , C , D are collinear and points D , E , F are collinear.
Given that A C = 8 and B D = 6 , the length of A D can be expressed in the form m + n p where m , n , p are positive integers, and p is not divisible by the square of any prime.
Find m + n + p .
The answer is 19.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Nice method. Can you please explain how you got B D A D = B C A B ?
Log in to reply
two similar triangles have their corresponding sides in the same ratio!!
Log in to reply
Yes but how do you say they are similar? I think that has to be prove!! Please correct me if I am wrong.
Log in to reply
@Niranjan Khanderia – consider two equilateral triangles. One with side 3units another with 5units. Have a look at the ratio of their corresponding sides...!!
And also, two triangles are similar only if all the corresponding angles are equal!!
First, let's continue the pattern of similar triangles from C towards point D . These similar triangles cannot ever reach exactly point D due to the construction of the diagram, but they will get closer and closer.
Due to the similarity of these infinitely many triangles, we have an infinite geometric progression of bases, whose sum is equal to A D . Let's call the first base A B . Let A B = a , and A D = x . We know the value of our infinite geometric series:
x = 1 − r a
We also know that x = a + 6 due to given information, so we have
a + 6 = 1 − r a
We also can tell that the base of the second similar triangle in our progression is a r , so we know from the given information that:
a + a r = 8
Now we have a system of two equations and two variables. Solving for a gives:
0 = a 2 + 4 a − 4 8
Quadratic formula gives:
a = 2 − 4 ± 4 1 3
We can ignore the minus solution, since a > 0 due to it being a side length. We are left with:
a = 2 1 3 − 2 .
A D = x = a + 6 = 4 + 2 1 3 .
4 , 2 , 1 3 are all positive integers and 1 3 is not divisible by the square of any prime, so our answer is:
2 + 4 + 1 3 = 1 9
Also, the angle I gave you was just a red herring. It doesn't matter what the angles are in the similar triangles. For a visual proof, check out this desmos graph I made Adjust the values of slider B and C . The angles change, but the intersection with the x axis does not.
I think you did it using similarity?, You gave a nice solution for it but I used only the use of parallel lines are Thales Theorem. Upvoted:-)
Though not so simple, it is an intelligent out of box approach. Congratulations. I did not up vote the method only because there was a simple method. But greatly appreciate your method.
This is only to give a different approach. Lu Chee Ket's is a beautiful method. L e t B C = x , a n d C D = y , B C A B = k ∴ x = k + 1 8 , x + y = 6 . ∠ F A B = ∠ E B C ∴ F A ∣ ∣ E B . ∴ k = E B F A = B D A D = 6 8 + y ⟹ y = 6 k − 8 . 6 = x + y = k + 1 8 + 6 k − 8 . ⟹ 3 k 2 − 4 k − 3 = 0 . S o l v i n g f o r p o s i t i v e k , k = 2 ∗ 3 4 + 1 6 + 3 6 = 3 2 + 1 3 . A D = 1 4 − x = 1 4 − k + 1 8 = 1 4 − 3 2 + 1 3 + 1 8 R a t i o n a l i s i n g A D = 1 4 − 2 5 − 1 3 2 4 ∗ ( 5 − 1 3 ) = 1 4 − 1 0 + 2 ∗ 1 3 = m + n ∗ p m + n + p = 1 9
If we let x = B C , then we have that
B D A D = 6 1 4 − x = B C A B = x 8 − x
1 4 x − x 2 = 4 8 − 6 x
x 2 − 2 0 x + 4 8 = 0
( x − 1 0 ) 2 = 1 0 0 − 4 8 = 5 2
x = 10 - 2 1 3 = 2.7889 (Where 6 - x > 0)
AD = 14 - x = 14 - (10 - 2 1 3 ) = 4 + 2 1 3
Therefore, m + n + p = 4 + 2 + 1 3 = 1 9
Note that the triangle is not fixed as E and F are uncertain. Only the dimensions on the base line are fixed. Despite this, the proportion of ratios can be applied.