This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Moderator note:
How would you generalize this to a triangle of side length n?
Can it be generalised for eq. triangle with side "n"?
Log in to reply
There is an actual formula for this, namely ⌊ 8 n ( n + 2 ) ( 2 n + 1 ) ⌋ , as found here .
A discussion on this problem, with a variety of approaches, can be found here .
Log in to reply
Yes, this seems to work. I was trying n^2+((n-1)^2-(n-2))+((n-2)^2-(n-3))....+(1^2-0). This fitted everything till n=4, but for n=5, the answer should be 48 while my formula gives 49.
i agree.. n=4
what is n actually???
I missed the big inverted one. Rushing the answer, I forgot about Morley triangles. It is the same configuration of three sets of four parallel lines forming 27 triangles.
Illuminati confirmed! Calvin Lin!
I almost missed the length 2 inverted triangle. To my eye having the triangles colored made this triangle less discernible when compared to a more 'standard' uncolored line drawing.
There are 1 + 3 + ... + (2n-1) = n^2 equilateral triangles of unit length of each side. (in the spec. case shown, n=4 but this formula holds in general.)
In the special case n=4: - there are 7 triangles with each side of length 2; - there are 3 triangles with each side of length 3; - and of course, 1 triangle w/ sides of length 4.
It would be nice to derive a general formula for the side lengths of 2, ..., up to n (where obviously there's exactly one triangle with each side of length n).
One big inverted.
the big inverted one...
The inverted one
I missed the one inverted big triangle made up of 4 smaller ones -_-
big inverted
but i found 31 triangles in that triangle
Log in to reply
maybe you counted some triangles twice!
Can you explain how you counted 31 triangles?
Log in to reply
I dont know how i can explain it to you. we can find may triangular disigns in it.
Log in to reply
@Milan Varghese – Can you add a diagram? Which triangle of yours am I not counting?
Log in to reply
@Calvin Lin – how can i do that? sorry for the late replay. i don't visit the site very frequesntly
Nice picture. Thanks for including it!
Log in to reply
Since you're from the staff, I thought it would be a good idea to tell you this, even if the problem is bit old. I did choose option 27, and yet it shows that the correct answer is 30.
Count all individual triangles for a total of 16. Now group 4 triangles together to make one larger triangle. Count them up and you get 6 that are right side up and one in the center which is inverted, leading to a total of 7. 16+7 is 23. Now group 9 triangles together and count those triangles. You get 3, so now you're up to 26. Count the whole triangle as one more and you get 27
I just counted them... is that not right or do I have to do all this crazy equation stuff? :/
I somehow multiplied them together in my head.... I have no idea how I do the math haha. Must have been luck.
Simply counting is great!
1+3+5+7 = 16 single triangles 1+2+4 = 7 triangles from 4 single triangles 1+2 = 3 triangles from 10 single triangles And the big triangle as a whole
Therefore, 16+7+3+1 = 27 triangles.
16 small triangles blue and red ones. 7 medium triangles(each one with4 small triangles). 3 big triangles(each one with 9 small ttriangles). 1 huge one (with all the small triangles). 16+7+3+1=27
Illuminati confirmed! Epic maymays!
There are basically 27 triangles. Make bigger triangles from smaller triangles. Even the triangle that holds all the triangles. And look for some very cheeky triangles that are hiding. That's basically the answer. No Algebra Stuff and things. Just believe in your 2-D Shapes.
I just kinda counted them and squinted my eyes so i could see past the repetitions that confuse me regularly.
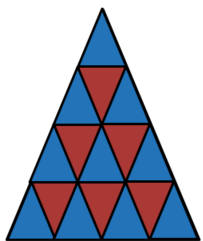

There are 10 length 1 upright equilateral triangles (the blue ones),
6 length 2 upright equilateral triangles,
3 length 3 upright equilateral triangles,
1 length 4 upright equilateral triangle.
There are 6 length 1 inverted equilateral triangles (the red ones),
1 length 2 inverted equilateral triangle (green below).
Hence, there are at total of 1 0 + 6 + 3 + 1 + 6 + 1 = 2 7 triangles in the image.
Did you miss the 7 inverted triangles, or the 1 big inverted triangle?