Triangle of Medians
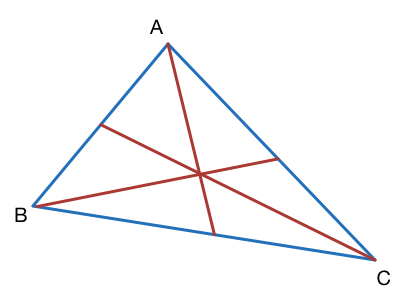 Triangle
A
B
C
has sides of length 24, 35, and 53.
Triangle
A
B
C
has sides of length 24, 35, and 53.
Triangle D E F has side lengths equal to the lengths of the three medians of triangle A B C .
Find the area of triangle D E F .
The answer is 252.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
By the way, I did not understand this proof. Can you explain me how do you get these numbers 6 1 and 4 1 ? I calculated median lengths and then found the area. Thanks
Log in to reply
For the 6 1 , the three segments drawn are the medians of the triangle, meeting at the centroid. The centroid divides each median into a 2:1 ratio. This, plus the fact that triangles with equal bases and equal heights have equal areas, leads you to the conclusion (details left to the reader) that the six small triangles have the same area, so each of them is 6 1 the area of the whole triangle.
In the second diagram, when you join the midpoints of the sides of any triangle, you create four smaller triangles all congruent to each other (because they all are made of the same three sides). So each one is 4 1 the area of the whole triangle.
The four shaded triangles can be assembled into a second triangle, where each side is the length of one of the medians of the original triangle (see top-left diagram). And its area is 4 1 + 3 ⋅ 6 1 = 4 3 that of the original triangle.
Log in to reply
Woww.. Thanks Sir!
In the third diagram I don't see how you know the small triangle in the midle is 4 1
Log in to reply
@Francisco Rodríguez – It is the same gray triangle from the second diagram.
Fantastic!! I so love such geometric solutions..
First, hats off to Matt!! Here is a vector solution -
 Imgur
Imgur
Let the triangle be formed by three vectors a , b , c such that a + b + c = 0
Its area will be half the cross product of any two vectors like 2 a × b
Denoting median on vector c = C = 2 a − b
By symmetry, A + B + C = 0 . Thus medians must form a closed polygon (triangle) when placed cyclically!
Area of such a triangle = 2 A × B = 4 1 ( b − c ) × ( c − a ) = 4 1 ( b × c − c × c − b × a + c × a )
Expanding and plugging c × c = 0 and b × c = c × a = a × b = − b × a
Thus the area of median triangle is 3/4 area of origina, which is 336 using Heron's formulal
Thus the answer is 2 5 2
That too would involve a lot of calculations.Won't it?
m a 2 = 2 1 ∗ ( b 2 + c 2 ) − 4 1 a 2 = 2 1 ∗ ( a 2 + b 2 + c 2 ) − 4 3 a 2 = 1 8 7 3 . m b 2 = 2 1 ∗ ( a 2 + b 2 + c 2 ) − 4 3 b 2 = 1 3 8 6 . 2 5 . m c 2 = 2 1 ∗ ( a 2 + b 2 + c 2 ) − 4 3 c 2 = 1 9 8 . 2 5 . 2 s = m a + m b + m c = 9 4 . 5 9 0 6 , A r e a 2 = s ( s − m a ) ( s − m b ) ( s − m c ) = 6 3 5 0 4 . A r e a = 2 5 2
I used Apollonius Theorem on the three sides and calculated the the three sides and then by appyling heron's theorem I calculated the answer. It came nearly about 252.02
It’s kind tricky, here’s how I understand it, The sides of ∆DEF r d red lines (medians) in ∆ABC,
To find the medians: Assume: AB = 24, AC = 35, BC = 53 Median1: 4m^2 = [2x(35)^2] + [2x(53)^2] – 24^2 m = 43.278 Median2: 4m^2 = [2x(24)^2] + [2x(35)^2] – 53^2 m = 14.0801 Median3: 4m^2 = [2x(24)^2] + [2x(53)^2] – 35^2 m = 37.2324
area (∆DEF) = square-root of[s(s-a)(s-b)(s-c)] --->(I think d s d hero’s formula, search it) (s = (a+b+c)/2)
>AREA = 252.00
…hope I calc. it correctly (◠‿ ◠)
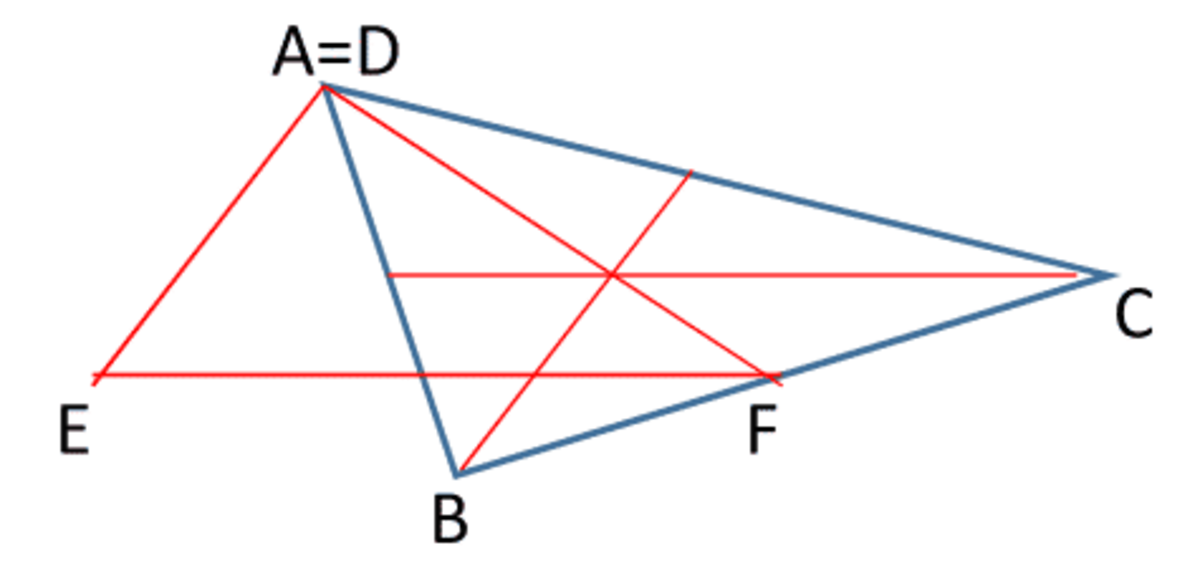
In an equilateral triangle side 1, all medians are 2 3 long. Triangle made of medians in place of the 1's has therefore area 3/4 that of the area of the original triangle. Triangle ABC in the problem can be obtained from a unit equilateral triangle by a linear transformation. Applying this transformation to the entire plane containing both triangles will change the areas of △ A B C and △ D E F , but it will not change the ratio of these areas. Therefore area of △ D E F will still be 3/4 of the area of △ A B C , and 3/4 of 336 is 252.
Mr Enlow's demonstration is, of course, very nice. For those of us who don't mind horrific series of calculations there's Appolonius' theorem, mentioned in https://en.wikipedia.org/wiki/Median_(geometry).
Which makes me wonder if I should have simply given the area of Δ A B C as being 336, and not given any side lengths...
Log in to reply
That would be a bad idea, because then people would know that the area is independent to the side lengths. Given this assumption, they can just look at, for example, an equilateral triangle and find that the area is 4 3 of the area of the original triangle.
With the side lengths, people are at least able to bash it out, with only a few clever people clever enough to realize the relations between the area.
Log in to reply
But in the end they all get the same answer. In general, I like to thwart and/or frustrate the bashers, and reward the more elegant/simple approaches. :-)
Log in to reply
@Matt Enlow – I feel, specifying the sides still has its value. Since one needs to calculate the area of the original triangle even after showing the general 3:4 ratio relationship. Enjoyed that proof! Always love them when they stand by themselves saying nothing!
Log in to reply
@Ujjwal Rane – In response Matt Enlow i am novice learner. could you carry me through in detail explanation ? thanks in advance
Log in to reply
@Emon Khan – See my Jan 14 reply to Snehal Shekatkar above.
The image below is a "proof without words" that a triangle formed by the medians of another triangle has an area that is 4 3 that of the other triangle.
Heron's formula gives the area of Δ A B C as 336, so the area of Δ D E F would be 4 3 ⋅ 3 3 6 = 2 5 2 .