Triangle Properties #1
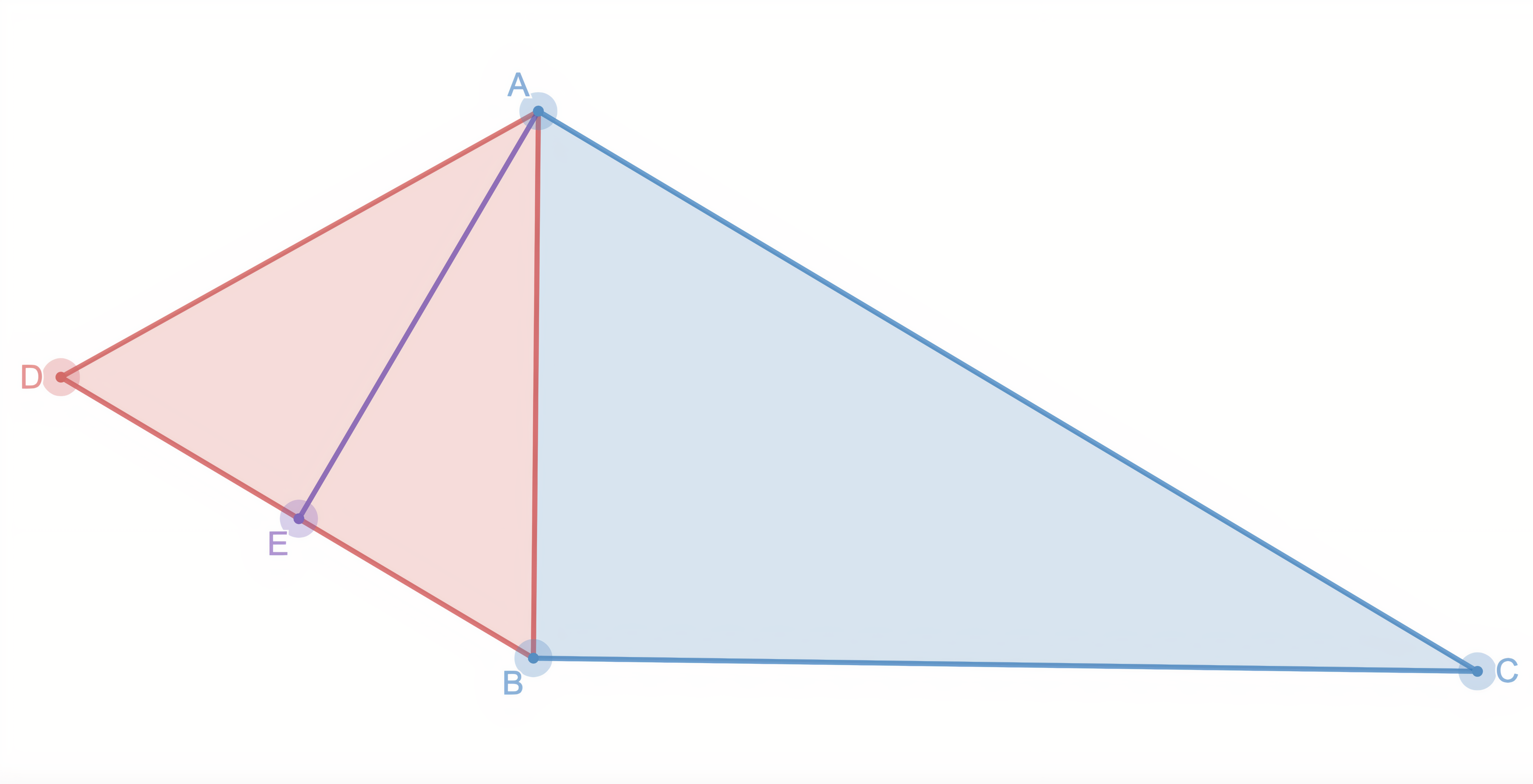
Given that:
-
△ A B C is a right triangle
-
A E is drawn such that A E ⊥ B D and D E = B E .
-
A E = 6 , B D = 7 , ∠ A C B = 3 0 ∘
Find the area of △ A B C to the nearest whole number.
The answer is 42.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Log in to reply
Log in to reply
Sorry I misread the question
@Just C
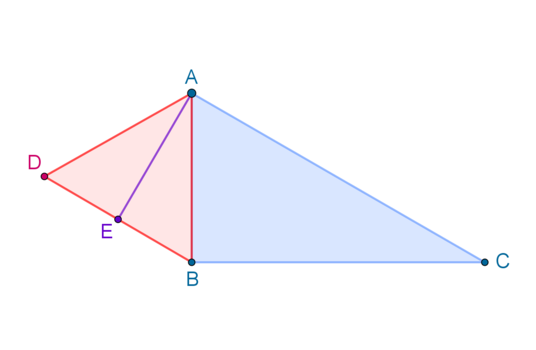
- Perhaps you should mention in your text that the figure is not drawn to scale, otherwise it would look like this:
Log in to reply
@Thanos Petropoulos – That’s true, angle ADE is roughly 60 degrees which is a lot different from 45 (which is what I used in the image). I’ve edited it to show that, might decide to make a more accurate graph later. Thanks for the note! :)
That's given in the problem statement.
ABC triangle area is the half of an equilateral triangle area that is 2 3 ⋅ A B 2 = 2 3 ⋅ ( A E 2 + ( 2 B D ) 2 ) = 2 3 ⋅ ( 6 2 + ( 2 7 ) 2 ) ≃ 4 1 , 8 .
The nearest whole number is 4 2 .
Since △ A B C is a right triangle and ∠ A C B = 3 0 ∘ , we know that A B : A C = 1 : 2 (because sin ( 3 0 ∘ ) = A C A B = 0 . 5 ).
Since A E is drawn such that A E ⊥ B D and D E = B E , we can conclude that △ A B D is isosceles ( S A S postulate of similarity: D E = B E , A E = A E , ∠ A E D = ∠ A E B = 9 0 ∘ , △ A E D is △ A E B scaled by a factor of 1 , and therefore is congruent to △ A E B , then A B = A D ).
Following, we can split B D in half (3.5), and use Pythagoras’ Theorem to obtain A D (and A B ).
A B = A D = A E 2 + D E 2 = 6 2 + 3 . 5 2 .
Since A B : A C = 1 : 2 , A C = 2 6 2 + 3 . 5 2 .
Now, we need to find B C .
B C = ( 2 6 2 + 3 . 5 2 ) 2 − ( 6 2 + 3 . 5 2 ) 2 = 4 ( 6 2 + 3 . 5 2 ) − ( 6 2 + 3 . 5 2 ) = 3 ( 6 2 + 3 . 5 2 ) = 1 4 4 . 7 5
The area of △ A B C is: 2 A B × B C = 2 1 4 4 . 7 5 × 6 2 + 3 . 5 2 ≈ 4 2