Triangle to a hexagon
Construct a square on each side of a triangle with side lengths 3, 4, and 5. Then, construct a hexagon by joining the vertices of the squares which are not vertices of the 3-4-5 triangle.
Find the area of this hexagon.
The answer is 74.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
7 solutions
It is rather surprising to notice that all the triangles have the same area. That simplifies our job to calculating just the nice triangle in the bottom left.
Log in to reply
I was quite surprised too! This means that if we were to join all three triangles together to form a larger triangle, the vertex at which they all join would be the centroid.
Really interesting observation!
yeah I agree, that is where the beauty of the problem lies and also this fact (the 3 triangles have same area) is true for any triangle(need not be right-angled triangle). You can check Ahmad sir's 2nd solution(its in the comments section of his original solution) for a proof. Its through the same way(of this solution). Try it
Log in to reply
I was wondering if that was the case! Just read the solution... it seems obvious now. The outer triangles have two lengths the same as the inner, and the sin of the angle is the same, since one angle is 180 minus the other.
Log in to reply
@Sathvik Acharya how did you draw the figure in the problem?
Log in to reply
@Andrea Virgillito – Not sure what @Sathvik Acharya used, but Figma is also good to use:)
I suspected that the triangles had the same area, but was not certain. Is there a way to show why the 3 triangles are the same area without using trigonometry (for those of us who forgot it over a decade ago)?
Log in to reply
Hmmm imagine if I were to rotate the central triangle 90 degrees anti-clockwise about angle B. Then the height of the upper left triangle would be b . I could do the same for the one on the right. All triangles have height and base of a and b in some order... (PS I've forgotten most of the trig stuff I did last week don't worry)
you can see Ahmad sir's solution (its in the comments section of his original solution) where he explains it with a diagram and the proof is without words though its a bit hard to see this proof and involves some constructions. So maybe trig is the best option.
See my solution below. No trigonometry at all. @Steve Powersuit
Dan Ley how did you draw the figure above?
Log in to reply
I took a screenshot of the figure from the question, and added labels in Adobe Fireworks CS4:)
On your diagram, how do you know those highlighted angles (namely, A and 108-A, or B and 180-B) are supplementary?
Log in to reply
Good question, I guess I kind of left that one to the reader. Angles around a point add up to 360 degrees. There are two 90 degree angles from the squares, therefore the remaining two angles add up to 180 (are supplementary).
Why wouldn't Heron's formula be used here? I used Heron's formula to calculate the two other triangle areas and I got 80 as the answer total.
Log in to reply
How did you calculate the length of the third side of the triangle?
Draw another rectangle R that inscribes the hexagon and whose sides are parallel to the initial triangle catheti. This rectangle is ( 4 + 3 + 4 ) × ( 3 + 4 + 3 ) with an area of 1 1 0 .
The area between R and the hexagon consists of 4 triangles. We calculate the areas.
- The top-left triangle is 2 6 × 4 = 1 2 ,
- the top-right triangle is 2 4 × 3 = 6 ,
- the bottom-left triangle is 2 3 × 4 = 6
- and the bottom-right triangle is 2 8 × 3 = 1 2 .
Finally, subtracting triangles areas from R , the area of the hexagon is 1 1 0 − 1 2 − 6 − 6 − 1 2 = 7 4 .
That's an interesting observation! I've added an image to help others visualize your description.
Can you explain why the rectangle has the side lengths that you mentioned? It's not immediately obvious how to account for the left over region.
Adding to Joan's work, the reason she's able to assume all that is because of how the angles relate to each other, subtracting from 90* and 180*, etc. I could elaborate in more detail later, but doing so now from my phone requires more effort than I'm willing to impart.
Log in to reply
Adding 3x4 triangles to the exterior of the 5×5 square generates a 7x7 square which gives the dimensions of R.
Solving the puzzle turned out to be far easier than finding how to insert a drawing here. ;) Too bad, it's pretty. So I'll just have to describe it: If I add a triangle on top of the 3-square with width 3 and height 4, then connect its top vertex with the uppermost corner of the 5-square, I have two identical triangles, forming a parallelogram. The red diagonal connecting the 3-square to the 5-square bisects this parallelogram. Therefore the orange-shaded triangle has an area of 3X4/2. The same is true for the orange shaded triangles outside the other squares. So we have four triangles of area 3X4/2, +9=16+25.
Log in to reply
When submitting a solution, there is a formatting toolbar at the top. If you click on the picture icon (3rd from the left), you can select a file to upload.

We use markdown notation to display images, which allows you to display them in comments even though there is no formatting toolbar. The notation has the form

. For example, to get the above image, I typed in the code:

yes I think this is the easiest solution. sir and I think with your method we can even prove that AREA of ABC=S1=S2=S3 and for this to happen ABC need not be right-triangle, thus leading to the generalization of the problem.
Log in to reply
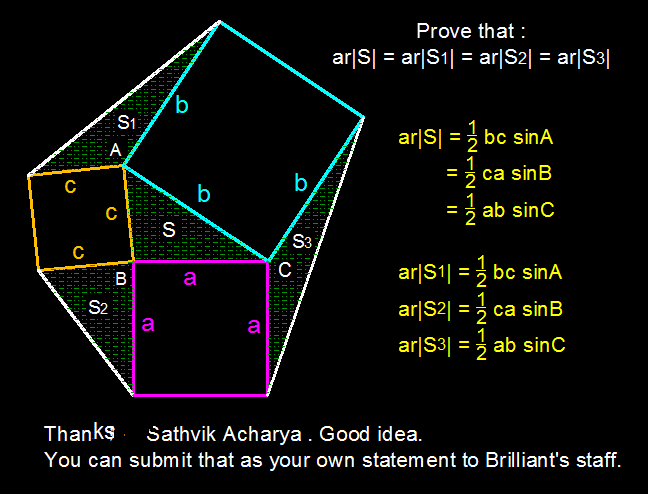
Log in to reply
Right, the key is that S = S 1 = S 2 = S 3 .
yes that's correct so we know a nice fact now. I am just wondering can we solve the same problem without trigonometry, though this is an obvious approach
Log in to reply
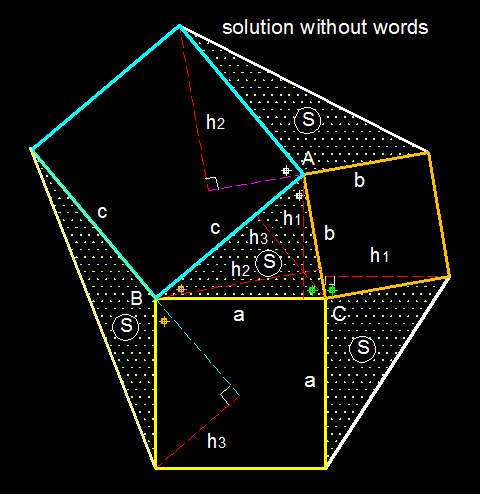
Log in to reply
Ah! Among all the solutions here, this is my favorite. Thanks for sharing! Indeed, we don't need to use any words at all!
sir what are you using for your geometric figures? can I know the website or software that you are using please as it seems pretty good
Log in to reply
That's AutoCad software . You can get it free on the World Wide Web. Go to Google.com. Enter the word : AutoCad software.
AutoCAD is used across a wide range of industries, by architects, project managers, engineers, graphic designers, and many other professionals.
thank you sir. sure I can learn more with this software.
What is the rule that says 1/2 * side * side * sin(theta) = the area of a triangle?
Log in to reply
Well, it is just the fact that 2 1 × b × h = Δ . s i d e × sin θ gives you the perpendicular distance to the other side.
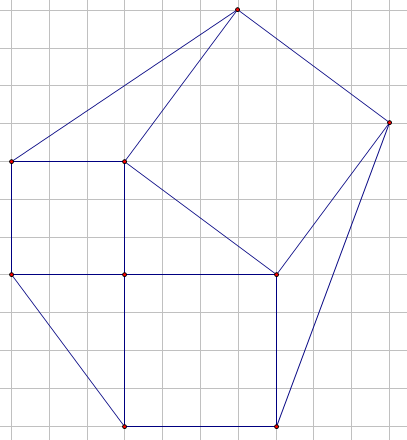 After finding the area of the rectangle surrounding the hexagon (11x10=110)
Take away the 4 triangles in the corners (12,12,6,6)
110-12-12-6-6=74
After finding the area of the rectangle surrounding the hexagon (11x10=110)
Take away the 4 triangles in the corners (12,12,6,6)
110-12-12-6-6=74
It is possible to do this without any trigonometry.
We will solve for the general case, i.e. a triangle with side lengths
a
,
b
,
c
.
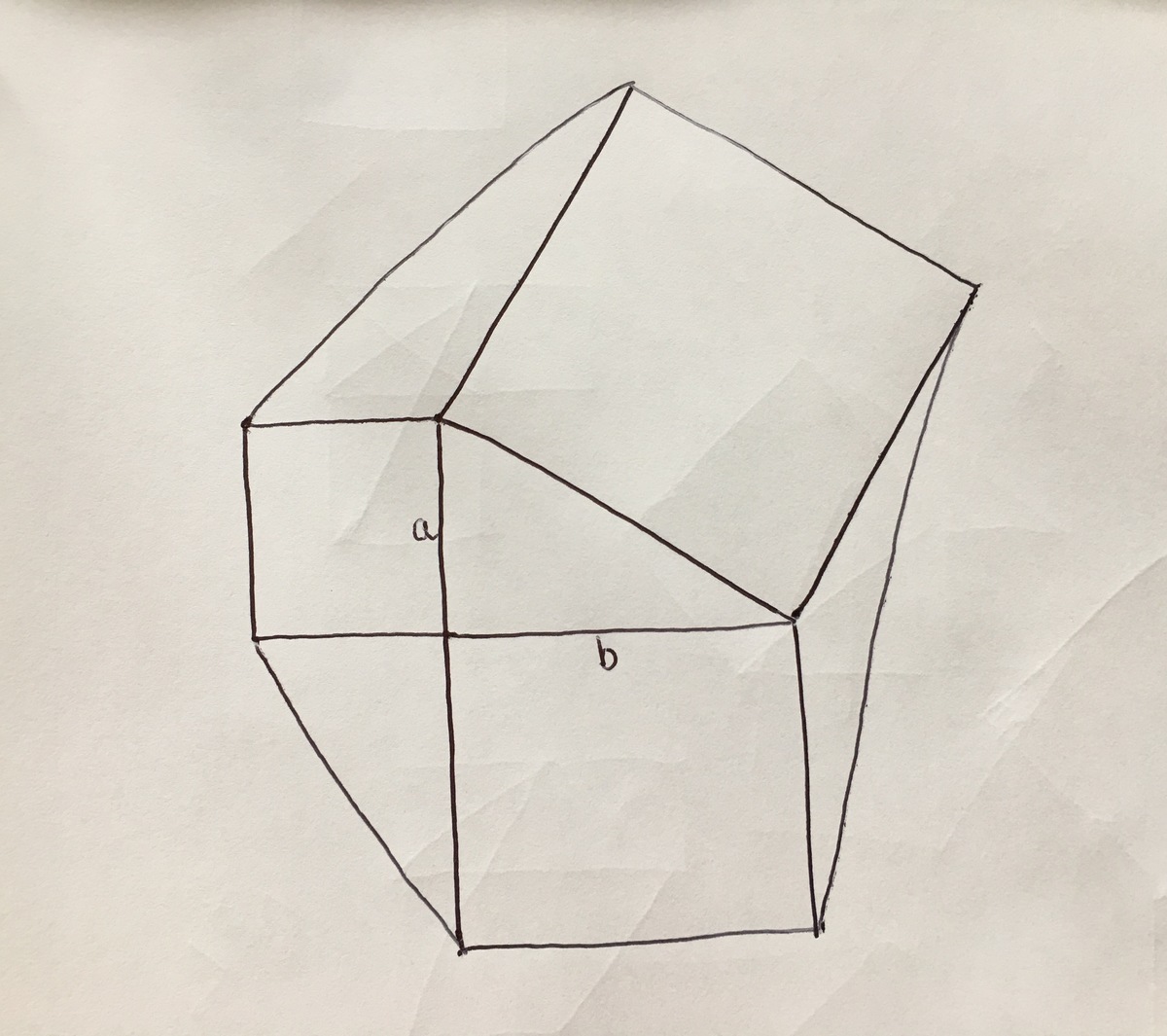 We will continue the side length of the largest square down through the smallest square (the
a
×
a
one), like so:
We will continue the side length of the largest square down through the smallest square (the
a
×
a
one), like so:
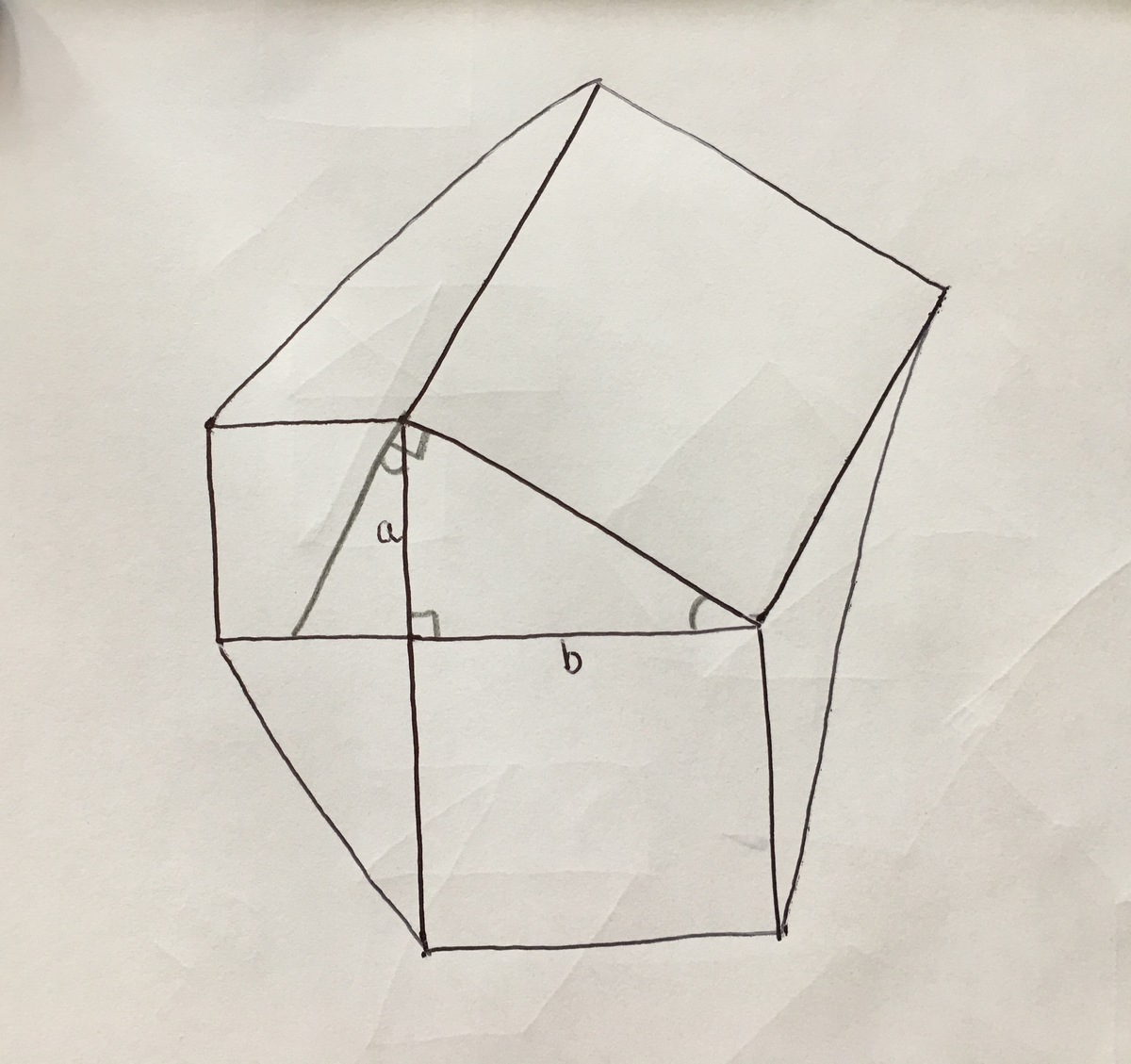 The same thing can be done on the other side, through the
b
×
b
square.
The same thing can be done on the other side, through the
b
×
b
square.
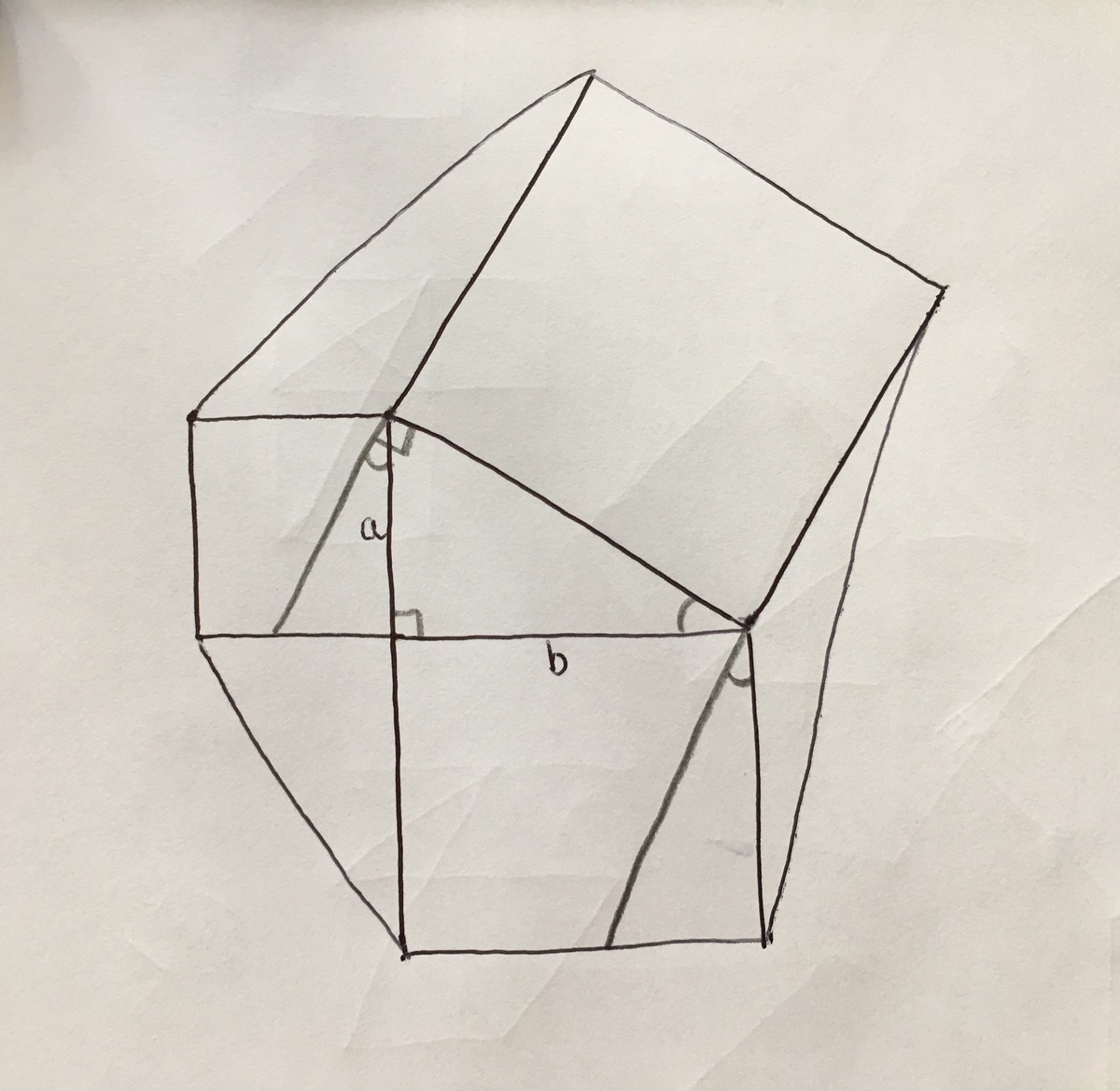 We can now add a perpendicular to that line from the corner of the
a
×
a
square. This creates two congruent triangles (one side and two angles are equal).
We can now add a perpendicular to that line from the corner of the
a
×
a
square. This creates two congruent triangles (one side and two angles are equal).
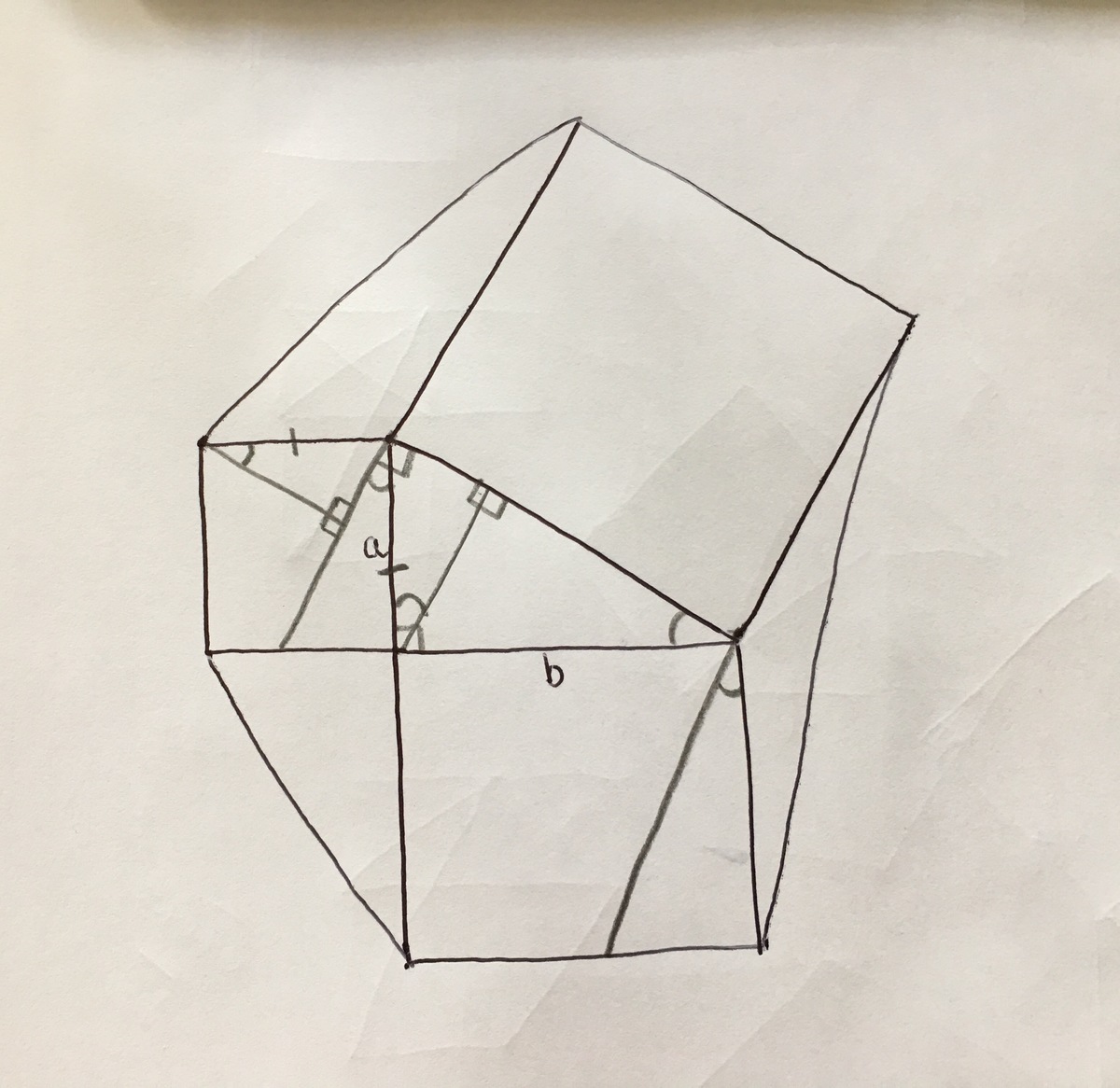 Likewise, through the
b
×
b
square. The pairs of congruent triangles are shaded.
Likewise, through the
b
×
b
square. The pairs of congruent triangles are shaded.
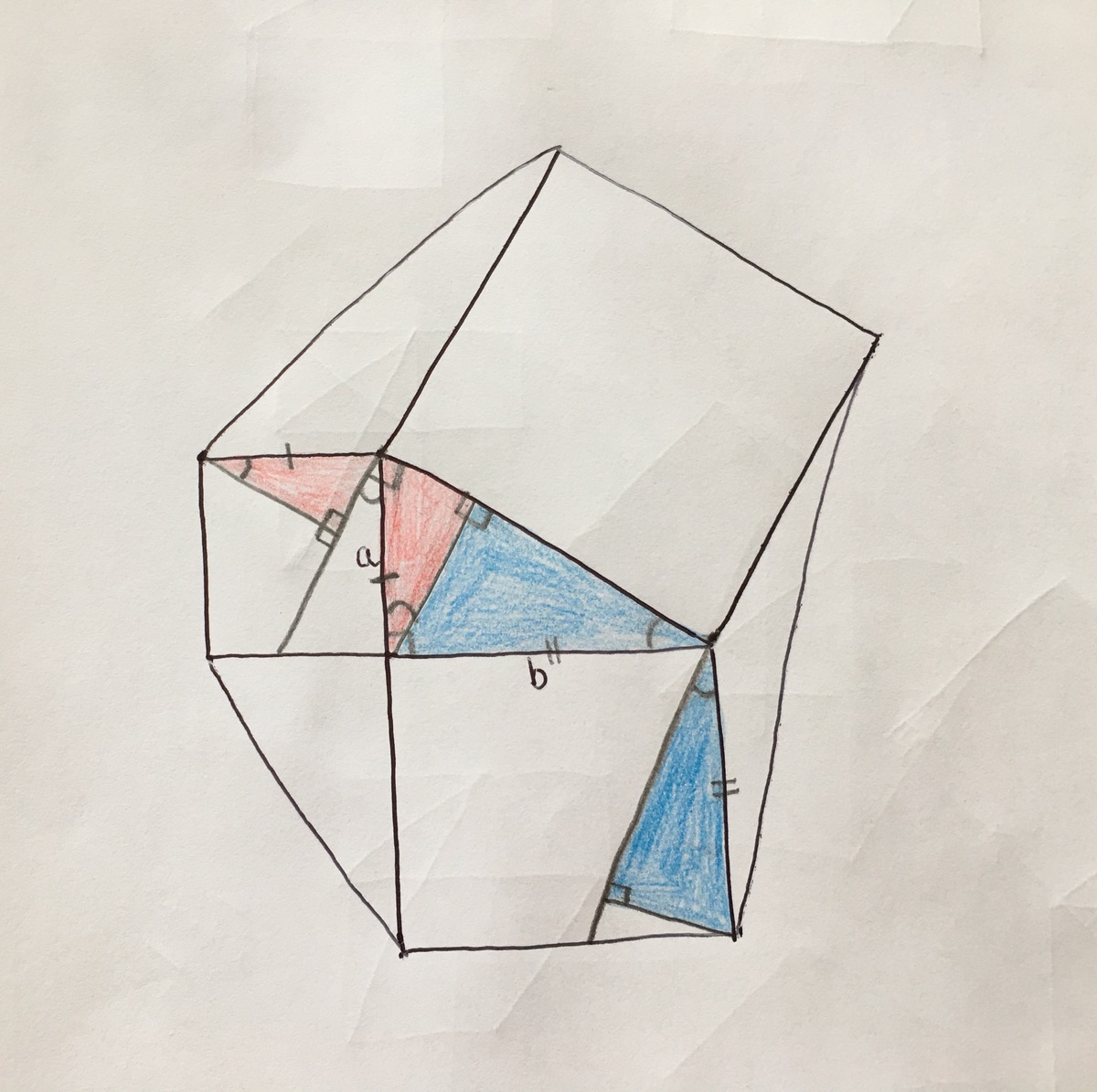 Since the two triangles in each pair are congruent, and two triangles from different pairs share a height (the two in the original
a
,
b
,
c
triangle), all the heights must be equal. The two unshaded triangles have a common base (it is the side length of the largest square). And because they both have the same base and the same height, their areas must be equal!
Since the two triangles in each pair are congruent, and two triangles from different pairs share a height (the two in the original
a
,
b
,
c
triangle), all the heights must be equal. The two unshaded triangles have a common base (it is the side length of the largest square). And because they both have the same base and the same height, their areas must be equal!
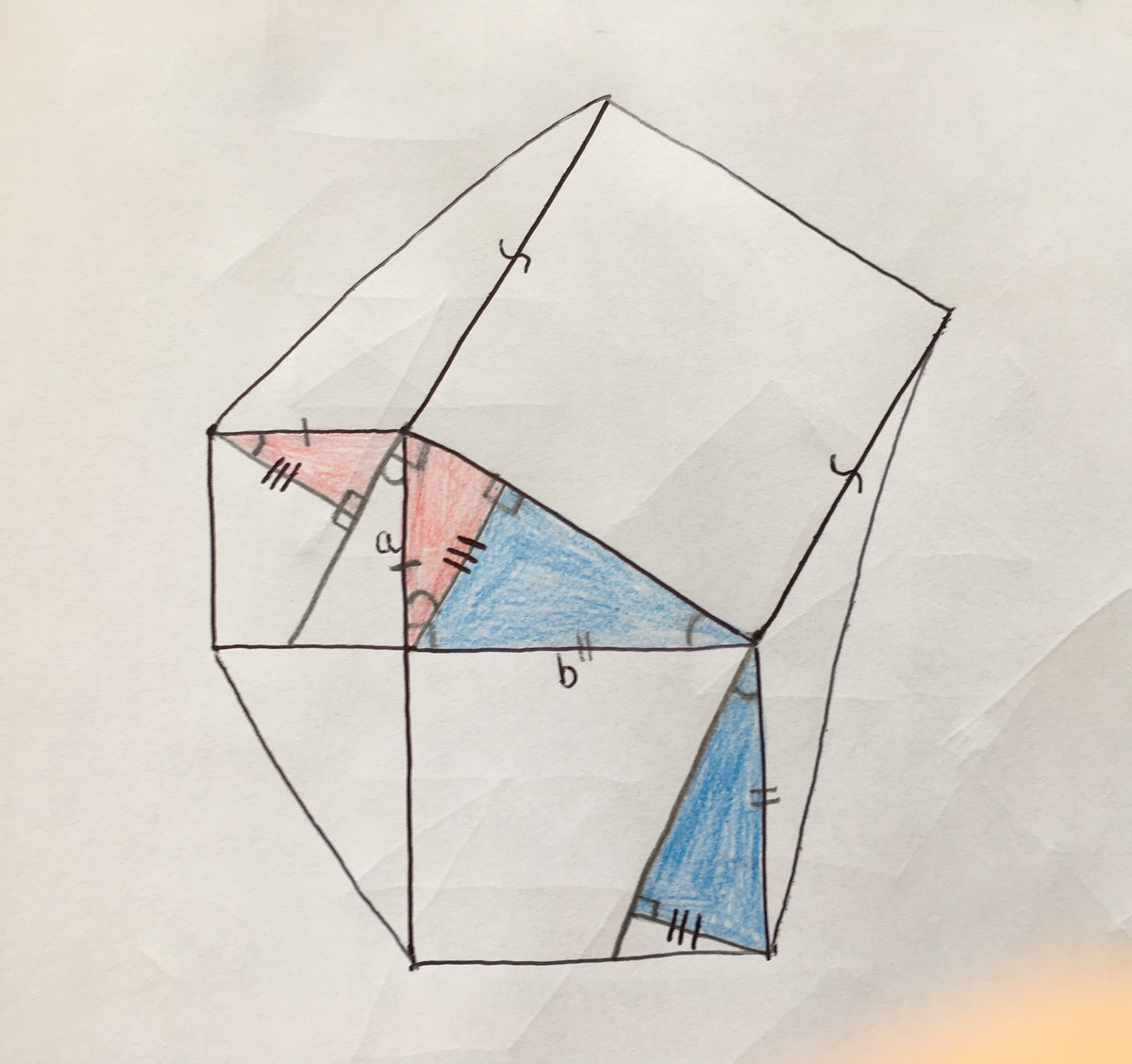 It can easily be shown that the triangle at the bottom is identical to our original one.
It can easily be shown that the triangle at the bottom is identical to our original one.
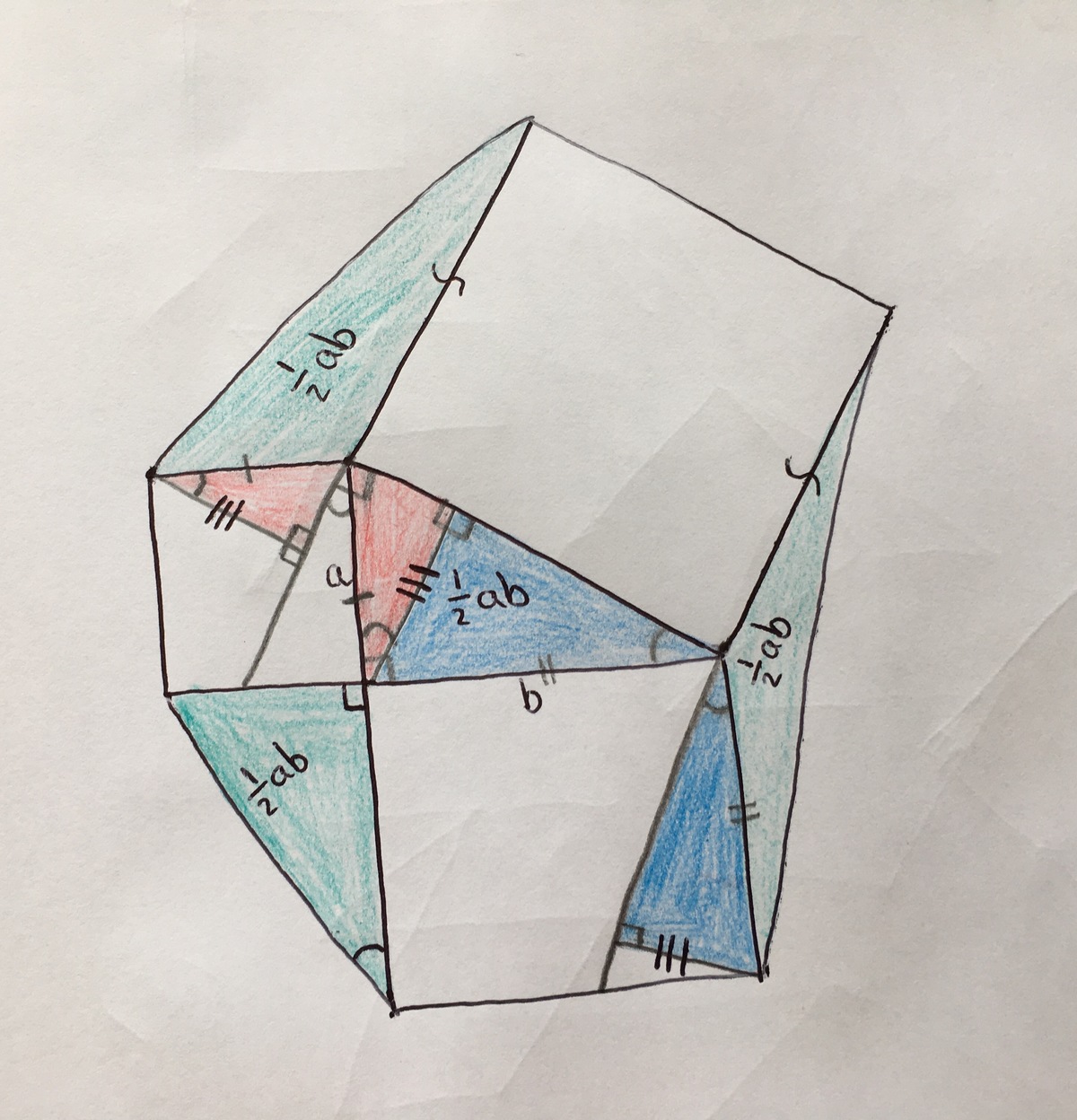
Since the triangles all have the same area, the area of the entire figure will be A = 2 1 a b × 4 + 2 ( a 2 + b 2 ) = 2 a b + 2 ( a 2 + b 2 ) = 2 ( a 2 + a b + b 2 ) .
In this case, we get 7 4 .
Nice one!!. Its pretty evident that you put a lot of effort. Good work and thanks for the solution
Very neat!
If extend the segments of the squares of 3 and 4 we will have the next figure
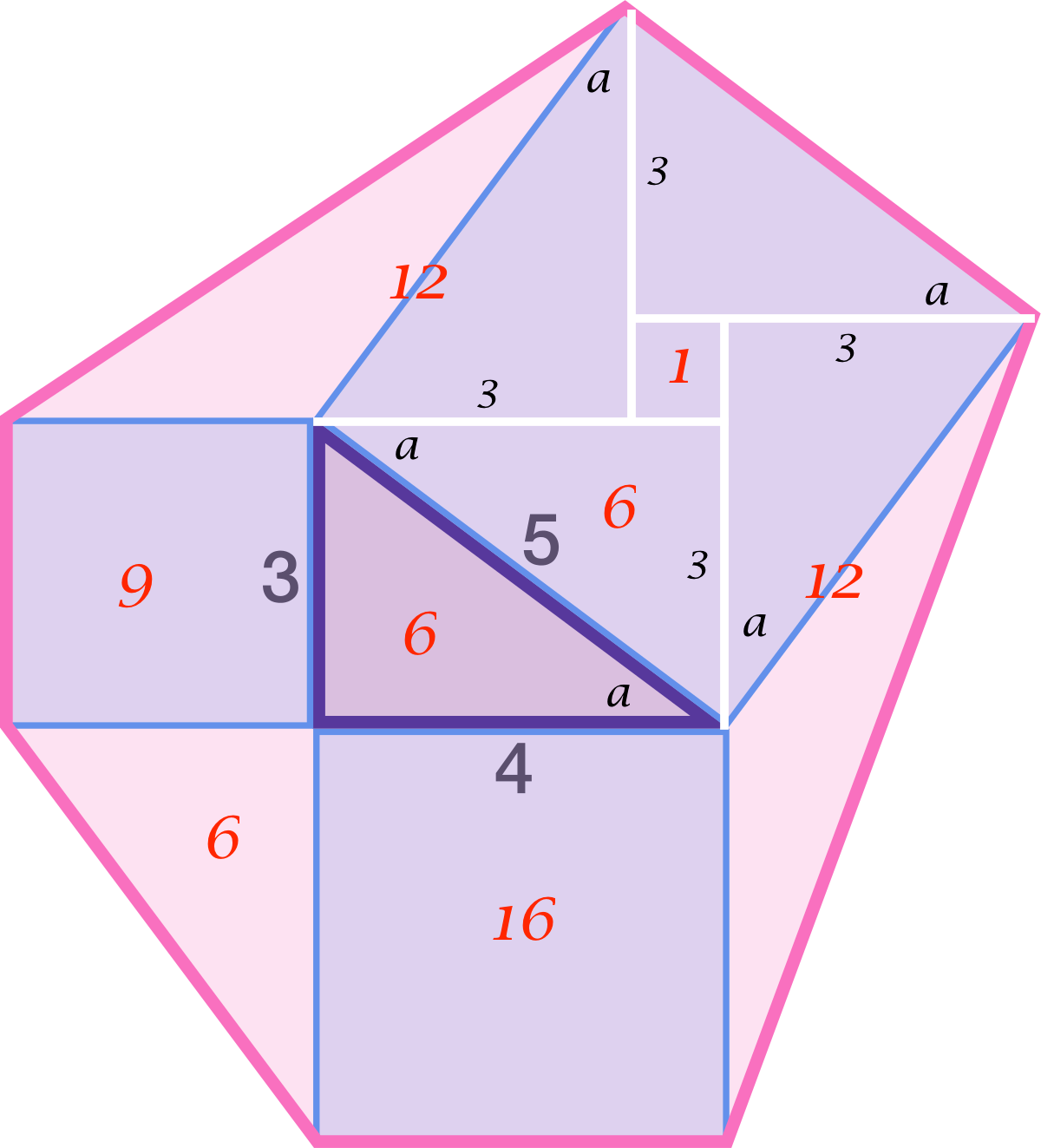
The next is see the measure of some segments of withe and we will get a triangles rectangles also is so easy to calculate the areas and the sum
Red = Areas of triangles
How did you figure out the lengths of the triangle?
Log in to reply
Its easy know the lengths of the triangles because are congruents with 3-4-5 triangle
I calculated the area of the two non right triangles using the length of two sides and the angle to find the length of the third side and then calculated the area from the length of all three sides I did use online calculators for this so in essence I think I cheated
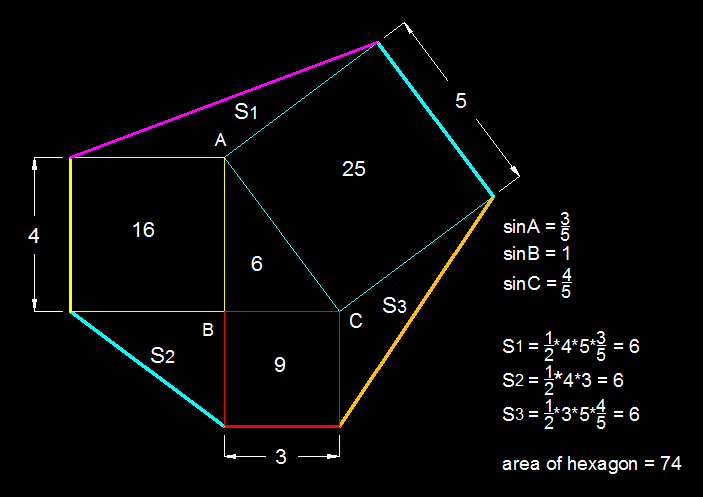
All of the triangles in the diagram have the same area. Therefore the total area is 4 times the area of the central triangle plus the area of the three squares = 4 × ( 2 3 × 4 ) + 4 2 + 3 2 + 5 2 = 7 4 .
Proof: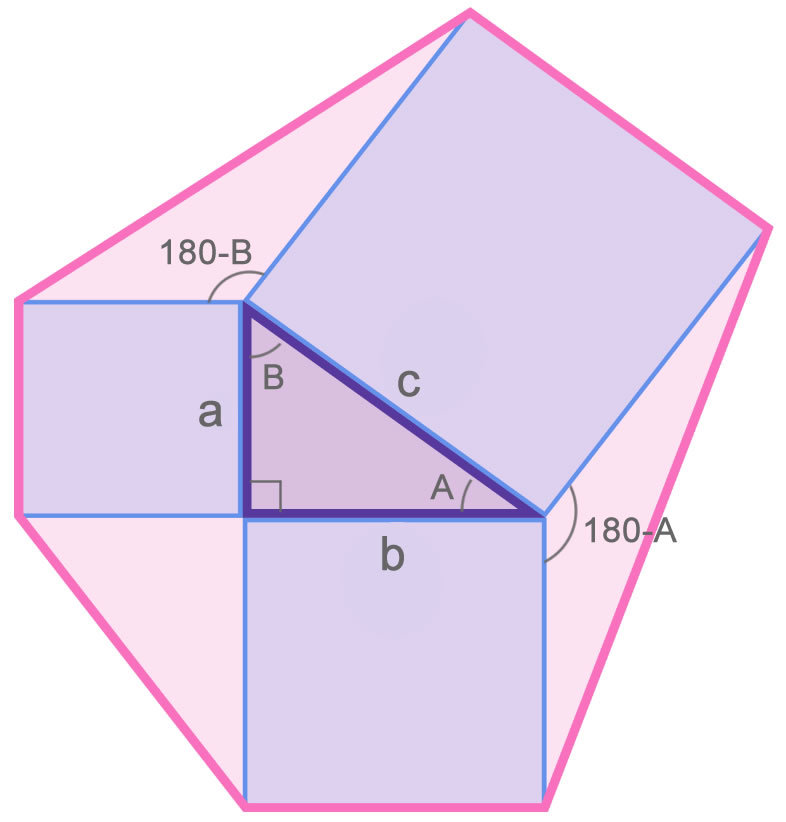 Area of the left-upper triangle is
2
1
a
c
sin
(
1
8
0
−
B
)
.
Area of the left-upper triangle is
2
1
a
c
sin
(
1
8
0
−
B
)
.
Since sin ( 1 8 0 − B ) = sin ( B ) = c b , the area is 2 1 a c c b = 2 1 a b .
By the same logic, the area of the triangle on the right is 2 1 b c sin ( 1 8 0 − A ) = 2 1 b c sin ( A ) = 2 1 b c c a = 2 1 a b .
The area of the left-lower triangle is obviously just 2 1 a b .
Thus, all three triangles have the same area of 2 1 a b .